Example: De-aliasing Factors

Functions > Design of Experiments > Factor Screening > Example: De-aliasing Factors

Use the fractfact, fractresol, fractruns, fractalias, quickscreen, effectsgraph, foldover, and stack functions to screen factors in an experiment that studies the time required for the eye to focus. The factors chosen for the experiment are as follows:

A:	Sharpness of vision
B:	Distance from target to eye
C:	Target shape
D:	Illumination level
E:	Target size
F:	Density
G:	Subject

It is assumed that only a few factors are important, and that high-order interactions between factors can be neglected.

1. Define the number of experiment factors.

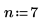
2. Define the fraction power for a fractional factorial design.

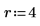
3. Call fractfact to create the design matrix X.

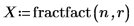
4. Define string gen to record the factors and aliasing of the design matrix X.

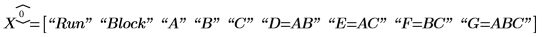
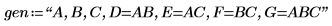
5. Call fractresol and fractruns to find out the resolution and the number of runs of the design matrix X.

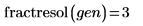
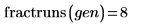
The design matrix X represents an 8-run fractional factorial of resolution III (its main factors are not aliased with one another but they are aliased with second-order interactions).

6. Record the results of the experiment in matrix Y1 with one row per run and one column per replicate.

7. Call the quickscreen function.

8. Call the effectsgraph function and create an effects plot to determine which factors are significant.

<region id="ID0E6K1V" actualWidth="576.40000000000009" actualHeight="288" top="1747.2000000000003" left="38.400000000000006" height="288" width="576.40000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="30">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">effects</traceStyle>
        </trace>
      </traces>
      <graph-size width="476.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-0.25" end="6.25">
          <axisLine position="bottom" positionticmark="-1" legendWidth="104.636666666667" />
          <axisGrid>
            <gridFrequency>21</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Factors</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="80" end="120">
          <axisLine position="left" positionticmark="-1" legendWidth="68.5466666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve">E</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

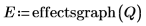
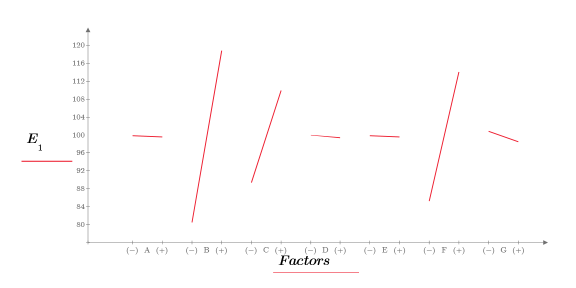
Factors B, C and F display large effects.

9. Call fractalias to find out which second order interactions are aliased with B, C and F.

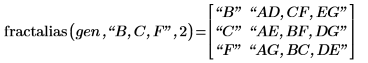
When B and C are significant factors, there is a high probability that the interaction BC is also significant. BC is aliased with F and we do not know if the effect seen for F is caused by F or BC. The same problem occurs for B and F, and for C and F. The main factors and the second order interactions need to be dealiased.

10. Call foldover to fold-over the design matrix X and to break the aliases between main factors and second-order interactions.

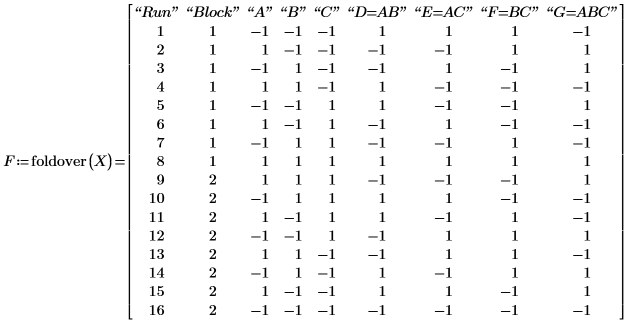
The eight rows of matrix X are inverted in the lower half of F. You can choose specific factors to foldover.

11. Record the results of the additional runs of the folded-over design matrix F.

12. Use function stack to stack the original and the additional runs in matrix Y.

13. Call the quickscreen and effectsgraph functions and create an effects plot to determine the factor effects.

<region id="ID0E5W1V" actualWidth="576.8" actualHeight="312" top="3513.6000000000004" left="38.400000000000006" height="312" width="576.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="37">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">effects</traceStyle>
        </trace>
      </traces>
      <graph-size width="476.8" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-0.25" end="6.25">
          <axisLine position="origin" positionticmark="-1" legendWidth="104.636666666667" />
          <axisGrid>
            <gridFrequency>21</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Factors</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="79.5" end="119.5">
          <axisLine position="origin" positionticmark="-1" legendWidth="76.5266666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve">E1</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

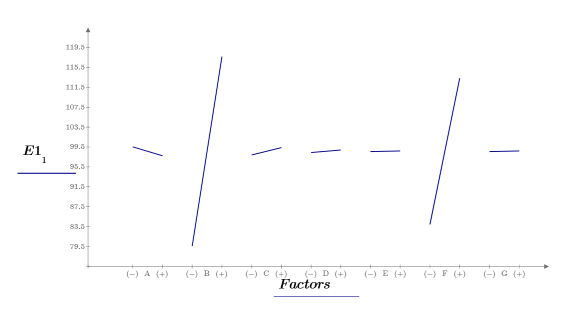
Only factors B and F are significant. The previous effect seen for factor C was therefore due to the BF interaction. You can now carry out further experiments to analyze how factor B (the distance between the target and the eye) and factor F (the density) affect the focus time.

Reference

Montgomery, D.C., Design and Analysis of Experiments, 5th ed, John Wiley & Sons, New York, 2001, pp. 341.