Example: Data Smoothing
Use the movavg, expsmooth, and medsmooth functions to perform a moving average, an exponential windowing, or a median filtering. These functions smooth data by averaging each point in a set of data with itself and neighboring points, reducing irregularities in the data.
Moving Average
For times t = 0, 1, 2, . . . , n - 2 the smoothed value at t is the arithmetic average of all observations up to and including time t. Once n observations have been obtained, the smoothed value at time t is the average of the observation at time t and the previous n - 1 observations.
1. Use the sin function to define a decaying sinusoidal signal.
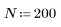
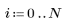
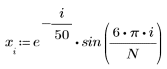
2. Use the rnd function to introduce a uniform but random component to make the signal noisy.
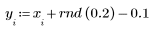
3. Call the movavg function to smooth the data using windows of width 2, 10 and 20, respectively.

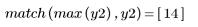
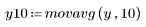
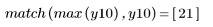
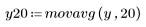
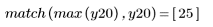
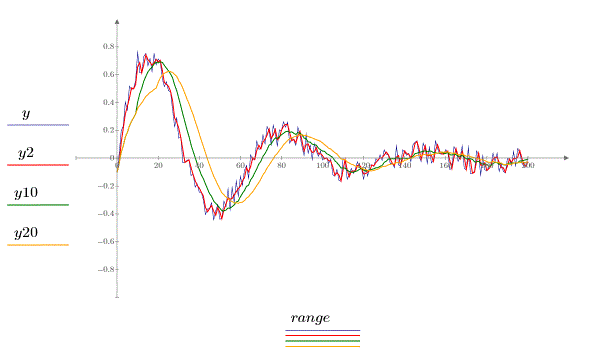
Large window widths introduce a time lag.
Exponential Averaging
Use a step function to illustrate the difference between movavg and expsmooth. Exponential data averaging is computed as follows:
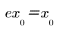
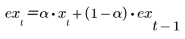
for t = 1, . . . , last(x)
The smoothed entry at time t is the average with weight α of the current observation and the previous smoothed observation.
1. Define and plot a step function.
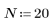 | 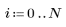 |
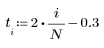 | 0.3 is added to set the function to zero for negative t. |
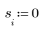 | |
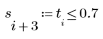 | 0.7 is used instead of 1 to get a pulse with of 1.0. |
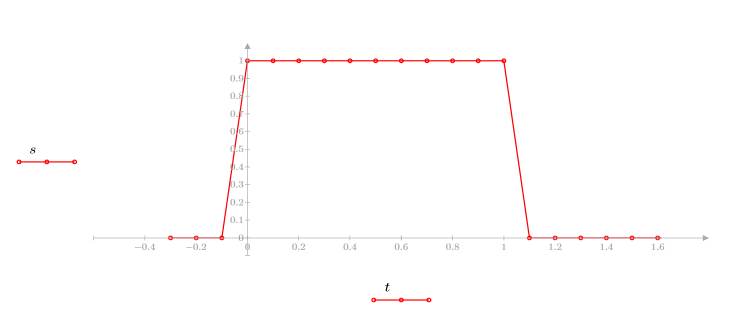
2. Apply the movavg function to the step function using a window width of 4.
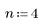
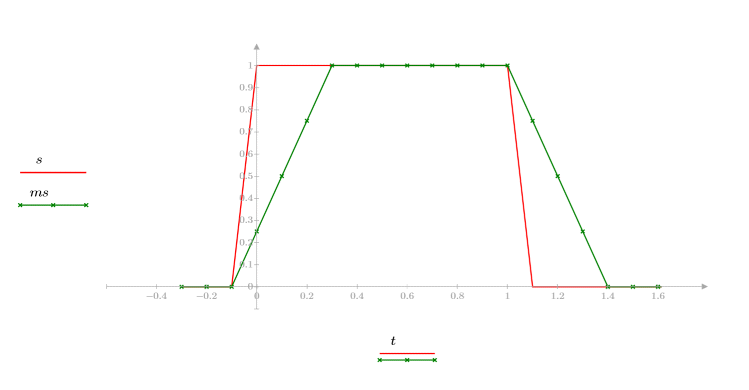
Applying the movavg function to the step function results in smoothing the transition from 1-to-0 in n=4 samples.
3. Apply the expsmooth function to the step function using a weight of 0.5.
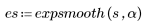
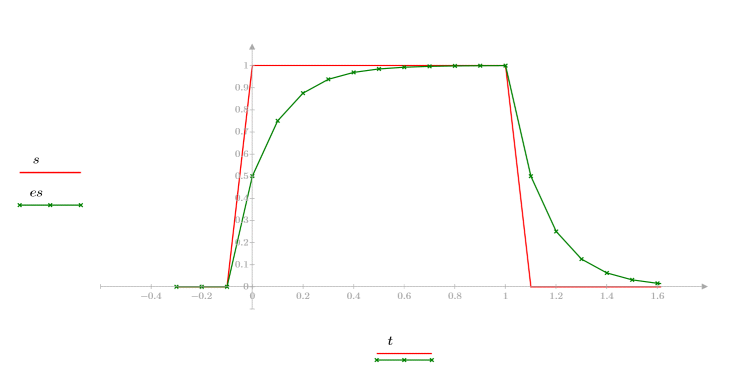
Applying the expsmooth function to the step function results in smoothing the transition from 1-to-0 into a curve in 10 samples.
expsmooth can be used for market trend prediction in the same way as movavg, but in practice most professionals use other indicators, such as the differences between two exponential smoothings, with different weights, of the same raw data.
Median Filtering
Median filtering replaces each element of the input with the median of the element and n-1 of its neighbors or fewer near the ends of the signal. This method is good for smoothing while maintaining edges and for noise reduction.
On large matrices, the function takes more time because it performs a sort at each pixel. Besides removing the noise, median filtering tends to remove sharp, small transients from a signal.
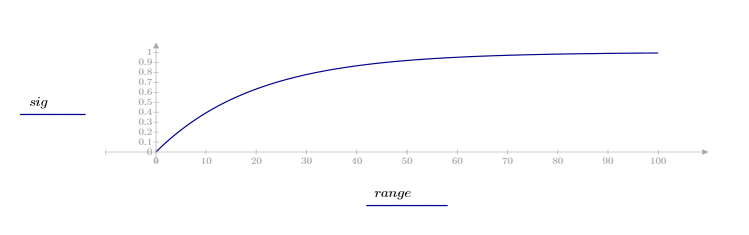
1. Define and plot an exponential signal.
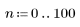
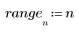
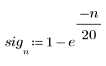
2. Use the whiten function to degrade the quality of the signal by adding some random white noise.
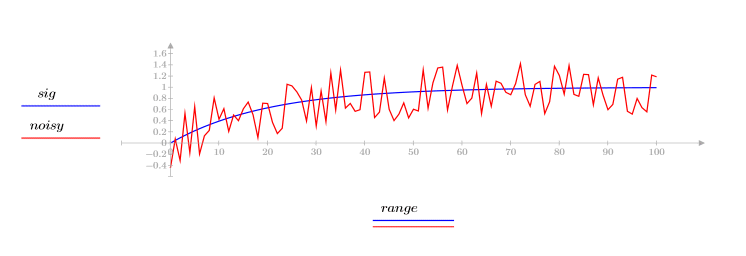
3. Use the medsmooth function to apply a median filter, and then plot the filtered signal.
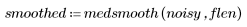
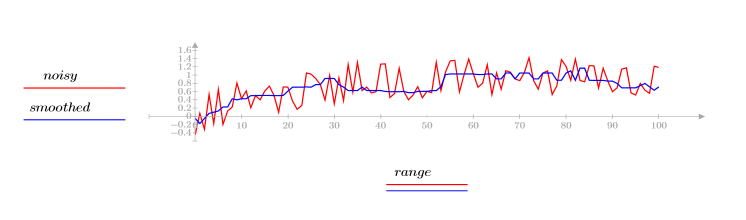
The filtered version of the signal is smoother.
Change the length of the filter to see its effect on the noisy signal. In practice, the length of the median filter should be small compared to the length of the signal.