Example: Cauchy Distribution

Functions > Statistics > Probability Distributions > Example: Cauchy Distribution

1. Show the definition of the Cauchy distribution:

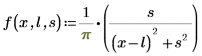
Where:

◦ l is the location parameter (mean)

◦ s is the scale parameter (square-root of variance), s > 0

2. Define three sets of location and scale parameters, then calculate the amplitude, or height, of the curve with location and scale parameters l0 and s0:

<region id="ID0EM6RBB" top="307.20000000000005" left="38.400000000000006" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="239"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>0</real> </define> </math> </region>	<region id="ID0EBASBB" top="307.20000000000005" left="115.20000000000002" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="241"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> </math> </region>	<region id="ID0EWASBB" top="307.20000000000005" left="211.20000000000005" height="27.791200000000003" width="53.826666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="243"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>-2</real> </define> </math> </region>
<region id="ID0EOBSBB" top="268.80000000000007" left="38.400000000000006" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="233"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>1</real> </define> </math> </region>	<region id="ID0ECCSBB" top="268.80000000000007" left="115.20000000000002" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="235"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>1</real> </define> </math> </region>	<region id="ID0EWCSBB" top="268.80000000000007" left="211.20000000000005" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="237"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>1</real> </define> </math> </region>

<region id="ID0EIDSBB" top="364.80000000000007" left="38.400000000000006" height="49.391200000000005" width="170.46666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="245">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <eval>
 <apply>
 <div />
 <real>1</real>
 <apply>
 <mult />
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
</region>

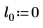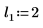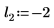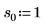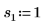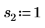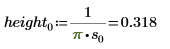
3. Use the dcauchy function to get the probability density for value x using different values of location parameters and a fixed scale parameter:

<region id="ID0ELFSBB" top="460.80000000000007" left="38.400000000000006" height="307.19999999999993" width="556.4000000000002" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="247">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="248">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="DashDot">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="249">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="360.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="250">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="251">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.33">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="252" display="true" color="#FFED1D2F" line-style="Dash" value="0.31830988618379069">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="254">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="255">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="256">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="257">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="258">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="259">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

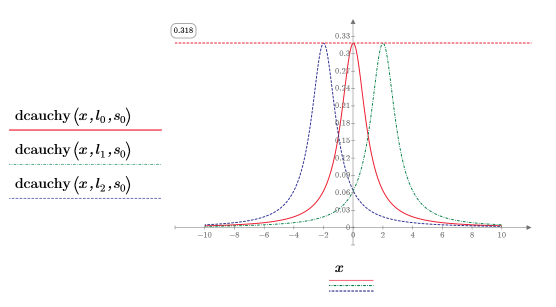
Different values of location parameters shift the curve along the x-axis.

4. Plot the dcauchy function using a fixed location parameter and different values of scale parameters:

<region id="ID0ELISBB" top="940.80000000000018" left="38.400000000000006" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="275"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EAJSBB" top="940.80000000000018" left="115.20000000000002" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="277"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EVJSBB" top="940.80000000000018" left="192.00000000000003" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="279"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0ENKSBB" top="902.40000000000009" left="38.400000000000006" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="269"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>1</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EBLSBB" top="902.40000000000009" left="115.20000000000002" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="271"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EVLSBB" top="902.40000000000009" left="192.00000000000003" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="273"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>3</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

<region id="ID0EHMSBB" top="998.40000000000009" left="38.400000000000006" height="49.391200000000005" width="170.46666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="281">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <eval>
 <apply>
 <div />
 <real>1</real>
 <apply>
 <mult />
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0EVMSBB" top="1036.8000000000002" left="38.400000000000006" height="307.2" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="283">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="284">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="285">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="286">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="287">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.33">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="288" display="true" color="#FF068149" line-style="Dash" value="0.15915494309189535">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="290">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="291">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="292">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="293">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="294">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="295">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

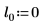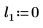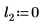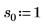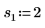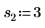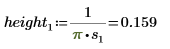
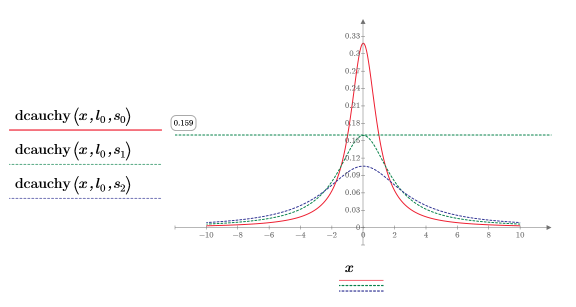
Different values of scale parameters change the height of the curve.

5. Plot the dcauchy function using different values of location parameters and scale parameters:

<region id="ID0EVPSBB" top="1497.6000000000001" left="38.400000000000006" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="311"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EKQSBB" top="1497.6000000000001" left="115.20000000000002" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="313"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E6QSBB" top="1497.6000000000001" left="192.00000000000003" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="315"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>4</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EXRSBB" top="1459.2000000000003" left="38.400000000000006" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="305"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>1</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ELSSBB" top="1459.2000000000003" left="115.20000000000002" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="307"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E6SSBB" top="1459.2000000000003" left="192.00000000000003" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="309"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>3</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

<region id="ID0ERTSBB" top="1555.2000000000003" left="38.400000000000006" height="49.391200000000005" width="170.46666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="317">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <eval>
 <apply>
 <div />
 <real>1</real>
 <apply>
 <mult />
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0E6TSBB" top="1747.2000000000003" left="38.400000000000006" height="307.2" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="319">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="320">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="321">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="322">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="323">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.33">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="324" display="true" color="#FF2E3192" line-style="Dash" value="0.1061032953945969">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="326">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="327">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="328">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="329">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="330">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="331">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

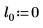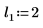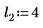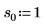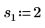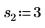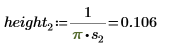
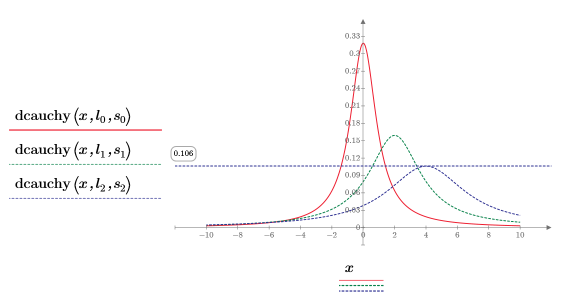
Different values of scale and location parameters shift the curves and change their height.

6. Plot the pcauchy function using different values of location parameters and a fixed scale parameter:

<region id="ID0ECWSBB" top="2169.6000000000004" left="38.400000000000006" height="326.4" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="341">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="342">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="343">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="249.6" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="344">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="345">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="1">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>6</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker display="true" color="#FF000000" line-style="Dash" value="1" />
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="352">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="353">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="354">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="355">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="356">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="357">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="347">
 <real xmlns="http://schemas.mathsoft.com/math50">0.0</real>
 </startValue>
 <secondTickValue resultRef="349">
 <real xmlns="http://schemas.mathsoft.com/math50">0.2</real>
 </secondTickValue>
 <endValue resultRef="351">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

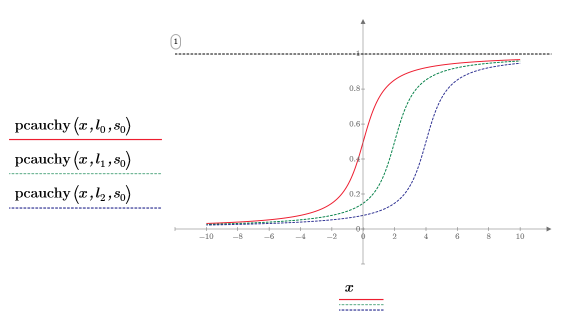
◦ Different values of location parameters shift the curve along the x-axis.

◦ All y values of pcauchy are between 0 and 1.

7. Plot the pcauchy function using a fixed location parameter and different values of scale parameters:

<region id="ID0EC2SBB" top="2668.8" left="38.400000000000006" height="326.4" width="575.6" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="373">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="374">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="375">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="379.6" height="249.6" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="376">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="377">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="1">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>6</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="378" display="true" color="#FF000000" line-style="Dash" value="0.5">
 <real xmlns="http://schemas.mathsoft.com/math50">0.5</real>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="386">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="387">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="388">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="389">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="390">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="391">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="381">
 <real xmlns="http://schemas.mathsoft.com/math50">0.0</real>
 </startValue>
 <secondTickValue resultRef="383">
 <real xmlns="http://schemas.mathsoft.com/math50">0.2</real>
 </secondTickValue>
 <endValue resultRef="385">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

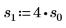
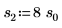
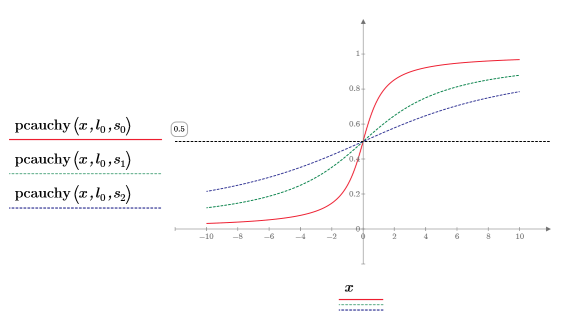
◦ Different values of scale parameters flatten the curve horizontally, but all curves cross at y=0.5.

◦ All y values of pcauchy fall between 0 and 1.

8. Plot the qcauchy function using different values of location parameters and a fixed scale parameter:

<region id="ID0EV6SBB" top="3110.4000000000005" left="38.400000000000006" height="326.4" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="404">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="405">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="406">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="249.6" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-1" end="1">
 <axisLine position="origin" positionticmark="3" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker display="true" color="#FF000000" line-style="Dash" value="1" />
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="411">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="412">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="408">
 <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
 </startValue>
 <endValue resultRef="410">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-15" end="15">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>7</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="419">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">qcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="420">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="421">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">qcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="422">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="423">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">qcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="424">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="414">
 <real xmlns="http://schemas.mathsoft.com/math50">-15</real>
 </startValue>
 <secondTickValue resultRef="416">
 <real xmlns="http://schemas.mathsoft.com/math50">-10</real>
 </secondTickValue>
 <endValue resultRef="418">
 <real xmlns="http://schemas.mathsoft.com/math50">15</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

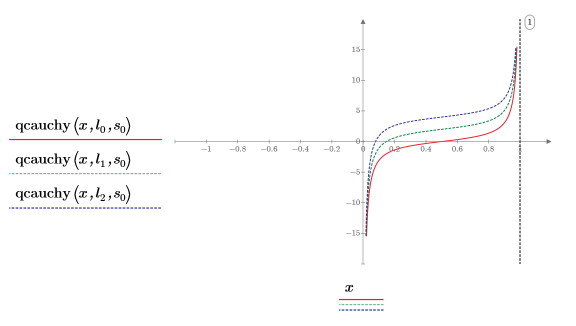
◦ Different values of location parameters shift the curve along the y-axis.

◦ All x values of qcauchy fall between 0 and 1.

9. Calculate the rcauchy function using fixed location and scale parameters:

<region id="ID0E3ETBB" top="3648.0000000000005" left="38.400000000000006" height="27.791200000000003" width="169.31666666666666" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="442">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">R</id>
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rcauchy</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </parens>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="true" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

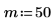
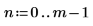
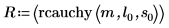
Function rcauchy returns a vector of m random numbers having the Cauchy distribution.

10. Plot the random numbers returned by the rcauchy function.

<region id="ID0E5GTBB" top="3744.0000000000005" left="38.400000000000006" height="288" width="576.39999999999986" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="444">
 <traceStyle color="#FFED1D2F" symbol="filledStar" line-weight="2" line-style="None">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="476.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="50">
 <axisLine position="origin" positionticmark="6" legendWidth="61.7533333333333" />
 <axisGrid>
 <gridFrequency>6</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="451">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">n</id>
 </math>
 <math resultRef="452">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="446">
 <real xmlns="http://schemas.mathsoft.com/math50">0</real>
 </startValue>
 <secondTickValue resultRef="448">
 <real xmlns="http://schemas.mathsoft.com/math50">10</real>
 </secondTickValue>
 <endValue resultRef="450">
 <real xmlns="http://schemas.mathsoft.com/math50">50</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-12" end="8">
 <axisLine position="origin" positionticmark="0" legendWidth="69.59" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="453">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">R</id>
 <id xml:space="preserve">n</id>
 </apply>
 </math>
 <math resultRef="454">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

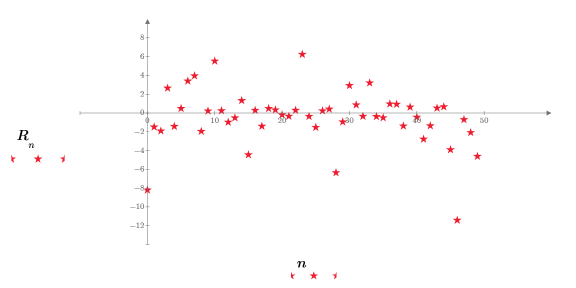
Recalculating the worksheet causes function rcauchy to return a new set of random numbers, and the plot gets updated accordingly.