Example: Calculating Effects

Functions > Design of Experiments > Factor Screening > Example: Calculating Effects

Use the quickscreen and effects functions to calculate the effects of factors, factor levels, blocking, and interactions in design experiments.

1. Call the fullfact function to create a design matrix to test the nickel plating process used to manufacture high-technology disks for computer disk drives. Factor A stands for the process temperature (16°C and 32°C) and factor B stands for the process time (4s and 12s).

2. Call the block function to divide the design matrix into two blocks to carry out the experiment in two separate labs.

You can also choose a specific factor or interaction to block:

3. Record the thickness readings in matrix Y with one row per run and one column per replicate.

For later reference, use the mean function to define r1, r2, r3, and r4 to be the average thickness reading for each run.

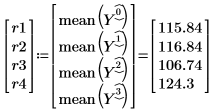
Effects of Factors

1. Call the quickscreen function to calculate the effect of each factor.

<region id="ID0EEFQV" actualWidth="499.4666666666667" actualHeight="81.4" top="1132.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="33">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Q</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">quickscreen</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

According to the blocked design matrix K, factor A is at its low level for "Run 2" and "Run 3", and at its high level for "Run 1" and "Run 4”.

2. Calculate the low average response (lar) and the high average response (har) for the process temperature factor A.

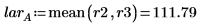
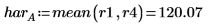
3. Calculate the temperature effect (te) defined as the difference between the high and the low average responses of factor A.

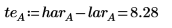
4. Compare the results returned by the quickscreen function for factor A with the above calculated results.

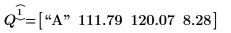
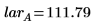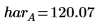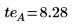5. Use the effects function to calculate the effect of each factor level.

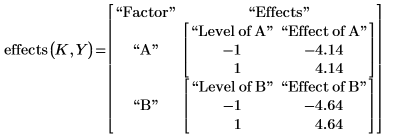
The effects of the factor levels are calculated about the overall mean of the results:

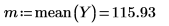
6. Calculate the effect returned for the low and high levels of factor A.

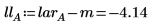
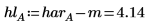
The difference between the low level effect and the high level effect is the factor effect calculated by the quickscreen function. This is true for factors having two levels only.

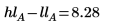
Effect of Blocking

1. Add a third argument to the effects function to calculate the blocking effect.

<region id="ID0EMWQV" actualWidth="320.91333333333336" actualHeight="62.800000000000004" top="2304.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="47">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">effects</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <str xml:space="preserve">Blocks</str>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

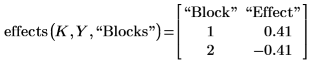
The block number is defined in the "Block" column of the design matrix K.

2. Calculate the blocking effect.

The blocking effect is calculated in the same way as the level effects of factor A above.

For "Block 1", take the difference between the mean of the first two rows and the overall mean of the results:

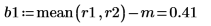
For "Block 2", take the difference between the mean of the last two rows and the overall mean of the results:

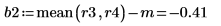
The difference between the "Block 1" and the "Block 2" effects is the blocking effect calculated by the quickscreen function. This is true for design matrices having two blocks only.

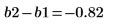
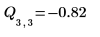
Effects of Interactions

1. Add a third argument to the quickscreen function to view the effect of interaction AB.

<region id="ID0EE4QV" actualWidth="515.66333333333341" actualHeight="44.2" top="2803.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="52">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">quickscreen</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <str xml:space="preserve">AB</str>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

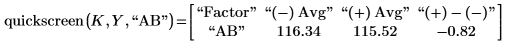
For each run, the levels of interaction AB are determined by the product of the levels of A and B. For "Run 1", the levels of A and B are -1 and 1, therefore the level of AB is -1.

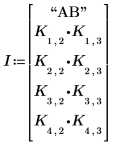
2. Change the third argument of the effects function to view the level effect of interaction AB.

Reference

Schmidt, S. and Launsby, R., Understanding Industrial Designed Experiments, Colorado Springs: Air Academy Press & Associates, 1994, pp. 2–8.