Example: ANOVA and Blocking

Functions > Design of Experiments > Factor Screening > Example: ANOVA and Blocking

Use the block and anova functions to divide a design matrix into two blocks and to test if the blocking has an effect on the result.

1. Call the fullfact function to create a full factorial design matrix.

2. Call the block function to divide the design matrix X into two blocks.

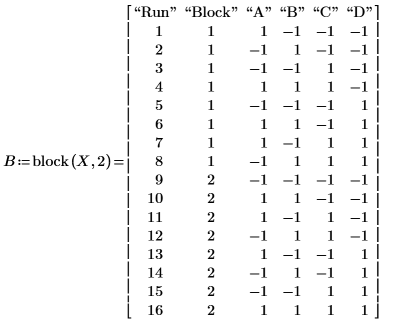
The first eight runs are in Block 1 and the remaining runs are in Block 2.

3. Call the randomize function before carrying out the experiment. The randomization is carried out separately for each block.

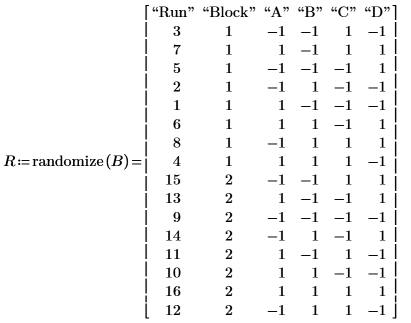
4. Record the experiment results in matrix Y with one row per run of the blocked design matrix B and one column per replicate.

5. Call the quickscreen function to calculate the effects of the factors, the second order interactions and the blocking.

<region id="ID0EUHWV" actualWidth="515.54" actualHeight="230.19999999999996" top="1862.4000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">Q</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">quickscreen</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
            <real>2</real>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="17,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

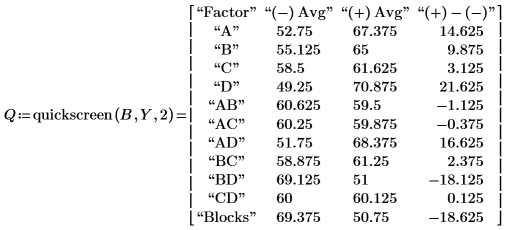
6. Use the augment and submatrix functions to extract the factors and their effects from Q, and remove the headers.

<region id="ID0EMKWV" actualWidth="182.82" actualHeight="29.752000000000002" top="2054.4" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="54">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">data</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">augment</id>
        <sequence>
          <apply>
            <matcol />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q</id>
            <real>0</real>
          </apply>
          <apply>
            <matcol />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q</id>
            <real>3</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="17,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E1KWV" actualWidth="489.85" actualHeight="211.59999999999997" top="2188.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="56">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">data</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">submatrix</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">data</id>
            <real>1</real>
            <apply>
              <minus />
              <apply>
                <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">data</id>
              </apply>
              <real>1</real>
            </apply>
            <real>0</real>
            <real>1</real>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
  </math>
</region>

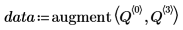
7. Replace the effects by the absolute value of the half effects.

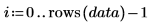
8. Call the pareto function and then create a Pareto plot.

<region id="ID0EFPWV" actualWidth="575.61538461538453" actualHeight="360" top="2860.8000000000006" left="38.400000000000006" height="360" width="575.61538461538453" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="64">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="65">
          <traceStyle color="#FF008000" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="422.015384615385" height="283.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="10">
          <axisLine position="origin" positionticmark="0" legendWidth="73.44" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="66">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="67">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="100">
          <axisLine position="left" positionticmark="-1" legendWidth="123.046666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="68">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="69">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <div />
                  <apply>
                    <summation />
                    <lambda>
                      <boundVars>
                        <placeholder />
                      </boundVars>
                      <apply>
                        <matcol />
                        <id xml:space="preserve">P</id>
                        <real>1</real>
                      </apply>
                    </lambda>
                    <upperBound>
                      <placeholder />
                    </upperBound>
                  </apply>
                  <real>100</real>
                </apply>
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="70">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P</id>
                  <real>2</real>
                </apply>
              </math>
              <math resultRef="71">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

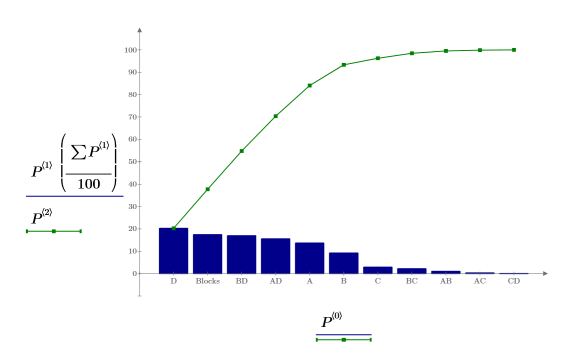
Factors A, B, D, interactions AD and BD, and Blocks seem significant.

9. Call the anova function to carry out an analysis of variance. Calculate the critical F-value for the factors, interactions, and blocking. Compare their F-value to the critical F-value.

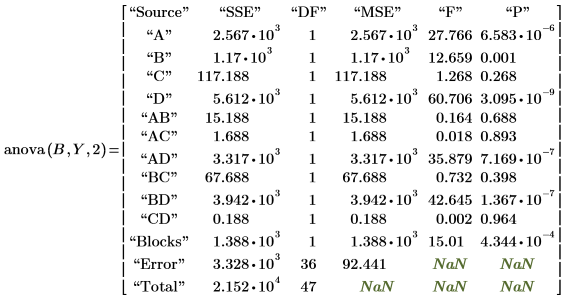
10. Use the qF function to calculate the critical F-value for the factors, interactions, and blocking. Compare their F-value to the critical F-value.

Set the level at 5%:	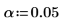<region id="ID0E5VWV" actualWidth="62.706666666666671" actualHeight="25.6" top="3878.4000000000005" left="326.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="80"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">α</id> <real>0.05</real> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="17,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Set the lowest degree of freedom DF:	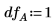<region id="ID0EAXWV" actualWidth="56.150000000000006" actualHeight="27.791200000000003" top="3916.8000000000006" left="326.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="82"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">df<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">A</Subscript></Span> </id> <real>1</real> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="17,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
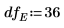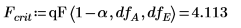Set the highest degree of freedom DF:	<region id="ID0ECYWV" actualWidth="64.233333333333348" actualHeight="27.791200000000003" top="3955.2000000000007" left="326.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="84"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">df<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">E</Subscript></Span> </id> <real>36</real> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="17,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EWYWV" actualWidth="241.32000000000002" actualHeight="27.791200000000003" top="3993.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="86"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">F<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">crit</Subscript></Span> </id> <eval> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">qF</id> <sequence> <apply> <minus /> <real>1</real> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">df<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">A</Subscript></Span> </id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">df<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">E</Subscript></Span> </id> </sequence> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="17,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

Factors A, B, D, interactions AD and BD, and Blocks are significant at the 5% level since their F values are greater than Fcrit. This analysis of variance reinforces the subjective conclusion derived from the Pareto plot.

Reference

Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 295.