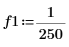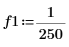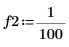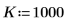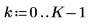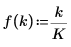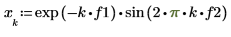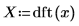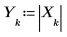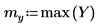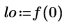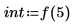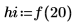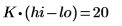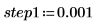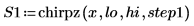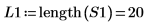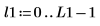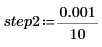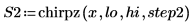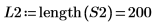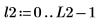例: チャープ-z 変換
チャープ z 変換は、サンプル信号を引数としてとり、小さな周波数区間を等間隔の周波数値で補間したスペクトルを返します。
使用されるチャープ Z 変換アルゴリズムについては、Samuel Stearns and Ruth David, Signal Processing Algorithms (Prentice-Hall, Inc.) に解説があります。
信号の作成
1. 信号周波数を定義します。
2.
exp関数と
sin関数を使用して、減衰正弦波信号を定義します。
減衰正弦波信号は、時間の経過とともにゼロに減衰する指数関数と正弦波関数の積です。
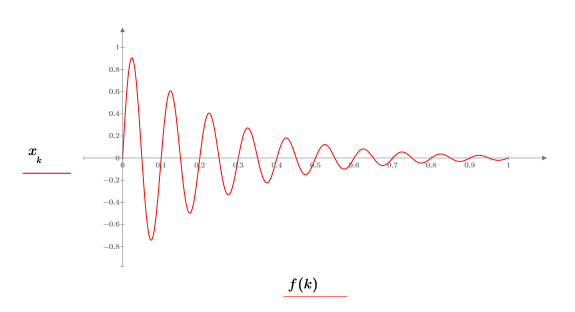
3. 減衰信号をプロットします。
1 がサンプリング周波数を表すように周波数が正規化されています。
4.
dft関数を使用して、この信号の
DFT を求めます。
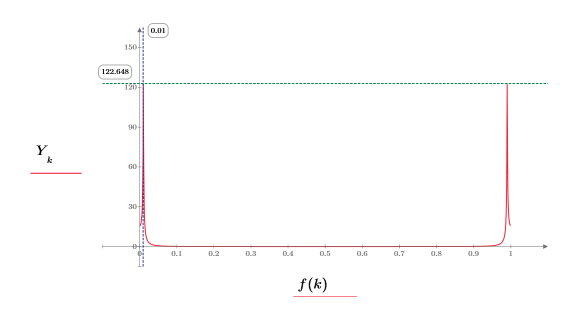
5. 信号の DFT をプロットします。縦マーカーを使用して、1 つ目のピークの大きさと周波数を示します。
指数のスペクトルによってコンボリューションされた正弦波の周波数でピークが発生しています。
6. x 軸方向の周波数スケールを拡大して、1 つ目のピークにズームインします。
7. 周波数範囲内にあるデータ点の数を計算します。
chirpz
chirpz関数を使用してデータ点の数を増やし、ピーク付近のスペクトルを拡大します。
1. ステップパラメータを設定し、chirpz 関数を使用してスペクトルを計算します。
2. 補間されたスペクトル内の点の数を計算します。
3. 新しいレンジを使用して、DFT の 1 つ目のピークに補間されたスペクトルを重ね合わせます。
0.001 のステップで、chirp-z トレースに同じ数のデータ点が返されるため、2 つのトレースは同一に見えます。
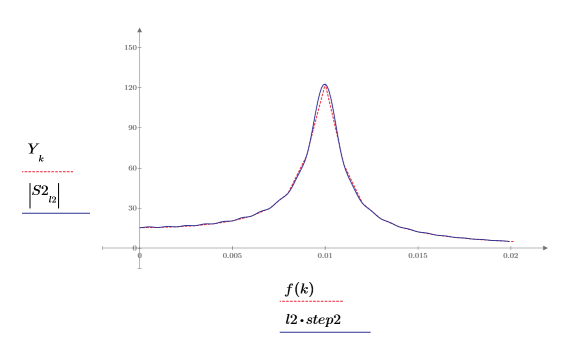
4. ステップサイズを 1/10 に縮小してから、2 つの関数をもう一度計算およびプロットします。
5. 補間されたスペクトル内の新しい点の数を計算します。
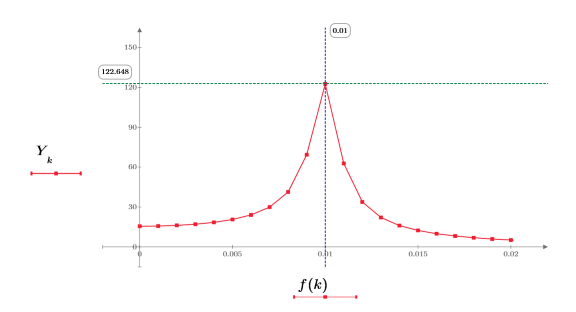
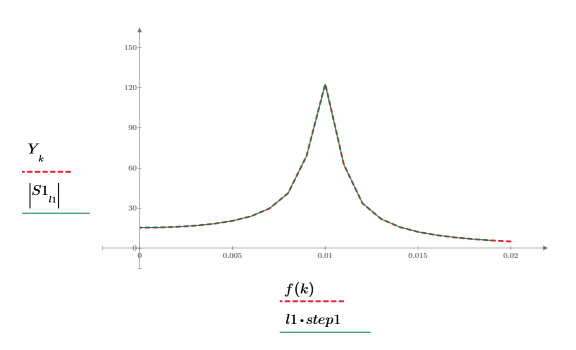
6. DFT の 1 つ目のピークと新しく補間したスペクトルを重ね合わせます。
このプロットは、補間された点の数が増えるほど、ピーク付近のスペクトルトレースが丸みを帯びることを示しています。
7. step2 をさらに 1/10 に縮小し、上記プロットに対する影響を確認します。