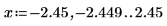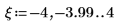例: 制約条件があるソルブブロック
ソルブブロックを使用して、制約条件がある連立方程式の解を求めます。
円と直線の交点を考えます。制約条件がなく、複数の解が存在する場合は、推定値によってどの解が見つかるかが決まります。
1. ソルブブロックを挿入して、推定値と制約条件を定義した後、
findソルバー関数を使用して直線と円の交点を求めます。
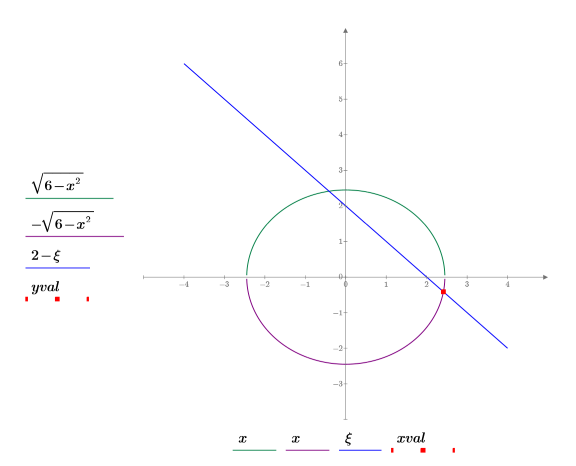
2. 円、直線、交点をプロットします。
プロットから、この解は、2 つの交点のうちの推定値に近い方の点であることがわかります。
3. 推定値を変えて解を再計算します。
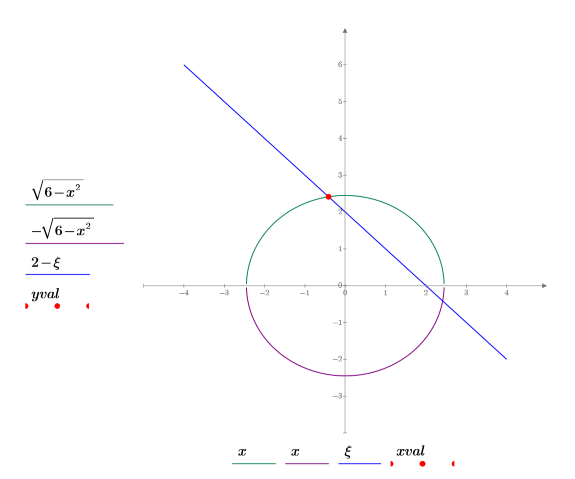
4. 円、直線、交点をプロットします。
プロットから、新しい推定値に近い方の点が選択された結果、2 つ目の交点が解であることがわかります。
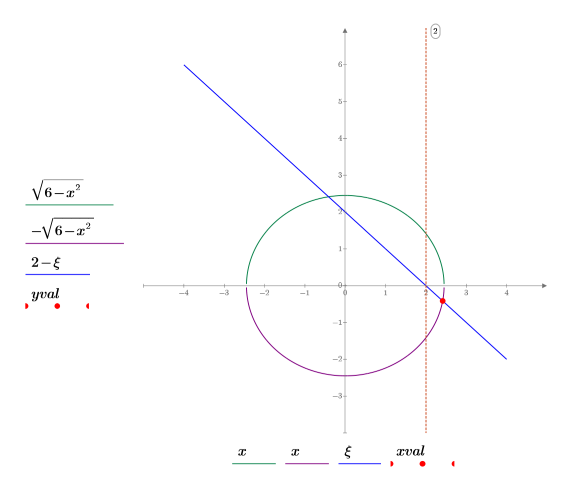
5. x > a (ここで a は定数) の形式で制約条件を追加します。これによって、直線 a の左側の領域は除外されます。
6. 円、直線、交点をプロットします。垂直マーカーを使用して直線 a を示します。
プロットから、新しい制約条件を満たすため、唯一とりうる可能な 1 つ目の交点が解であることがわかります。