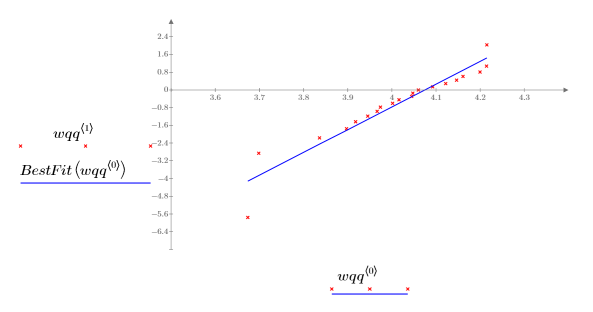
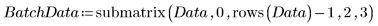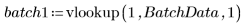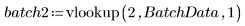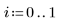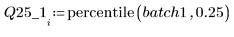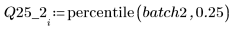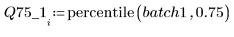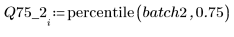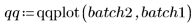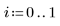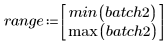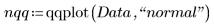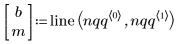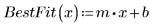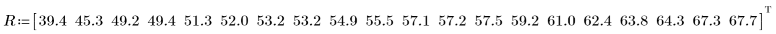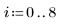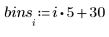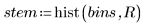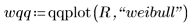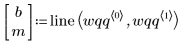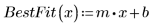例: 分位-分位プロット
qqplot関数を使用して分位-分位 (Q-Q) プロットを作成します。
2 つのデータセット
Q-Q プロットで 2 つのデータセットの分位を比較し、分布が同じであるかどうかを検定します。
1. データセットを定義します。
列 2 は測定が行われたバッチを示し、列 3 は積層窒化ケイ素の棒材の強度の測定値を示しています。
2. 対象となる列 2 と列 3 を抽出します。
3.
vlookupを呼び出して、測定がバッチ 1 とバッチ 2 のどちらで行われたかに応じてデータを分割します。
4. 各バッチの第 1 四分位と第 3 四分位を計算します。
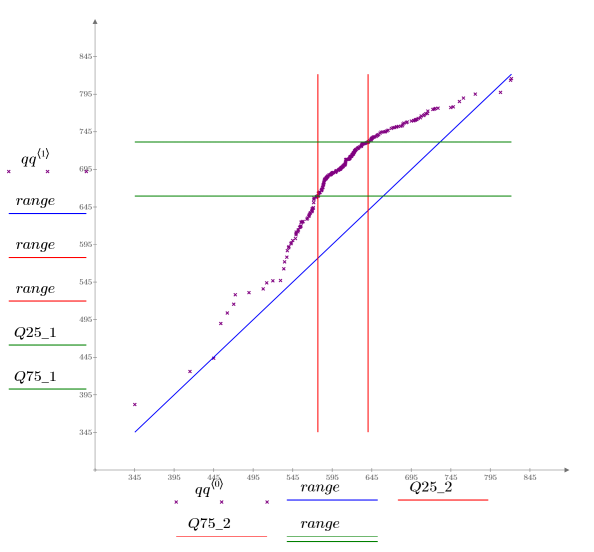
5. Q-Q プロットと分位をプロットします。
データの変化を強調するため、1 対 1 の参照線がプロットされています。
Q-Q プロットから、非常に小さいパーセンタイルの値と非常に大きいパーセンタイルの値はほぼ同じですが、2 つのバッチの分布は異なることがわかります。バッチ 1 の分位はバッチ 2 の分位よりもかなり大きく、これは処理条件がまったく異なることを示唆しています。
正規分布
熱流測定器の測定値がランダムに抽出されているかどうかを調べます。Q-Q プロットで正規分布と比較することで、測定値が正規分布しているかどうかを調べます。
1. 熱流を表すデータセットを定義します。
2. 正規 Q-Q プロットのデータ点を求めます。
3. データの分位が正規分布の分位にどれだけ近いかを示す最良適合の直線を求めます。
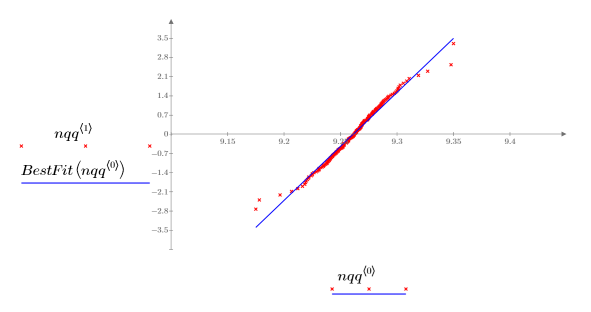
4. Q-Q プロットと最良適合の直線をプロットします。
参照線との間に非常に近い相関があることから、標本は正規分布していることがわかります。
正規性のチェックは、外れ値を検出する場合に行う検定の 1 つです。
ワイブル分布
データセットがワイブル分布に従っているかどうかを検定します。
1. ベクトル R に、徐々に大きな電圧負荷を加えてケーブルの電気絶縁破壊電圧を記録します。
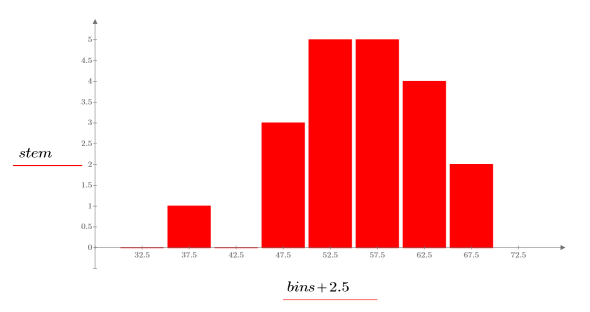
2. データのヒストグラムをプロットします。
ヒストグラムから、データは正規分布していないことがわかります。データは片側に歪んでいます。Q-Q プロットでこのデータをワイブル分布と比較できます。
3. ワイブル Q-Q プロットのデータ点を求めます。
4. データの分位がワイブル分布の分位にどれだけ近いかを示す最良適合の直線を求めます。
5. Q-Q プロットと最良適合の直線をプロットします。
参照線との間に非常に近い相関があることから、このデータセットはワイブル分布によってモデル化可能であることがわかります。
| ワイブル Q-Q プロットでは、対数スケールが使用されます。 |
参考文献
Lawless, J.F., Statistical Methods for Lifetime Data、第 2 版、Wiley-Interscience (2002 年)