例: QR 行列の因子分解

• ブール比較実行時の論理不一致を避けるには、「計算オプション」ドロップダウンリストの「近似等価」を有効にします。

• 例では複素行列を入力として使用していますが、関数には入力として実数行列を使用することもできます。

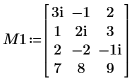
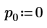
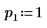
デフォルト関数 QR(M1) は QR(M,1). と等価です。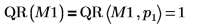

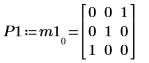
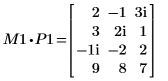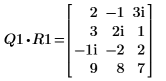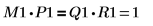<region id="ID0EN1XMB" actualWidth="167.83666666666665" actualHeight="81.4" top="1209.6000000000001" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="16" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M1</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">P1</id> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EA2XMB" actualWidth="165.74" actualHeight="81.4" top="1209.6000000000001" left="211.20000000000005" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="18" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q1</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R1</id> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
<region id="ID0EX2XMB" actualWidth="153.23666666666668" actualHeight="25.6" top="1286.4" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="20" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <equal xml:lang="ja" /> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M1</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">P1</id> </apply> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q1</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R1</id> </apply> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
関係は論理的に真です。

<region id="ID0EH6XMB" actualWidth="220.22000000000003" actualHeight="25.6" top="1401.6000000000001" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="22" xml:lang="ja">
 <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">M2</id>
 <apply xml:lang="ja">
 <id labels="FUNCTION" xml:space="preserve" xml:lang="ja" label-is-contextual="true">submatrix</id>
 <sequence xml:lang="ja">
 <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M1</id>
 <real xml:lang="ja">0</real>
 <real xml:lang="ja">1</real>
 <real xml:lang="ja">0</real>
 <real xml:lang="ja">2</real>
 </sequence>
 </apply>
 </define>
 <resultFormat xml:lang="ja">
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" />
 </resultFormat>
 </math>
</region>

<region id="ID0E4CYMB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1516.8000000000002" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="26" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">P2</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m2</id> <real xml:lang="ja">0</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EQDYMB" actualWidth="71.38666666666667" actualHeight="36.800000000000004" top="1516.8000000000002" left="134.40000000000003" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="28" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">Q2</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m2</id> <real xml:lang="ja">1</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EDEYMB" actualWidth="70.816666666666677" actualHeight="36.800000000000004" top="1516.8000000000002" left="230.40000000000003" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="30" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">R2</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m2</id> <real xml:lang="ja">2</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
<region id="ID0E1EYMB" actualWidth="153.23666666666668" actualHeight="25.6" top="1555.2000000000003" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="32" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <equal xml:lang="ja" /> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M2</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">P2</id> </apply> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q2</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R2</id> </apply> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
関係は論理的に真です。

<region id="ID0E6HYMB" actualWidth="220.22000000000003" actualHeight="25.6" top="1670.4000000000003" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="34" xml:lang="ja">
 <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">M3</id>
 <apply xml:lang="ja">
 <id labels="FUNCTION" xml:space="preserve" xml:lang="ja" label-is-contextual="true">submatrix</id>
 <sequence xml:lang="ja">
 <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M1</id>
 <real xml:lang="ja">0</real>
 <real xml:lang="ja">2</real>
 <real xml:lang="ja">0</real>
 <real xml:lang="ja">2</real>
 </sequence>
 </apply>
 </define>
 <resultFormat xml:lang="ja">
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" />
 </resultFormat>
 </math>
</region>

<region id="ID0EVLYMB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1785.6000000000004" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="38" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">P3</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m3</id> <real xml:lang="ja">0</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EIMYMB" actualWidth="71.38666666666667" actualHeight="36.800000000000004" top="1785.6000000000004" left="134.40000000000003" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="40" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">Q3</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m3</id> <real xml:lang="ja">1</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0E2MYMB" actualWidth="70.816666666666677" actualHeight="36.800000000000004" top="1785.6000000000004" left="230.40000000000003" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="42" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">R3</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m3</id> <real xml:lang="ja">2</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
<region id="ID0ESNYMB" actualWidth="153.23666666666668" actualHeight="25.6" top="1824.0000000000002" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="44" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <equal xml:lang="ja" /> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M3</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">P3</id> </apply> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q3</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R3</id> </apply> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
関係は論理的に真です。

<region id="ID0E4UYMB" actualWidth="140.69333333333333" actualHeight="81.4" top="2380.8" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="52" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M1</id> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EQVYMB" actualWidth="170.95" actualHeight="81.4" top="2380.8" left="211.20000000000005" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="54" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q10</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R10</id> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
<region id="ID0EHWYMB" actualWidth="142.05333333333334" actualHeight="25.6" top="2457.6000000000004" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="56" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <equal xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M1</id> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q10</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R10</id> </apply> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
関係は論理的に真です。

<region id="ID0EZ2YMB" actualWidth="87.346666666666664" actualHeight="36.800000000000004" top="2649.6000000000004" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="60" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">Q20</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m20</id> <real xml:lang="ja">0</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EM3YMB" actualWidth="86.776666666666671" actualHeight="36.800000000000004" top="2649.6000000000004" left="134.40000000000003" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="62" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">R20</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m20</id> <real xml:lang="ja">1</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
<region id="ID0ED4YMB" actualWidth="142.05333333333334" actualHeight="25.6" top="2688.0000000000005" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="64" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <equal xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M2</id> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q20</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R20</id> </apply> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
関係は論理的に真です。

<region id="ID0EUCZMB" actualWidth="87.346666666666664" actualHeight="36.800000000000004" top="2880.0000000000005" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="68" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">Q30</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m30</id> <real xml:lang="ja">0</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>	<region id="ID0EHDZMB" actualWidth="86.776666666666671" actualHeight="36.800000000000004" top="2880.0000000000005" left="134.40000000000003" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="70" xml:lang="ja"> <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja">R30</id> <apply xml:lang="ja"> <indexer xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">m30</id> <real xml:lang="ja">1</real> </apply> </define> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
<region id="ID0E5DZMB" actualWidth="142.05333333333334" actualHeight="25.6" top="2918.4000000000005" left="38.400000000000006" xml:lang="ja" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="72" xml:lang="ja"> <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50"> <apply xml:lang="ja"> <equal xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">M3</id> <apply xml:lang="ja"> <mult xml:lang="ja" /> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">Q30</id> <id labels="VARIABLE" xml:space="preserve" xml:lang="ja" label-is-contextual="true">R30</id> </apply> </apply> <unitOverride xml:lang="ja"> <placeholder xml:lang="ja" /> </unitOverride> </eval> <resultFormat xml:lang="ja"> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" xml:lang="ja" /> </resultFormat> </math> </region>
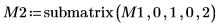
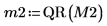
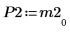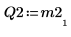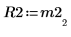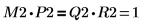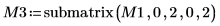
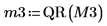
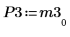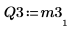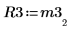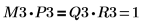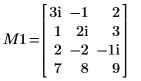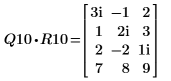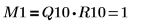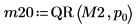
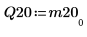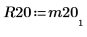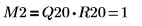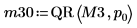
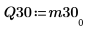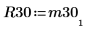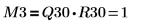関係は論理的に真です。