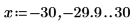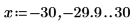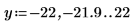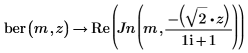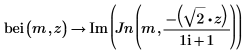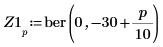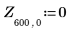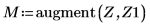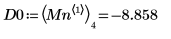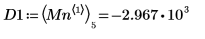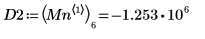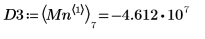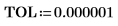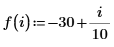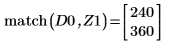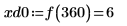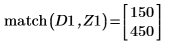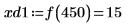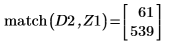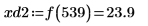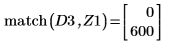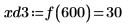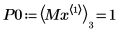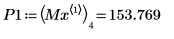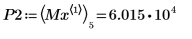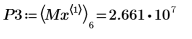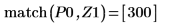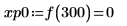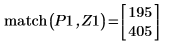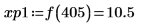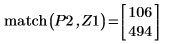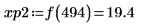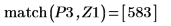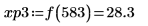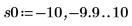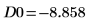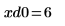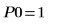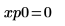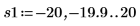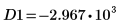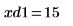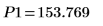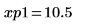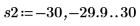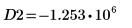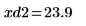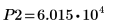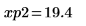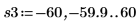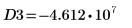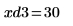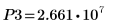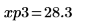例: ケルビン関数
関数
berおよび
beiの関係を示します。これらの関数には尺度化された型はありません。
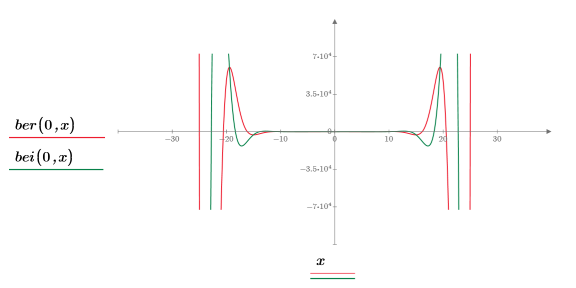
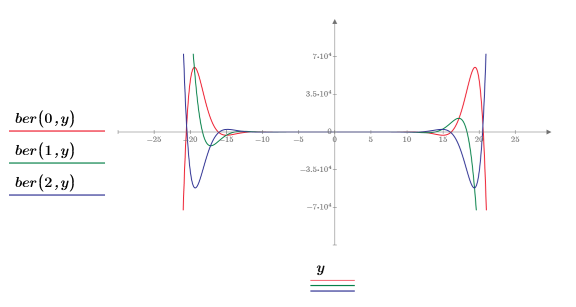
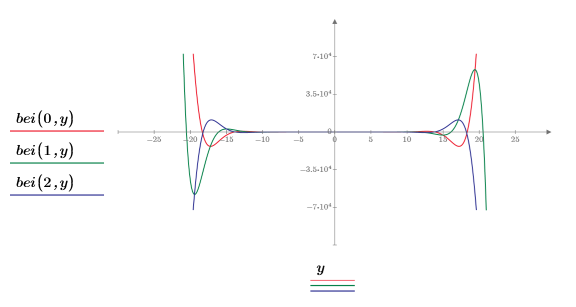
1. 0 次の関数 ber と bei を次のようにプロットします。
2 つの関数は対称に表示されます。
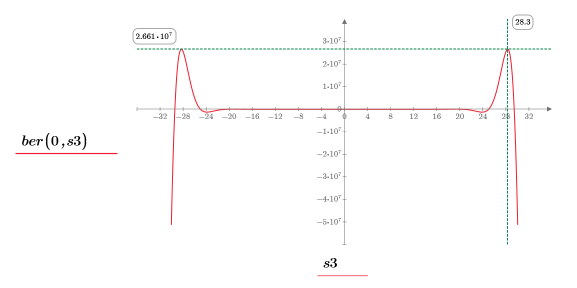
2. 目盛の値をリセットして X 軸を拡大し、次数を大きくした場合の関数 ber と bei の 2 つのピークの変化を表示します。
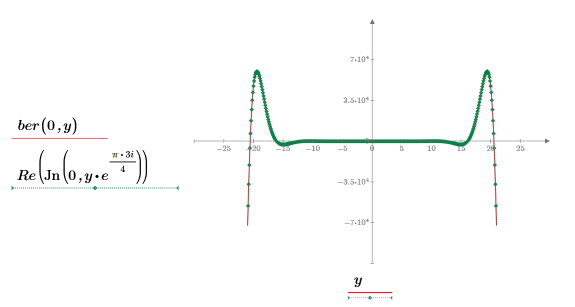
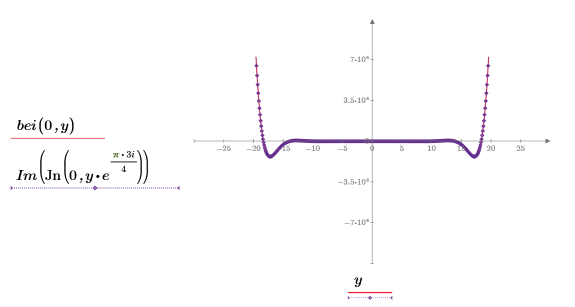
3. シンボリック評価を使用して
ber 関数と
bei 関数の
Jn関数との関係を示し、結果をプロットして視覚的に表示します。
この例では ber 関数に着目していますが、同じ測定値が関数 bei にも適用されます。
4. ベクトル Z1 を関数 ber を使用して次のように定義します。
5. 関数 ber の局所最小値を次のように求めます。
ber 関数には m=0 で 8 つの極小値があります。関数は対称です。高次関数にはさまざまな場所および振幅の、異なる数の極小値があります。
6. 関数 ber の局所最大値を次のように求めます。
ber 関数には m=0 で 7 つのピークがあります。関数は対称です。高次関数にはさまざまな場所および振幅の、異なる数の極大値があります。
7. 右側の 4 つの極小値の垂直座標を求めます。
8. 関数
matchを使用して、一致するそれぞれの極小値の添字を求めてから、これに等しい横方向の座標を求めます。
9. 右側の 4 つの極大値の垂直座標を求めます。
10. 関数 match を使用して、一致するそれぞれの極大値の添字を求めてから、これに等しい横方向の座標を求めます。
| 極大値と極小値の振幅の範囲は大幅に異なるので、1 つのプロットですべてを表示するのは困難です。 |
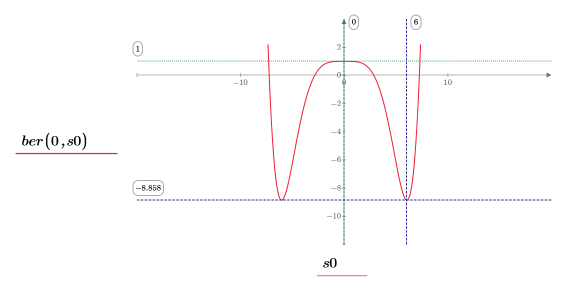
11. マーカーを使用して最初の極小値 (D0) と最初の極大値 (P0) を表示します。
予想どおり、グラフには 2 つ目の極小値が Y 軸の左に表示されます。
12. マーカーを使用して次の極小値 (D1) と次の極大値 (P1) を表示します。
予想どおり、グラフには 2 つ目の極小値と 2 つ目の極大値が Y 軸の左に表示されます。
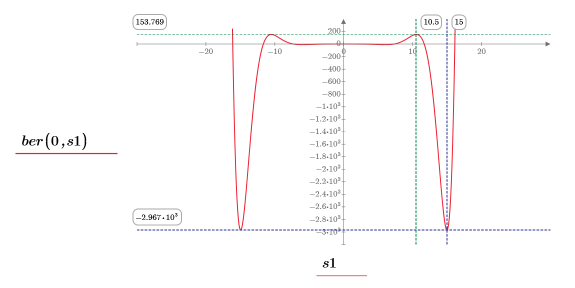
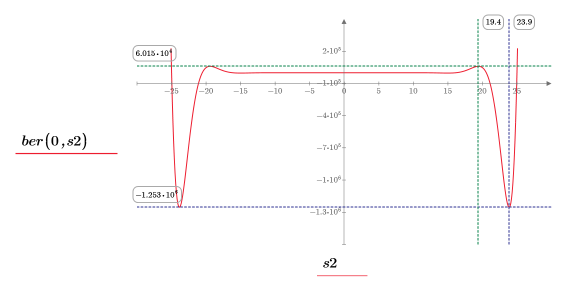
13. マーカーを使用して次の極小値 (D2) と次の極大値 (P2) を表示します。
予想どおり、グラフには 2 つ目の極小値と 2 つ目の極大値が Y 軸の左に表示されます。
14. マーカーを使用して次の極小値 (D3) と次の極大値 (P3) を表示します。
予想どおり、グラフには 2 つ目の極大値が Y 軸の左に表示されます。
| 極小値 (D3) とその左側の等価な極小値は厳密には範囲の端にあるので、これらは無視したほうが良いでしょう。 |