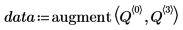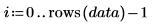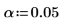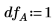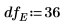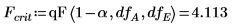例: ANOVA とブロック
block関数と
anova関数を使用して、計画行列を 2 つのブロックに分割し、ブロック化が結果に影響を与えるかどうかをテストします。
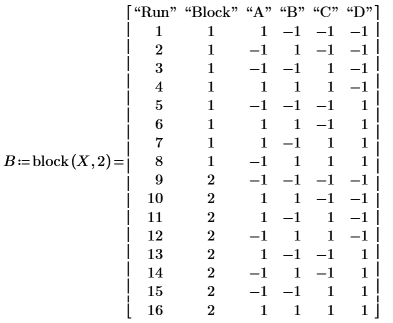
2. block 関数を呼び出して、計画行列 X を 2 つのブロックに分割します。
最初の 8 つのランが Block 1 に入り、残りのランが Block 2 に入ります。
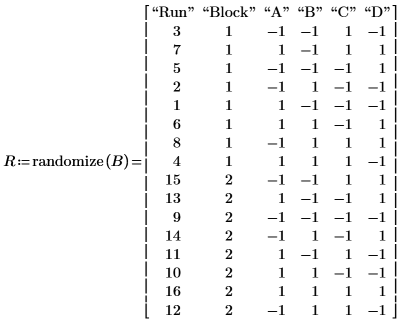
3. 実験を実行する前に
randomize関数を呼び出します。ブロックごとに無作為化が行われます。
4. 実験結果を行列 Y に格納します。行列の行によって、ブロック化された計画行列 B のどのランのデータであるかを識別し、列によってどのレプリケートのデータであるかを識別します。
7. 効果を 1/2 効果の絶対値に置き換えます。
8.
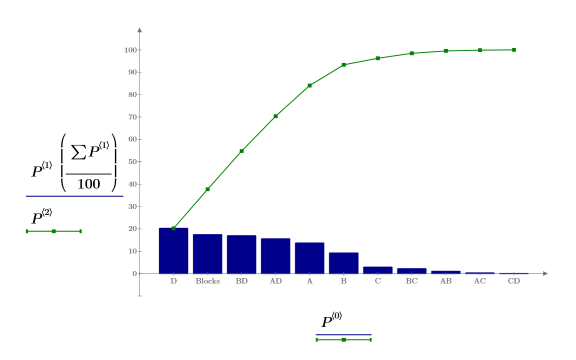
pareto関数を呼び出して、パレートグラフを作成します。
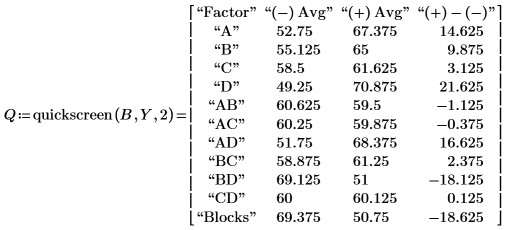
因子 A、B、D、交互作用 AD、BD、および Blocks は有意であると思われます。
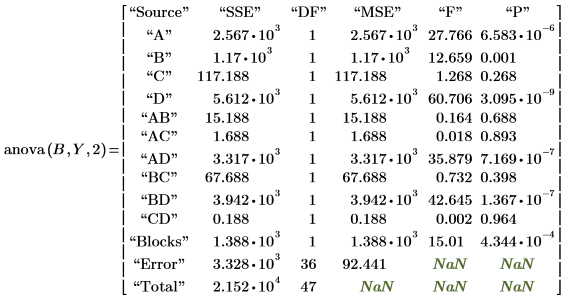
9. anova 関数を呼び出して分散分析を行います。因子、交互作用、およびブロック化の F-value の臨界値を計算します。F-value を F-value の臨界値と比較します。
10.
qF関数を使用して、因子、交互作用、およびブロック化の
F-value の臨界値を計算します。
F-value を
F-value の臨界値と比較します。
レベルを 5% に設定します。 | |
最低自由度 DF を設定します。 | |
最高自由度 DF を設定します。 | |
|
因子 A、B、D、交互作用 AD、BD、および Blocks は、それらの F 値が Fcrit を上回っているので、5% のレベルで有意です。この分散分析によって、パレートグラフから導かれた主観的な結論が裏付けされました。
参考文献
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 295.