多变量多项式回归
• polyfit(X, Y, n/"terms"/M) - 定义描述多变量多项式回归曲面的函数,该曲面将矩阵 Y 中所记录的结果拟合到矩阵 X 中找到的数据。您可按多项式阶数 n 或者在字符串 “terms” 或矩阵 M 中所指定的项来定义多项式回归方程。如果不想在多项式拟合中包括截距,请使用矩阵 M。
例如,请考虑多项式回归函数 p:
p := polyfit(X, Y ,1)
p(v) = 1.075
函数 p 取矢量自变量 v,按矩阵 X 的描述,指定 p 的每个自变量的值。矢量 v 中的每个变量必须具有与矩阵 X 的对应列兼容的单位。拟合函数 p 返回的单位与矩阵 Y 的单位兼容。
自变量
• X 为设计矩阵,或其中的每一列均代表一个自变量的矩阵。X 的每个列必须具有兼容单位。
• Y 为矢量,或者为测量结果或模拟结果的矩阵 (每一行都包含在 X 中定义的每个游程或数据点的结果)。当这些行并非都包含相同数量的副本时,您必须用 NaN 填充 Y 的空元素。矩阵 Y 的元素必须有兼容单位。
• n 是指定多项式阶数的整数。它必须小于数据点的总数:1 ≤ n ≤ length(Y) − 1。否则,问题欠约束,没有唯一解。
• “terms” 是字符串,用于指定要包括在多项式回归中的项 (或者因子和交互作用)。"A B AB AA BB" 表示多项式包含以下项:
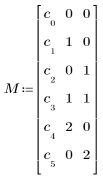
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
对于分隔符,您可以使用空格、逗号、冒号或分号。
• M 是矩阵,可用于为首列中的系数指定具有估值的多项式,以及为其余列中的各个项指定自变量的乘方。按照以下方法为上述多项式定义 M:
附加信息
regress 函数的输出是传递至 interp 函数以得到拟合函数的系数矩阵。
polyfit 函数的输出本身即是拟合函数,因此没有必要调用 interp 函数。