示例:拟合质量
使用 polyfit 和 polyfitstat 函数执行线性回归和方差分析,以测试拟合的质量。
1. 为聚合过程定义实验数据表。反应温度 t 和催化剂进料率 fr 会影响聚合的粘度 vy。

拟合功能性
2. 调用 polyfit 函数将数据建模为线性回归。
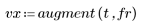
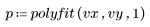
3. 计算为各个温度设置和进料率设置预测的粘度。
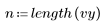
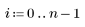
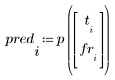
4. 计算残差 (计算的模型值与测量值之差)。
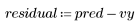
5. 绘制针对观察到的粘度、温度和进料率的残差。
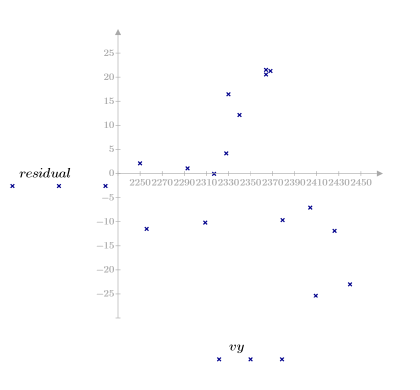
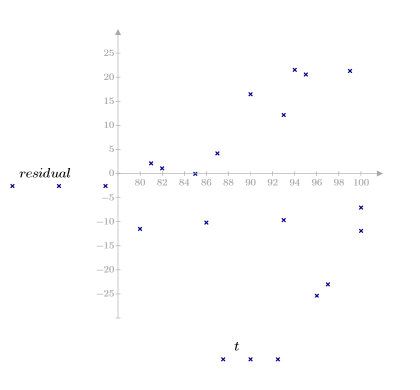
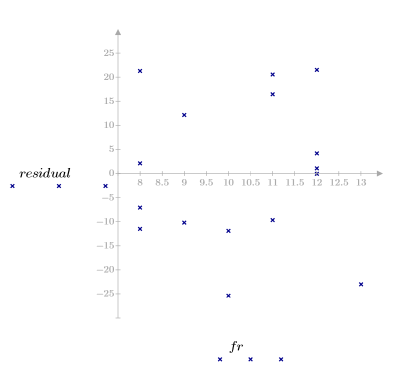
残差图指出,观察到的粘度和温度方差会分别随着粘度和温度量值的增大而增大。
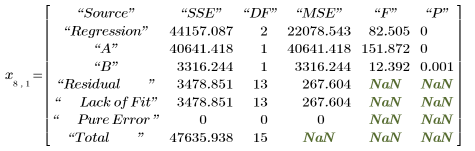
6. 调用 polyfitstat 函数计算线性模型的各种统计数据。在第 8 行显示由 polyfitstat 返回的 ANOVA 矩阵。
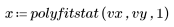
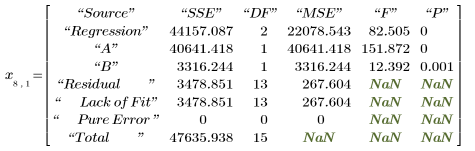
在 ANOVA 矩阵中,方差的源在 Regression (回归) 和 Residual (残差) 分量之间被分割。Regression (回归) 分量在各回归系数之间被进一步分割。但是,将无法针对残差来区分 Lack of Fit (失拟误差) 和 Pure Error (纯实验误差),因为实验结果 vy 没有副本。
针对回归计算以及使用 ANOVA 表
1. 计算由误差产生的平方和 (SSE)。
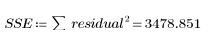
SSE 等于 χ2,是拟合度的一般度量。这是计算最小二乘解时达到的最小量。误差是模型与数据拟合度的量度。它显示了尚未被回归解释的偏差量。
2. 定义误差 df_error 相对于总自由度 df_total 的自由度以及参数 df_param 的自由度。自由度是扣除拟合参数个数的数据长度。
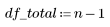
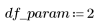
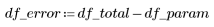
3. 相对于总平方和 (SST) 定义由回归产生的平方和 (SSR)。
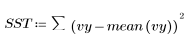
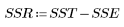
4. 定义均方误差 (MSE) 和均方回归 (MSR)。用相应的自由度除以误差。
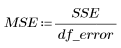
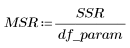
5. 形成方差表的分析以表征拟合。
平方和 | DF | 均方 | F 因子 | |
|---|---|---|---|---|
Regression | 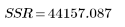 | 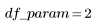 | 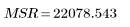 | 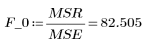 |
Error | 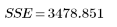 | 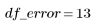 | 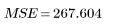 | |
Total | 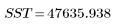 | 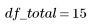 |
可以将上表和 polyfitstat ANOVA 矩阵加以比较。
6. 预估模型与数据的拟合度:
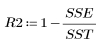
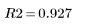
这说明线性回归模型解释了 92.7% 的粘度可变性。
7. 定义假设检验的显著性水平,以测试模型是否与数据拟合。
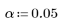
8. 计算临界的 F 值。
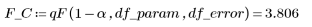
9. 对模型拟合数据的假设进行测试。
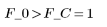
接受假设。可以使用此线性回归模型来预测聚合物的粘度。
参考文献
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 398