示例:了解压缩图像矩阵
通过 24 位二进制数 (其中,8 位为红色、8 位为绿色和 8 位为蓝色) 来表示单个 RGB 像素的值。可将这个 24 位二进制数视为 6 位十六进制数,其中包含两位最高有效数位、两位中间数位和两位最低有效数位,它们分别表示红色、绿色和蓝色的强度。黑色像素用十六进制值 0x000000 表示,而白色像素则用十六进制值 0xFFFFFF 来表示。中间的十六进制值可生成约 1680 万种可能颜色中的任何一种。
1. 定义矩阵缩放因子。
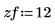
2. 定义零矩阵并使用 zoom 函数进行缩放。
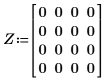
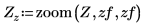
3. 定义三个完全相同的对应于压缩图像矩阵中 RGB 颜色分量的矩阵。

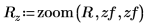

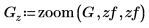

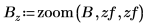
4. 使用 augment 函数创建压缩图像矩阵。
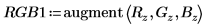
5. 使用 WRITERGB 函数将矩阵写入外部文件。
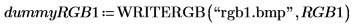
6. 在数学选项卡中,单击图像并浏览已写入的图像文件 rgb1.bmp,然后将其插入工作表。

该图像显示带有黑边的白色方块。白色是由压缩图像矩阵内三个分量强度 (R=255、G=255 和 B=255) 的组合效应所产生的结果。白色方块内的每个像素都具有十六进制值 0xFFFFFF。
7. 创建由 R、G/2 和 B/4 构成的新压缩图像矩阵。
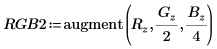
8. 将矩阵写入外部文件。
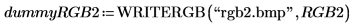
9. 单击图像,并浏览已写入的图像文件 rgb2.bmp,然后将其插入工作表。

该图像显示带有黑边的橙色方块。橙色是由压缩图像矩阵内三个分量强度 (R=255、G=128 和 B=64) 的组合效应所产生的结果。橙色方块内的每个像素都具有十六进制值 0xFF8040。
10. 创建由 R (但没有 G 或 B) 构成的新压缩图像矩阵。
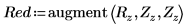
11. 将矩阵写入外部文件。
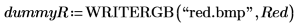
12. 单击图像,并浏览已写入的图像文件 red.bmp,然后将其插入工作表。

该图像显示带有黑边的红色方块。红色是由压缩图像矩阵内三个分量强度 (R=255、G=0 和 B=0) 的组合效应所产生的结果。红色方块内的每个像素都具有十六进制值 0xFF0000。
13. 创建由 G (但没有 R 和 B) 构成的新压缩图像矩阵。
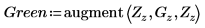
14. 将矩阵写入外部文件。
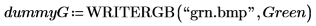
15. 单击图像,并浏览已写入的图像文件 grn.bmp,然后将其插入工作表。

该图像显示带有黑边的绿色方块。绿色是由压缩图像矩阵内三个分量强度 (R=0、G=255 和 B=0) 的组合效应所产生的结果。在绿色方块内的每个像素都具有十六进制值 0x00FF00。
16. 创建由 B (但没有 R 和 G) 构成的新压缩图像矩阵。
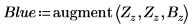
17. 将矩阵写入外部文件。
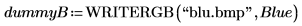
18. 单击图像,并浏览已写入的图像文件 blu.bmp,然后将其插入工作表。

该图像显示带有黑边的蓝色方块。蓝色是由压缩图像矩阵内三个分量强度 (R=0、G=0 和 B=255) 的组合效应所产生的结果。蓝色方块内的每个像素都具有十六进制值 0x0000FF。