示例:哈特利变换
使用函数 dht 求解信号的哈特利变换。
定义的哈特利变换之和类似于离散傅立叶变换之和。
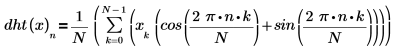
其中 N 为实数据数组 x 中元素的数目。
正弦波之和
求解正弦波之和的哈特利变换,并将其与复数形式傅立叶变换的幅度进行比较。
1. 定义元素的数目。
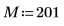
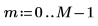
2. 使用函数 sin 定义输入信号。
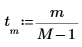
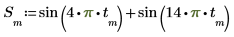
3. 绘制信号图像。
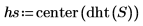
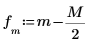
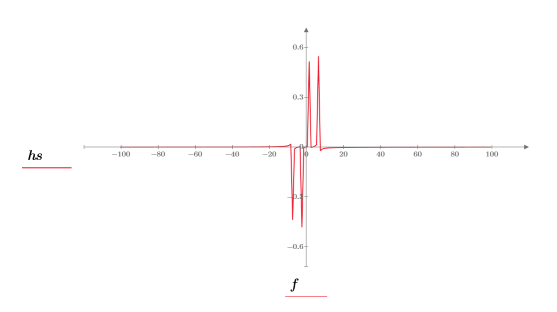
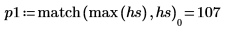
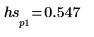
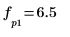
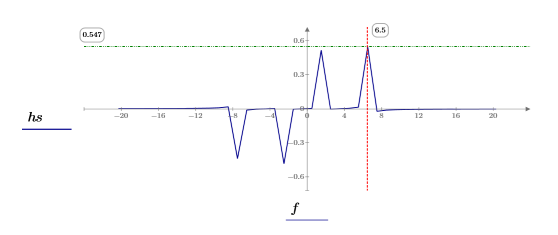
7. 绘制 DFT 的绝对值图像。
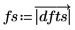
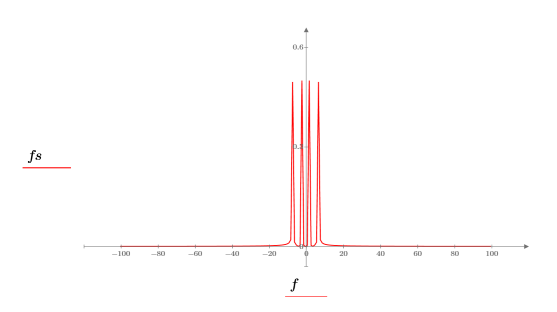
8. 使用函数 match 和 max 求峰值出现的离散频率。
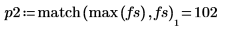
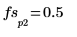
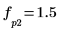
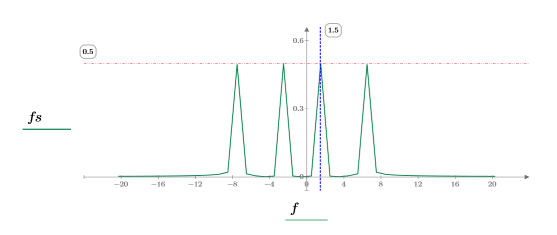
通过显示如何由哈特利变换计算相位和幅度,可证明哈特利变换与傅立叶变换之间的密切关系。这可使用小数据集来完成。
短信号和噪声信号
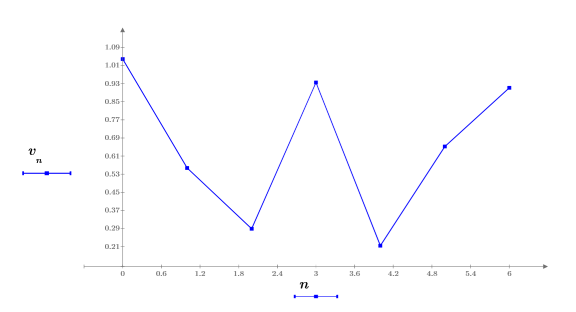
1. 定义 7 个样本点的有噪输入信号并绘制其图像。
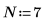
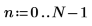
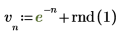
2. 计算离散哈特利变换并使其居中。
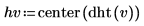
3. 计算哈特利变换的奇部和偶部 (这些公式假定奇数值 N)。
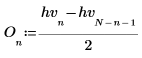 | 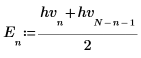 |
4. 使用函数 angle 计算相位矢量。
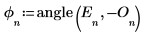
5. 定义幅度矢量。
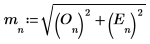
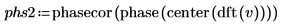
7. 使用函数 augment 比较相位结果以及通过傅立叶变换得到的结果。

相位结果一致。
8. 使用函数 dft 和 center 创建幅度矢量。
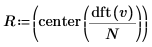
9. 使用函数 augment 比较幅度结果以及通过傅立叶变换得到的结果。
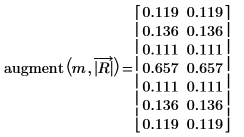
幅度结果一致。
有关哈特利变换的详细介绍及其应用,请参阅 Oxford University Press 出版的 Ronald Bracewell 所著的《The Hartley Transform》(《哈特利变换》)。