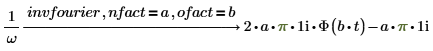示例:符号变换
执行符号形式的傅立叶、拉普拉斯和以及 Z 变换及其逆变换。
傅立叶变换以及傅立叶逆变换
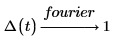
正如所预期的那样,该运算返回恒定频率。
2. 求涉及海维赛德阶梯函数 Φ 的函数的傅立叶变换。
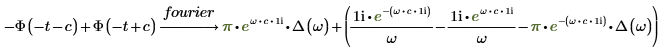
3. 添加 simplify 关键字来简化结果。
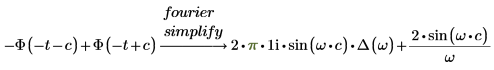
Z 变换和逆 Z 变换
1. 使用关键字 ztrans 来计算以下两个函数的 z 变换:
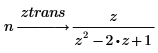
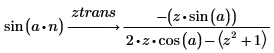
2. 使用关键字 invztrans 来计算以下两个函数的逆 z 变换:
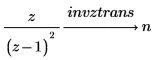
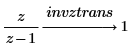
更改变换的默认变量
1. 求函数的拉普拉斯逆变换。
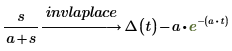
2. 通过在变换关键字后添加一对自变量,更改由拉普拉斯逆变换返回的函数中的默认变量 t。
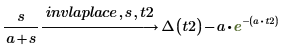
◦ 第一个自变量 s 是域函数的独立变量。
◦ 第二个自变量 t2 是已变换函数的新独立变量。
◦ 返回的拉普拉斯逆变换使用变量 t2 作为独立变量。Δ 是 Dirac Delta 函数。
◦ 尽管不能使用数值等号计算 Δ,但可使用符号求值运算符进行计算。
3. 使用关键字 laplace 求结果的拉普拉斯变换。
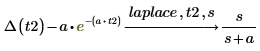
一次使用多个关键字
如果符号计算结果并非您所需要的形式,可在变换关键字后添加一个关键字来修改结果的格式。
1. 求函数的 z 变换。
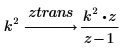
2. 使用关键字 expand 来展开结果。
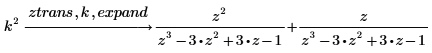
3. 使用关键字 laplace 来求函数的拉普拉斯变换。
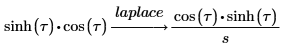
4. 使用关键字 simplify 获取简化结果。
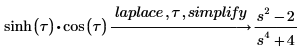
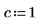
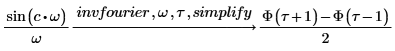
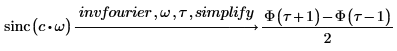
对于没有符号变换的输入函数,可使用数值 dft 函数。
傅立叶变换因式分解
1. 向表达式中添加 nfact ofact 和 fourier。
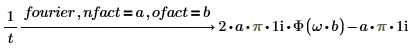
2. 向表达式中添加 nfact ofact 和 invfourier。