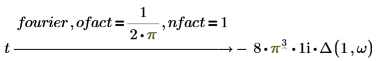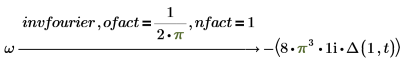示例：使用 nfact 和 ofact 修饰符

符号 > 关键字和修饰符 > 示例：使用 nfact 和 ofact 修饰符

归一化乘数 (nfact) 和振荡因子 (ofact) 的表达式如下：

<region id="ID0ESFXLB" actualWidth="378.38166666666666" actualHeight="58.952000000000005" top="76.800000000000011" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="60">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <id xml:space="preserve">a</id>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <id xml:space="preserve">b</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <mult />
          <id xml:space="preserve" labels="VARIABLE">a</id>
          <apply>
            <integral />
            <lambda>
              <boundVars>
                <id xml:space="preserve" labels="VARIABLE">t</id>
              </boundVars>
              <apply>
                <mult />
                <apply>
                  <id xml:space="preserve" labels="VARIABLE">f</id>
                  <id xml:space="preserve" labels="VARIABLE">t</id>
                </apply>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="CONSTANT">e</id>
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">ω</id>
                        <id xml:space="preserve" labels="VARIABLE">b</id>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <imag symbol="i">1</imag>
                  </apply>
                </apply>
              </apply>
            </lambda>
            <lowerBound>
              <apply>
                <neg />
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </apply>
            </lowerBound>
            <upperBound>
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </upperBound>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EBGXLB" actualWidth="414.68166666666667" actualHeight="58.952000000000005" top="153.60000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="61">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <id xml:space="preserve">a</id>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <id xml:space="preserve">b</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <mult />
          <id xml:space="preserve" labels="VARIABLE">a</id>
          <apply>
            <integral />
            <lambda>
              <boundVars>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </boundVars>
              <apply>
                <mult />
                <apply>
                  <id xml:space="preserve" labels="VARIABLE">f</id>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </apply>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="CONSTANT">e</id>
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">ω</id>
                        <id xml:space="preserve" labels="VARIABLE">b</id>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <imag symbol="i">1</imag>
                  </apply>
                </apply>
              </apply>
            </lambda>
            <lowerBound>
              <apply>
                <neg />
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </apply>
            </lowerBound>
            <upperBound>
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </upperBound>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

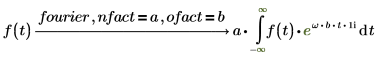
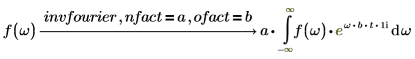
傅立叶变换和逆傅立叶变换仅归一化和振荡因子不同。这两种因子的选择通常是为了后续的直接变换和逆变换能够得出原函数。例如：

<region id="ID0EVGXLB" actualWidth="379.78999999999996" actualHeight="51.158666666666669" top="307.20000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <symEval>
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Φ</id>
          <id xml:space="preserve">t</id>
        </apply>
        <command>
          <id xml:space="preserve">fourier</id>
        </command>
        <symResult>
          <apply>
            <plus />
            <apply>
              <mult />
              <id xml:space="preserve" labels="CONSTANT">π</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">Δ</id>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </apply>
            </apply>
            <apply>
              <div />
              <imag symbol="i">1</imag>
              <id xml:space="preserve" labels="VARIABLE">ω</id>
            </apply>
          </apply>
        </symResult>
      </symEval>
      <command>
        <sequence>
          <id xml:space="preserve">invfourier</id>
          <id xml:space="preserve">simplify</id>
        </sequence>
      </command>
      <symResult>
        <apply>
          <id xml:space="preserve" labels="FUNCTION">Φ</id>
          <id xml:space="preserve" labels="VARIABLE">t</id>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

<region id="ID0EEHXLB" actualWidth="686.95000000000016" actualHeight="72.75866666666667" top="384.00000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="63">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <symEval>
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Φ</id>
          <id xml:space="preserve">t</id>
        </apply>
        <command>
          <sequence>
            <sequence>
              <id xml:space="preserve">fourier</id>
              <apply>
                <equal />
                <id xml:space="preserve">nfact</id>
                <real>1</real>
              </apply>
            </sequence>
            <apply>
              <equal />
              <id xml:space="preserve">ofact</id>
              <real>1</real>
            </apply>
          </sequence>
        </command>
        <symResult>
          <apply>
            <plus />
            <apply>
              <mult />
              <id xml:space="preserve" labels="CONSTANT">π</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">Δ</id>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </apply>
            </apply>
            <apply>
              <div />
              <imag symbol="i">1</imag>
              <id xml:space="preserve" labels="VARIABLE">ω</id>
            </apply>
          </apply>
        </symResult>
      </symEval>
      <command>
        <sequence>
          <sequence>
            <sequence>
              <id xml:space="preserve">invfourier</id>
              <apply>
                <equal />
                <id xml:space="preserve">nfact</id>
                <apply>
                  <div />
                  <real>1</real>
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                  </apply>
                </apply>
              </apply>
            </sequence>
            <apply>
              <equal />
              <id xml:space="preserve">ofact</id>
              <real>-1</real>
            </apply>
          </sequence>
          <id xml:space="preserve">simplify</id>
        </sequence>
      </command>
      <symResult>
        <apply>
          <id xml:space="preserve" labels="FUNCTION">Φ</id>
          <id xml:space="preserve" labels="VARIABLE">t</id>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

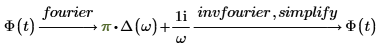
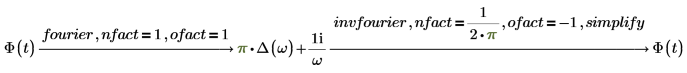
在不同的数学和工程字段中选择不同的归一化和振荡因子对以将不同类型的信号进行归一化。

1. 概率论 (无单位模型)

<region id="ID0ELJXLB" actualWidth="250.61333333333334" actualHeight="39.2" top="614.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="65">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <real>1</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EHKXLB" actualWidth="336.79666666666674" actualHeight="72.75866666666667" top="748.80000000000007" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="67">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <real>1</real>
          <apply>
            <mult />
            <real>2</real>
            <id xml:space="preserve" labels="CONSTANT">π</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EVKXLB" actualWidth="213.92166666666668" actualHeight="58.952000000000005" top="806.40000000000009" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="68">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <id xml:space="preserve">fourier</id>
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id xml:space="preserve" labels="VARIABLE">t</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <id xml:space="preserve" labels="VARIABLE">f</id>
                <id xml:space="preserve" labels="VARIABLE">t</id>
              </apply>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">ω</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <imag symbol="i">1</imag>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <apply>
              <neg />
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </apply>
          </lowerBound>
          <upperBound>
            <id xml:space="preserve" labels="CONSTANT">∞</id>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EDLXLB" actualWidth="269.66500000000008" actualHeight="80.552" top="902.40000000000009" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="69">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <id xml:space="preserve">invfourier</id>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <integral />
            <lambda>
              <boundVars>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </boundVars>
              <apply>
                <mult />
                <apply>
                  <id xml:space="preserve" labels="VARIABLE">f</id>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </apply>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="CONSTANT">e</id>
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">ω</id>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <imag symbol="i">1</imag>
                      </apply>
                    </parens>
                  </apply>
                </apply>
              </apply>
            </lambda>
            <lowerBound>
              <apply>
                <neg />
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </apply>
            </lowerBound>
            <upperBound>
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </upperBound>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <id xml:space="preserve" labels="CONSTANT">π</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ERLXLB" actualWidth="350.0483333333334" actualHeight="58.952000000000005" top="960.00000000000011" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="70">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id xml:space="preserve" labels="VARIABLE">t</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <id xml:space="preserve" labels="VARIABLE">f</id>
                <id xml:space="preserve" labels="VARIABLE">t</id>
              </apply>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">ω</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <imag symbol="i">1</imag>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <apply>
              <neg />
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </apply>
          </lowerBound>
          <upperBound>
            <id xml:space="preserve" labels="CONSTANT">∞</id>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E6LXLB" actualWidth="440.69833333333344" actualHeight="80.552" top="1036.8000000000002" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="71">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <integral />
            <lambda>
              <boundVars>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </boundVars>
              <apply>
                <mult />
                <apply>
                  <id xml:space="preserve" labels="VARIABLE">f</id>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </apply>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="CONSTANT">e</id>
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">ω</id>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <imag symbol="i">1</imag>
                      </apply>
                    </parens>
                  </apply>
                </apply>
              </apply>
            </lambda>
            <lowerBound>
              <apply>
                <neg />
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </apply>
            </lowerBound>
            <upperBound>
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </upperBound>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <id xml:space="preserve" labels="CONSTANT">π</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

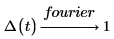
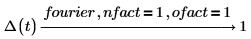
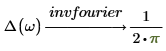
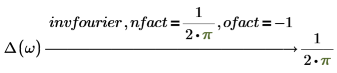
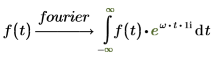
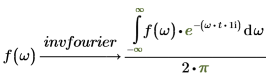
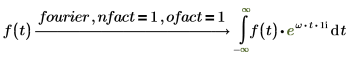
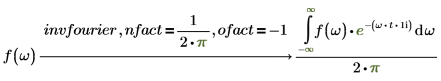
2. 电气工程 (频率单位为赫兹，Wolfram 集之一)

<region id="ID0EPNXLB" actualWidth="280.72" actualHeight="39.2" top="1152.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="72">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <apply>
              <mult />
              <real>-2</real>
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
            </apply>
          </apply>
        </sequence>
      </command>
      <symResult>
        <real>1</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E4NXLB" actualWidth="297.09000000000003" actualHeight="39.2" top="1209.6000000000001" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="73">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <apply>
              <mult />
              <real>2</real>
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
            </apply>
          </apply>
        </sequence>
      </command>
      <symResult>
        <real>1</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ELOXLB" actualWidth="420.75166666666667" actualHeight="58.952000000000005" top="1267.2000000000003" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="74">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <apply>
              <mult />
              <real>-2</real>
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
            </apply>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id xml:space="preserve" labels="VARIABLE">t</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <id xml:space="preserve" labels="VARIABLE">f</id>
                <id xml:space="preserve" labels="VARIABLE">t</id>
              </apply>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <neg />
                  <parens>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <apply>
                            <mult />
                            <real>2</real>
                            <id xml:space="preserve" labels="VARIABLE">ω</id>
                          </apply>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <id xml:space="preserve" labels="CONSTANT">π</id>
                      </apply>
                      <imag symbol="i">1</imag>
                    </apply>
                  </parens>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <apply>
              <neg />
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </apply>
          </lowerBound>
          <upperBound>
            <id xml:space="preserve" labels="CONSTANT">∞</id>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EZOXLB" actualWidth="431.65833333333342" actualHeight="58.952000000000005" top="1324.8000000000002" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="75">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <apply>
              <mult />
              <real>2</real>
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
            </apply>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id xml:space="preserve" labels="VARIABLE">ω</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <id xml:space="preserve" labels="VARIABLE">f</id>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </apply>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">ω</id>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <id xml:space="preserve" labels="CONSTANT">π</id>
                  </apply>
                  <imag symbol="i">1</imag>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <apply>
              <neg />
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </apply>
          </lowerBound>
          <upperBound>
            <id xml:space="preserve" labels="CONSTANT">∞</id>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

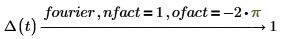
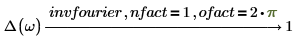
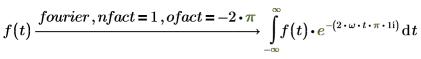
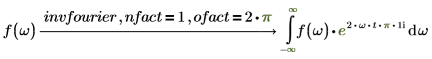
3. 电气工程 (采用角频率)

<region id="ID0EJQXLB" actualWidth="261.36333333333334" actualHeight="39.2" top="1440.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="76">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <real>1</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EXQXLB" actualWidth="326.04666666666674" actualHeight="72.75866666666667" top="1516.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="77">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <real>1</real>
          <apply>
            <mult />
            <real>2</real>
            <id xml:space="preserve" labels="CONSTANT">π</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EFRXLB" actualWidth="375.44166666666672" actualHeight="58.952000000000005" top="1574.4000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="78">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id xml:space="preserve" labels="VARIABLE">t</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <id xml:space="preserve" labels="VARIABLE">f</id>
                <id xml:space="preserve" labels="VARIABLE">t</id>
              </apply>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <neg />
                  <parens>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">ω</id>
                        <id xml:space="preserve" labels="VARIABLE">t</id>
                      </apply>
                      <imag symbol="i">1</imag>
                    </apply>
                  </parens>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <apply>
              <neg />
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </apply>
          </lowerBound>
          <upperBound>
            <id xml:space="preserve" labels="CONSTANT">∞</id>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ETRXLB" actualWidth="415.30500000000006" actualHeight="80.552" top="1651.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="79">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <integral />
            <lambda>
              <boundVars>
                <id xml:space="preserve" labels="VARIABLE">ω</id>
              </boundVars>
              <apply>
                <mult />
                <apply>
                  <id xml:space="preserve" labels="VARIABLE">f</id>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </apply>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="CONSTANT">e</id>
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">ω</id>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <imag symbol="i">1</imag>
                  </apply>
                </apply>
              </apply>
            </lambda>
            <lowerBound>
              <apply>
                <neg />
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </apply>
            </lowerBound>
            <upperBound>
              <id xml:space="preserve" labels="CONSTANT">∞</id>
            </upperBound>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <id xml:space="preserve" labels="CONSTANT">π</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

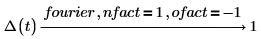
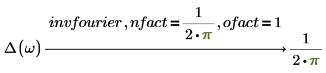
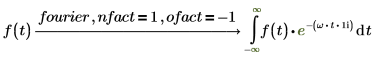
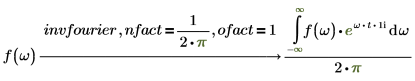
4. 变换在直接对称和逆对称中至关重要。相同的输入 (具有不同的变换变量) 可通过使用适当的 nfact 和 ofact 值集返回相同的输出结果。

<region id="ID0ELTXLB" actualWidth="339.49533395926159" actualHeight="85.249333721319843" top="1785.6000000000004" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="80">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                  </apply>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <nthRoot />
            <placeholder />
            <real>2</real>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <apply>
              <nthRoot />
              <placeholder />
              <id xml:space="preserve" labels="CONSTANT">π</id>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EZTXLB" actualWidth="355.86533395926165" actualHeight="85.249333721319843" top="1900.8000000000002" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="81">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Δ</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                  </apply>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <nthRoot />
            <placeholder />
            <real>2</real>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <apply>
              <nthRoot />
              <placeholder />
              <id xml:space="preserve" labels="CONSTANT">π</id>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EHUXLB" actualWidth="451.08033395926157" actualHeight="86.7973335273266" top="2016.0000000000002" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="82">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">t</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                  </apply>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <mult />
            <apply>
              <nthRoot />
              <placeholder />
              <real>2</real>
            </apply>
            <apply>
              <integral />
              <lambda>
                <boundVars>
                  <id xml:space="preserve" labels="VARIABLE">t</id>
                </boundVars>
                <apply>
                  <mult />
                  <apply>
                    <id xml:space="preserve" labels="VARIABLE">f</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="CONSTANT">e</id>
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <apply>
                            <mult />
                            <id xml:space="preserve" labels="VARIABLE">ω</id>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                          <imag symbol="i">1</imag>
                        </apply>
                      </parens>
                    </apply>
                  </apply>
                </apply>
              </lambda>
              <lowerBound>
                <apply>
                  <neg />
                  <id xml:space="preserve" labels="CONSTANT">∞</id>
                </apply>
              </lowerBound>
              <upperBound>
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </upperBound>
            </apply>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <apply>
              <nthRoot />
              <placeholder />
              <id xml:space="preserve" labels="CONSTANT">π</id>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EVUXLB" actualWidth="461.98700062592832" actualHeight="86.7973335273266" top="2112.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="83">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">f</id>
        <id xml:space="preserve">ω</id>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">nfact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                  </apply>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <mult />
            <apply>
              <nthRoot />
              <placeholder />
              <real>2</real>
            </apply>
            <apply>
              <integral />
              <lambda>
                <boundVars>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </boundVars>
                <apply>
                  <mult />
                  <apply>
                    <id xml:space="preserve" labels="VARIABLE">f</id>
                    <id xml:space="preserve" labels="VARIABLE">ω</id>
                  </apply>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="CONSTANT">e</id>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">ω</id>
                        <id xml:space="preserve" labels="VARIABLE">t</id>
                      </apply>
                      <imag symbol="i">1</imag>
                    </apply>
                  </apply>
                </apply>
              </lambda>
              <lowerBound>
                <apply>
                  <neg />
                  <id xml:space="preserve" labels="CONSTANT">∞</id>
                </apply>
              </lowerBound>
              <upperBound>
                <id xml:space="preserve" labels="CONSTANT">∞</id>
              </upperBound>
            </apply>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <apply>
              <nthRoot />
              <placeholder />
              <id xml:space="preserve" labels="CONSTANT">π</id>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

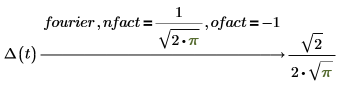
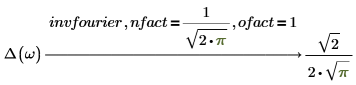
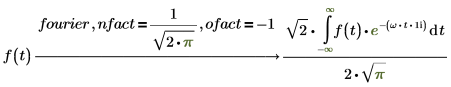
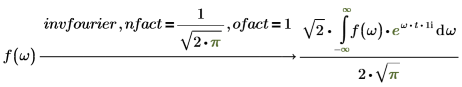
傅立叶和逆傅立叶之间的可逆性

若对输入表达式应用关键字 fourier，则对结果应用关键字 invfourier 必将返回初始表达式。当关键字 fourier 或 invfourier 与默认修饰符 nfact 和 ofact 搭配使用时具有可逆性。

在使用修饰符 nfact 和 ofact 时，以下条件适用：

• 关键字名称后紧跟修饰符 nfact 和 ofact。可分别使用这两个修饰符或将二者纳入同一表达式。

<region id="ID0EQYXLB" actualWidth="270.72333333333336" actualHeight="60.800000000000004" top="2284.8" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="84">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve">t</id>
      <command>
        <sequence>
          <id xml:space="preserve">fourier</id>
          <apply>
            <equal />
            <id xml:space="preserve">nfact</id>
            <apply>
              <div />
              <real>1</real>
              <apply>
                <mult />
                <real>2</real>
                <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
              </apply>
            </apply>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <neg />
          <parens>
            <apply>
              <mult />
              <imag symbol="i">1</imag>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">Δ</id>
                <sequence>
                  <real>1</real>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </sequence>
              </apply>
            </apply>
          </parens>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E5YXLB" actualWidth="268.98666666666668" actualHeight="39.2" top="2342.4000000000005" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="85">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve">t</id>
      <command>
        <sequence>
          <id xml:space="preserve">fourier</id>
          <apply>
            <equal />
            <id xml:space="preserve">ofact</id>
            <real>-1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <mult />
          <apply>
            <mult />
            <apply>
              <mult />
              <real>2</real>
              <id xml:space="preserve" labels="CONSTANT">π</id>
            </apply>
            <imag symbol="i">1</imag>
          </apply>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">Δ</id>
            <sequence>
              <real>1</real>
              <id xml:space="preserve" labels="VARIABLE">ω</id>
            </sequence>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

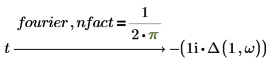
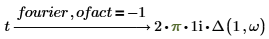
• 不得将矩阵用作因子。

<region id="ID0EO1XLB" actualWidth="224.26666666666668" actualHeight="60.800000000000004" top="2457.6000000000004" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="86">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve">t</id>
      <command>
        <sequence>
          <sequence>
            <sequence>
              <id xml:space="preserve">fourier</id>
              <apply>
                <equal />
                <id xml:space="preserve">nfact</id>
                <matrix rows="1" cols="1">
                  <apply>
                    <div />
                    <real>1</real>
                    <apply>
                      <mult />
                      <real>2</real>
                      <id xml:space="preserve">π</id>
                    </apply>
                  </apply>
                </matrix>
              </apply>
            </sequence>
            <id xml:space="preserve">t</id>
          </sequence>
          <id xml:space="preserve">s</id>
        </sequence>
      </command>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E31XLB" actualWidth="246.79666666666668" actualHeight="60.800000000000004" top="2534.4000000000005" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="87">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve">t</id>
      <command>
        <sequence>
          <sequence>
            <sequence>
              <id xml:space="preserve">invfourier</id>
              <apply>
                <equal />
                <id xml:space="preserve">nfact</id>
                <matrix rows="1" cols="1">
                  <apply>
                    <div />
                    <real>1</real>
                    <apply>
                      <mult />
                      <real>2</real>
                      <id xml:space="preserve">π</id>
                    </apply>
                  </apply>
                </matrix>
              </apply>
            </sequence>
            <id xml:space="preserve">t</id>
          </sequence>
          <id xml:space="preserve">s</id>
        </sequence>
      </command>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

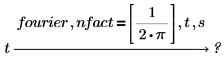
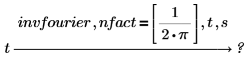
• 这两个修饰符支持逆傅立叶变换。

<region id="ID0EM3XLB" actualWidth="382.86333333333334" actualHeight="60.800000000000004" top="2649.6000000000004" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="88">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve">t</id>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">ofact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">nfact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <neg />
          <parens>
            <apply>
              <mult />
              <apply>
                <mult />
                <apply>
                  <mult />
                  <real>8</real>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="CONSTANT">π</id>
                    <real>3</real>
                  </apply>
                </apply>
                <imag symbol="i">1</imag>
              </apply>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">Δ</id>
                <sequence>
                  <real>1</real>
                  <id xml:space="preserve" labels="VARIABLE">ω</id>
                </sequence>
              </apply>
            </apply>
          </parens>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E13XLB" actualWidth="405.39333333333337" actualHeight="60.800000000000004" top="2726.4000000000005" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="89">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve">ω</id>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">invfourier</id>
            <apply>
              <equal />
              <id xml:space="preserve">ofact</id>
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">π</id>
                </apply>
              </apply>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">nfact</id>
            <real>1</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <neg />
          <parens>
            <apply>
              <mult />
              <apply>
                <mult />
                <apply>
                  <mult />
                  <real>8</real>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="CONSTANT">π</id>
                    <real>3</real>
                  </apply>
                </apply>
                <imag symbol="i">1</imag>
              </apply>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">Δ</id>
                <sequence>
                  <real>1</real>
                  <id xml:space="preserve" labels="VARIABLE">t</id>
                </sequence>
              </apply>
            </apply>
          </parens>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

这对您有帮助吗?