示例:噪声生成器
白噪声
whiten 函数可模拟由 N 个独立源产生的噪声,其中每个声源均具有在 -0.5 和 0.5 之间均匀分布的随机输出。
1. 使用 whiten 函数计算六个独立噪声源的白噪声函数。

对 whiten 函数进行的重复计算得出另一组矢量元素。
2. 考虑略大的输出矢量。
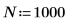
3. 绘制白噪声函数的图像。
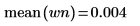
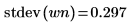
5. 显示理论平均值,然后使用 var 函数计算标准差。
绘图中显示,wn 信号的理论平均值为 0。 | |
标准差是方差的平方根。 | 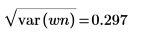 |
6. 将计算所得的平均值和标准差值与其理论值进行比较,并确认这些值彼此之间没有明显偏离。
高斯噪声
gaussn 函数模拟 x 个独立源,其中每个独立源均遵照平均值为 0、标准差为 1 的高斯概率分布。
1. 计算六个独立噪声源的 gaussian 噪声函数。

理论上,矢量的元素可以为任何实数值,但最有可能在 -3 到 +3 之间。您可以通过按 F5 键重新计算函数对此进行验证。
2. 绘制样本高斯序列图像。
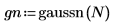
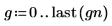
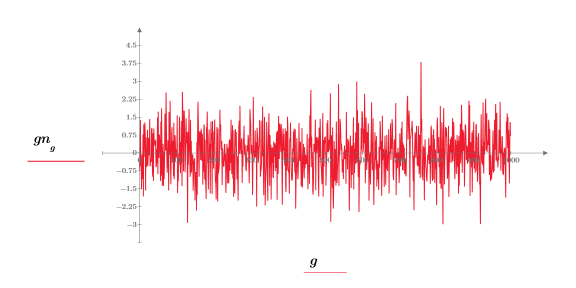
3. 准备钟形柱状图的高斯数据 (将值划分至 20 个宽度为 0.05 的柱)。
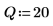
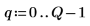
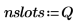
4. 定义包含柱边界的矢量,然后设置最右侧的边界。
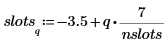
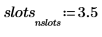
5. 使用 hist 函数来创建柱状图,然后将其绘制为条形图。
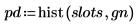
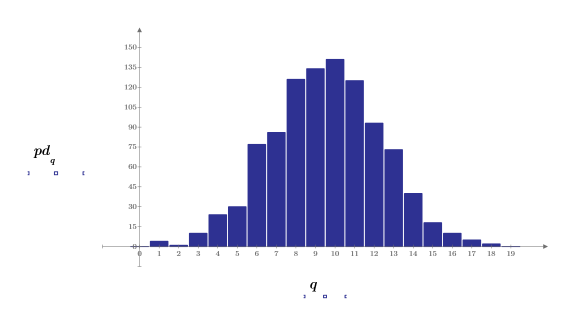
6. 将样本的平均值和标准差与预期值 0 和 1 进行比较。
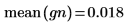
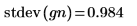
1/f 噪声
onefn 函数使用基于由 Richard Voss 所开发的算法 (请参阅 Scientific American 1978 年 4 月出版的 Martin Gardner's column) 的程序来计算 1/f 噪声的近似值。
1. 使用 onefn 函数生成由 1000 个点构成的矢量 1/f。
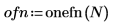
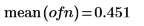
2. 调整为平均值 0。
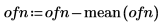
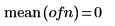
3. 绘制矢量数据的图像。
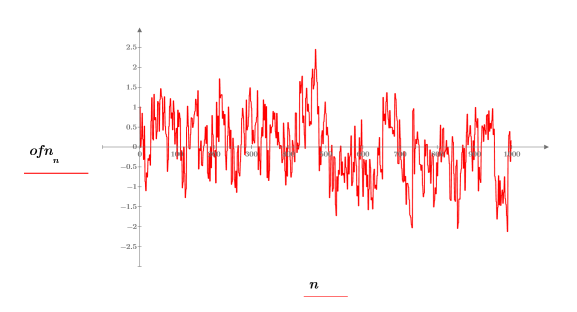
可在多种自然与人为现象 (包括音乐、脑信号、天气、股票市场动态以及其他分级交互体系) 的信号中找出 1/f 噪声。例如,如果要对各种风格 (摇滚乐、爵士乐、古典乐) 音乐的样本进行数字化处理,则会发现其功率谱的 1/f 噪声分布非常接近。
4. 使用 lcorr 函数将此噪声的统计结构与通过计算其自相关而生成的上述白噪声进行比较。
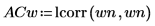
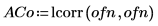
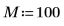
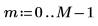
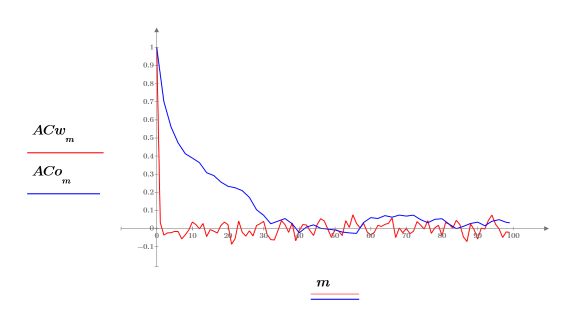
与白噪声不同,由 onefn 生成的噪声是相关的,相关性随着延迟的增加而衰减。
使用功率谱比较噪声信号
查看白噪声和 1/f 噪声之间差异的另一种方法是比较它们的功率谱。
1. 假设将频率的 50 个柱分成 20 个组。
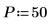
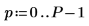
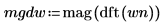
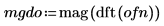
3. 通过对所有频率组进行平均化来平滑结果。
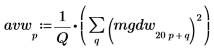
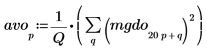
4. 绘制白噪声谱的图像。
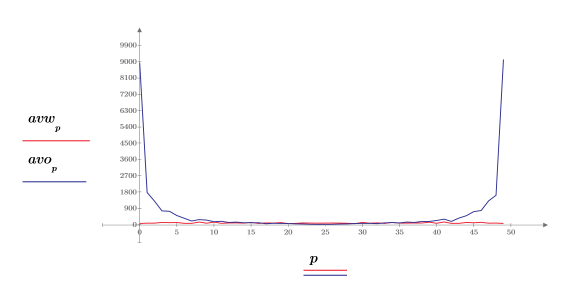
正如所预期的那样,白噪声谱基本上是平的。随着频率的增加 1/f 近似值的幅度频谱迅速下降。
5. 使用 log 函数来计算更有意义的幅度对数。
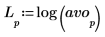
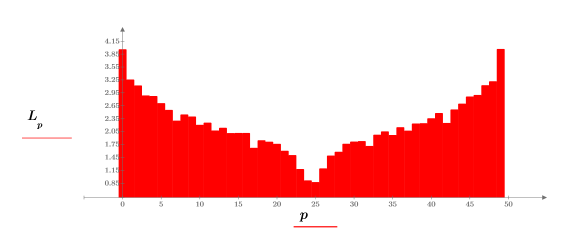
实验
作为实验,尝试使用随机相位构建 1/f 功率谱,并进行逆变换来获取噪声矢量。
1. 定义频谱宽度。
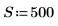
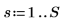
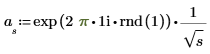
3. 计算变换的后半部分 (对于实数信号,后半部分绕中点成共轭对称)。
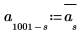
4. 将噪声的平均值设为零。
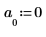
5. 使用 idft 函数得到傅立叶逆变换 (变换到时域)。
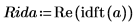
6. 绘制逆变换实数值的图像。
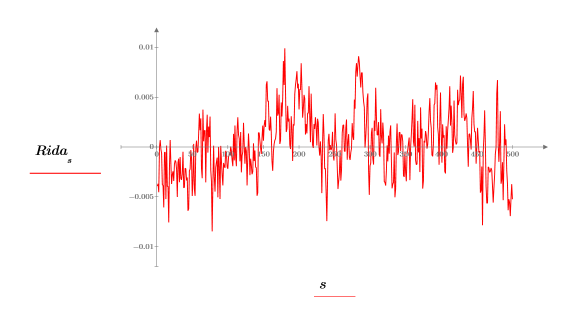
7. 使用 lcorr 函数来计算自相关曲线。
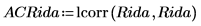
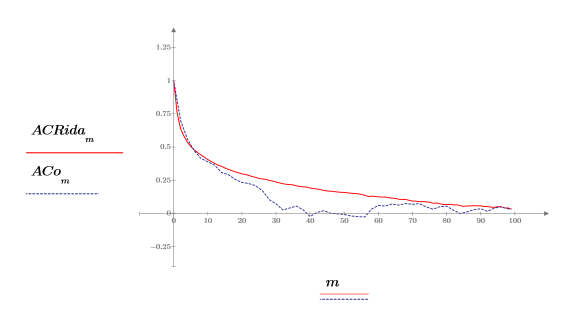
自相关行为与 onefn 的输出类似,0 处的相关系数为 1.0,其他点处的相关性有所不同。