示例:蒙特卡洛模拟
使用 montecarlo 函数生成可模拟函数的随机样本。
1. 定义要模拟的函数。
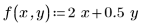
2. 定义每个参数的分布。
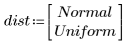
3. 定义每个分布的均值及标准差。将结果记录于矩阵 Rvals。
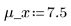 | 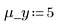 |
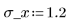 | 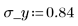 |
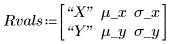
4. 设置参数 Y 的上限。
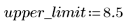
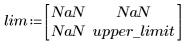
5. 定义所要生成的样本的数量。
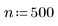
6. 调用 montecarlo 生成样本。
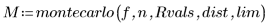
由 montecarlo 函数返回的输出是三列矩阵:
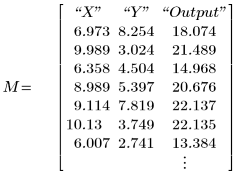
前两列是为每个参数所生成的样本。最后一列是函数 f 在这些参数下的输出。
7. 将生成的值记录到单独的矢量中。
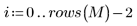 | 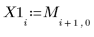 |
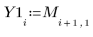 | 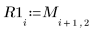 |
您可检查最后一个矢量 R1 是否确实为函数 f 的结果:
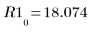
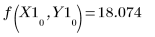
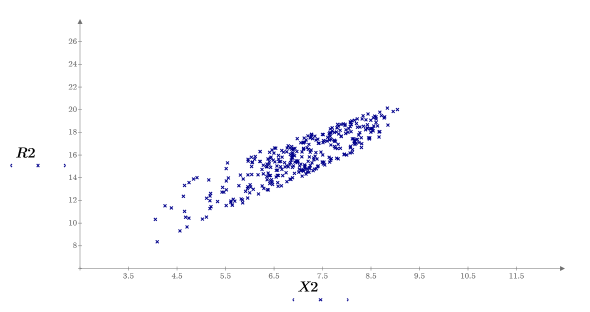
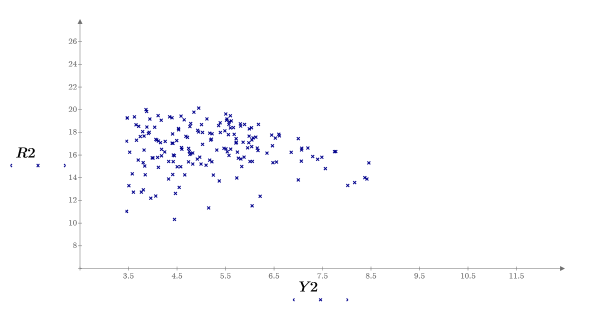
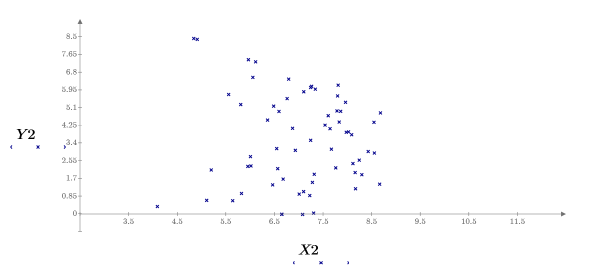
8. 绘制两者参数对比的图像并绘出其均值。
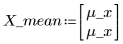 | 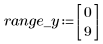 |
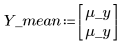 | 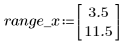 |
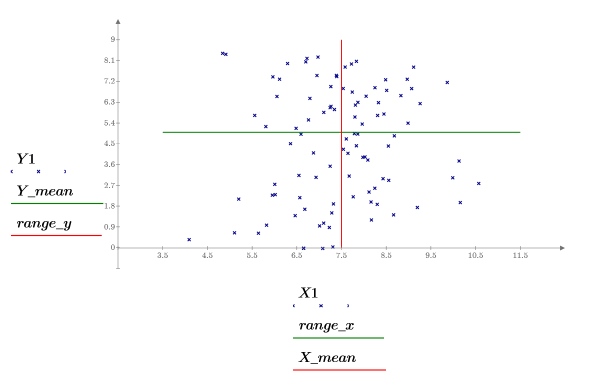
样本在 y 轴方向上均匀分布,而在 x 轴方向上正态分布。不会考虑 y 值大于 8.5 的样本。
y 值具有均匀的分布。在均值的两侧 6 个标准差范围之内生成样本:
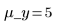
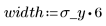
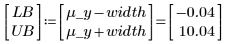
如果生成的样本大于上限,将不会被考虑:
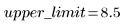
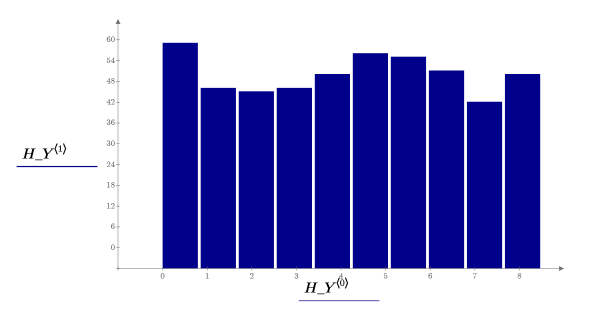
10. 调用 histogram 来将 x 值分为 10 个柱。绘制 y 值的柱状图,并添加正态分布图。
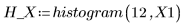
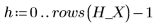
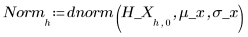
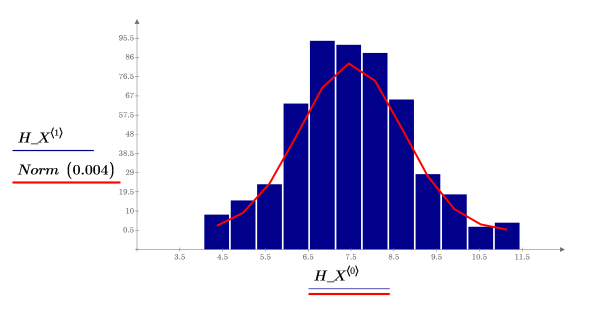
x 值符合正态分布。
11. 绘制每个参数结果的图像。
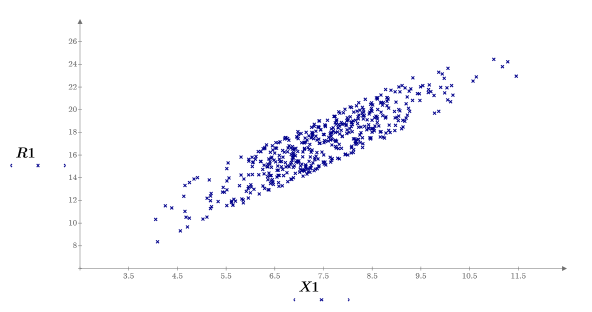
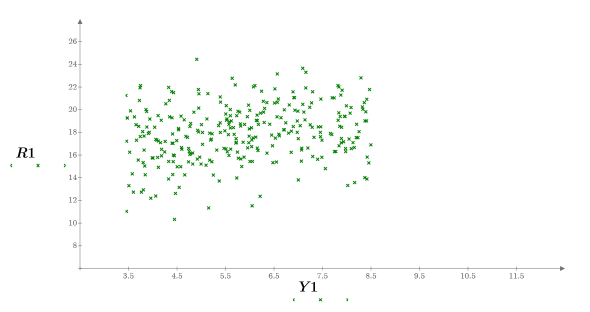
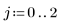
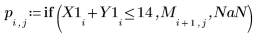
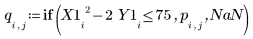
13. 一一绘制每个参数的图像。
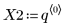
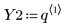
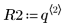
14. 绘制每个参数结果的图像。