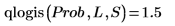示例:蒙特卡洛概率估计
生成随机数字来说明大采样方法如何估计分布未知的量的概率。
1. 使用位置和尺度参数 L 和 S 设置罗吉斯蒂分布的参数。
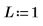
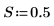
2. 设置蒙特卡洛采样参数。
◦ 要收集的单个样本数:
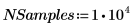
◦ 每个样本中的数据点数:
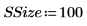
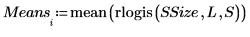
4. 估计一组随机数字的均值位于区间 [a, b] 内的概率。
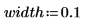
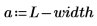
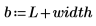
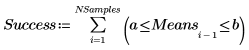
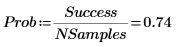
该概率取决于每个样本中的数据点数和区间宽度。
5. 绘制 plogis 函数以显示罗吉斯蒂分布的累积概率分布。使用水平标记来标记概率级别。
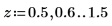
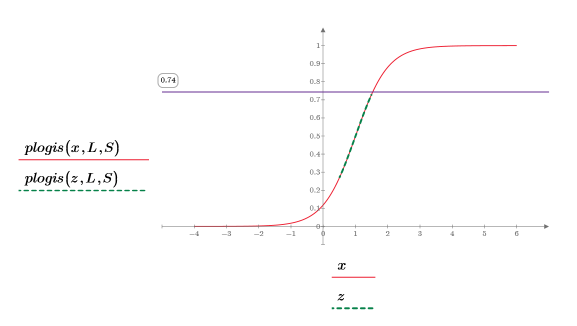
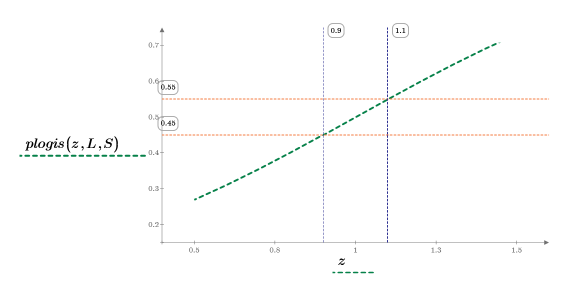
6. 缩放绘图的绿色虚线线段,然后使用竖直标记来标记 [a, b] 间隔并使用水平标记来标记 [a, b] 之间的下累积概率和上累积概率:
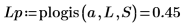
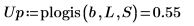
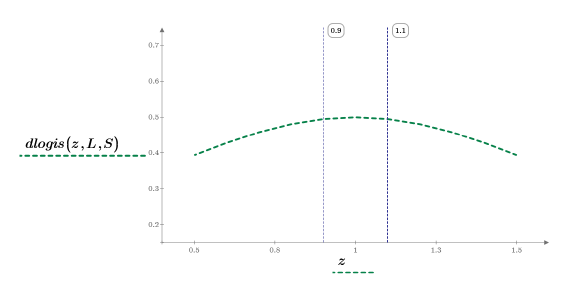
7. 绘制 dlogis 函数图像以显示罗吉斯蒂分布的概率密度。
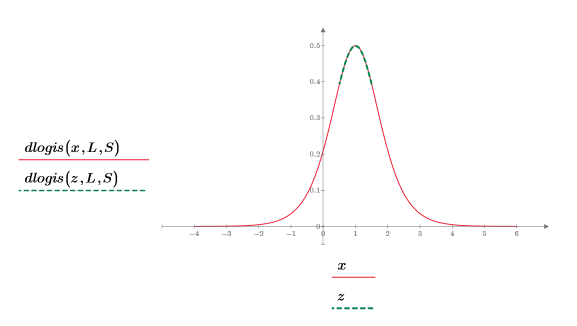
8. 缩放绘图的绿色虚线线段,然后使用竖直标记来标记 [a, b] 间隔: