示例：交互作用

使用 effects 函数了解交互作用在实验中的角色。

1. 使用 fullfact 函数来创建两个因子的设计矩阵。

<region id="ID0EYU3V" actualWidth="349.13" actualHeight="137.2" top="192.00000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="153">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">X</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">fullfact</id>
 <sequence>
 <real>2</real>
 <matrix rows="2" cols="1">
 <real>2</real>
 <real>3</real>
 </matrix>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

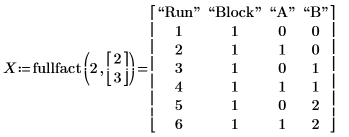
2. 在矩阵 Vals 中指定实验的实数值。Gender (性别) 因子分为 male (男性) 和 female (女性) 两个水平。Age (年龄) 因子分为 young (青年)、middle (中年) 和 old (老年) 三个水平。由于这两个因子具有的水平数量不同，因此将在 Vals 的第一行插入 NaN 以填充空元素。

<region id="ID0EUW3V" actualWidth="319.9666666666667" actualHeight="44.2" top="384.00000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="155">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Vals</id>
 <matrix rows="2" cols="4">
 <str xml:space="preserve">Gender</str>
 <str xml:space="preserve">Age</str>
 <str xml:space="preserve">Male</str>
 <str xml:space="preserve">Young</str>
 <str xml:space="preserve">Female</str>
 <str xml:space="preserve">Middle</str>
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">NaN</id>
 <str xml:space="preserve">Old</str>
 </matrix>
 </define>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

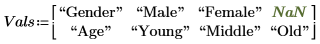
3. 使用 doelabel 函数根据 gender (性别) 和 age (年龄) 对实验结果进行排序。

<region id="ID0ETY3V" actualWidth="442.61333333333334" actualHeight="137.2" top="518.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="157">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">D</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">doelabel</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Vals</id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

矩阵 X 和 D 相同，但 X 显示因子的代码值而 D 显示其实际值。

无交互作用 - 仅有一个显著因子

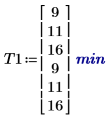
1. 记录各组在学习任务中花费的平均时间。对于 Run 1，青年男性的平均学习时间为 9 分钟。

2. 调用 effects 函数以查看 gender (性别)、age (年龄) 及其交互作用的效果。

<region id="ID0E433V" actualWidth="732.88333333333344" actualHeight="286" top="1056.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="161">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">effects</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">D</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <str xml:space="preserve">A, B, AB</str>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

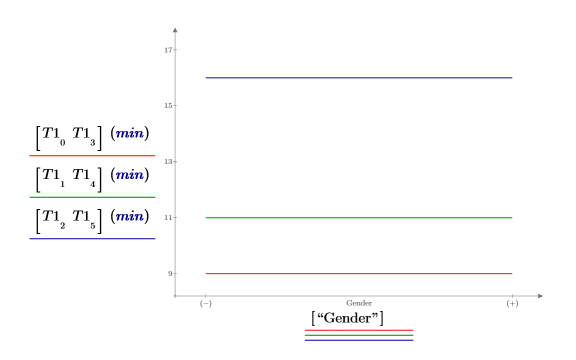
Gender 子矩阵证明 gender (性别) 不会影响学习时间。因此，不会报告 age (年龄) 和 gender (性别) 之间的交互作用效果。

3. 创建效果图以查看 age (年龄) 如何影响学习时间。最年轻的一组在学习任务中花费的平均时间为 9 分钟。

<region id="ID0EV53V" actualWidth="575.81538461538366" actualHeight="360" top="1324.8000000000002" left="38.400000000000006" height="360" width="575.81538461538366" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="163">
 <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">effects</traceStyle>
 </trace>
 <trace resultRef="164">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">effects</traceStyle>
 </trace>
 <trace resultRef="165">
 <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">effects</traceStyle>
 </trace>
 </traces>
 <graph-size width="383.815384615384" height="283.2" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-0.25" end="0.25">
 <axisLine position="bottom" positionticmark="-1" legendWidth="129.026666666667" />
 <axisGrid>
 <gridFrequency>3</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="166">
 <matrix rows="1" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <str xml:space="preserve">Gender</str>
 </matrix>
 </math>
 <math resultRef="167">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="9" end="17">
 <axisLine position="left" positionticmark="-1" legendWidth="147.196666666667" />
 <axisGrid>
 <gridFrequency>5</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="174">
 <matrix rows="1" cols="2" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <real>0</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <real>3</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="175">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="176">
 <matrix rows="1" cols="2" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <real>1</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <real>4</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="177">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="178">
 <matrix rows="1" cols="2" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <real>2</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T1</id>
 <real>5</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="179">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="169">
 <real xmlns="http://schemas.mathsoft.com/math50">9</real>
 </startValue>
 <secondTickValue resultRef="171">
 <real xmlns="http://schemas.mathsoft.com/math50">11</real>
 </secondTickValue>
 <endValue resultRef="173">
 <real xmlns="http://schemas.mathsoft.com/math50">17</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

无交互作用 - 有两个显著因子

1. 记录各组在学习第二个任务中花费的平均时间。

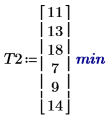
2. 调用 effects 函数以查看 gender (性别)、age (年龄) 及其交互作用的效果。

Age (年龄) 对学习过程的影响与对第一个任务的影响相同。但此次 male (男性) 在学习任务中花费的时间要比 female (女性) 多。

3. 要计算 AB 在 A 和 B 不同水平处的交互作用效果，可将 i 和 j 定义为 A 和 B 的水平，将 mABi, j 定义为 AB 在 i 和 j 处的平均响应。

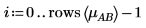
4. 使用 mean 函数来计算此实验的整体平均时间以及各个因子的平均时间。

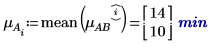
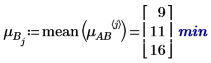
5. 计算每个因子的水平效果。

6. 针对 A 和 B 的因子水平，使用 augment 函数计算累加因子效果，这些效果为总体实验均值，即针对 A 和 B 的各个水平的 A 水平效果与 B 水平效果之和。

<region id="ID0ESO4V" actualWidth="421.13" actualHeight="46.110000000000007" top="3052.8000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="213">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Additive</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve">augment</id>
 <sequence>
 <apply>
 <plus />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <real>0</real>
 </apply>
 </apply>
 <apply>
 <plus />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <real>1</real>
 </apply>
 </apply>
 <apply>
 <plus />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <real>2</real>
 </apply>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <id labels="UNIT" xml:space="preserve">min</id>
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

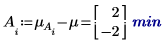
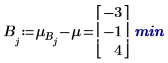
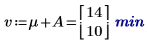
7. 计算交互作用效果，或 AB 的平均响应与 A 和 B 每个水平的累加因子效果之间的差值。

<region id="ID0EOQ4V" actualWidth="210.62" actualHeight="44.2" top="3148.8000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="215">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <minus />
 <id labels="VARIABLE" xml:space="preserve">
 μ<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">AB</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Additive</id>
 </apply>
 <unitOverride>
 <id labels="UNIT" xml:space="preserve">min</id>
 </unitOverride>
 </eval>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

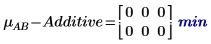
对于本任务，age (年龄) 与 gender (性别) 之间不存在交互作用效果。

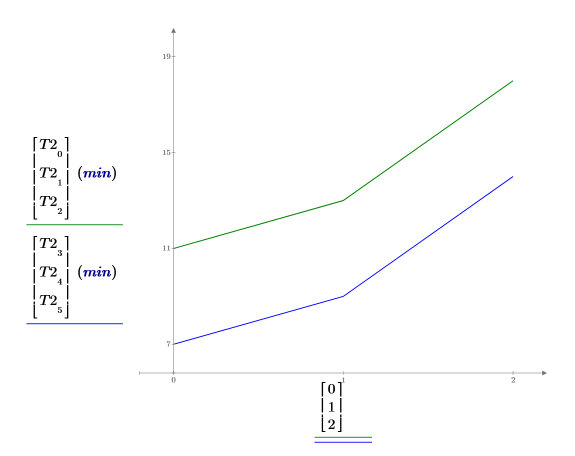
8. 绘制每种 gender (性别) 平均学习时间的图像。青年女性在学习第二个任务中花费的平均时间为 7 分钟。因为 gender (性别) 和 age (年龄) 之间不存在交互作用效果，因此两条曲线平行。

<region id="ID0ECS4V" actualWidth="575.38461538461445" actualHeight="456" top="3283.2000000000003" left="38.400000000000006" height="456" width="575.38461538461445" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="217">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="218">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="421.784615384614" height="360" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="2">
 <axisLine position="bottom" positionticmark="-1" legendWidth="75.5366666666667" />
 <axisGrid>
 <gridFrequency>3</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="221">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <real>0</real>
 <real>1</real>
 <real>2</real>
 </matrix>
 </math>
 <math resultRef="222">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="220">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="7" end="19">
 <axisLine position="ticknumberlock" positionticmark="0" legendWidth="115.696666666667" />
 <axisGrid>
 <gridFrequency>4</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="229">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T2</id>
 <real>0</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T2</id>
 <real>1</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T2</id>
 <real>2</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="230">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="231">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T2</id>
 <real>3</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T2</id>
 <real>4</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T2</id>
 <real>5</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="232">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="224">
 <real xmlns="http://schemas.mathsoft.com/math50">7</real>
 </startValue>
 <secondTickValue resultRef="226">
 <real xmlns="http://schemas.mathsoft.com/math50">11</real>
 </secondTickValue>
 <endValue resultRef="228">
 <real xmlns="http://schemas.mathsoft.com/math50">19</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

具有重要的交互作用

1. 记录各组在学习第三个任务中花费的平均时间。调用 effects 函数以查看 gender (性别)、age (年龄) 及其交互作用的效果。

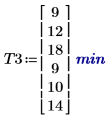
age (年龄) 对第一个和第二个任务的影响相同，但 gender (性别) 对第二个任务的影响较小。对于第三个任务，age (年龄) 和 gender (性别) 之间存在交互作用效果。

2. 计算交互作用效果。

3. 使用 mean 函数来计算此实验的整体平均时间以及各个因子的平均时间。

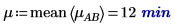
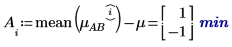
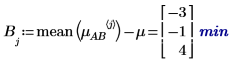
4. 针对 A 和 B 的因子水平，使用 augment 函数计算累加因子效果，这些效果为总体实验均值，即针对 A 和 B 的各个水平的 A 水平效果与 B 水平效果之和。

<region id="ID0EB24V" actualWidth="500.18000000000006" actualHeight="46.110000000000007" top="4742.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="255">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Additive</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve">augment</id>
 <sequence>
 <apply>
 <plus />
 <apply>
 <plus />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">μ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <real>0</real>
 </apply>
 </apply>
 <apply>
 <plus />
 <apply>
 <plus />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">μ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <real>1</real>
 </apply>
 </apply>
 <apply>
 <plus />
 <apply>
 <plus />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">μ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
 <real>2</real>
 </apply>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <id labels="UNIT" xml:space="preserve">min</id>
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

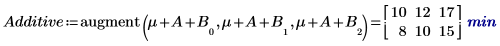
5. 计算交互作用效果，或 AB 的平均响应与 A 和 B 每个水平的累加因子效果之间的差值。

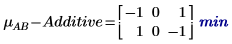
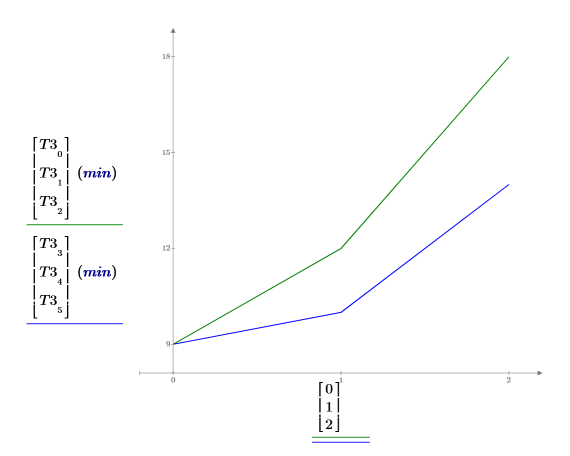
交互作用 AB 的平均响应与累加因子效果之间存在差值。

6. 绘制每种 gender (性别) 平均学习时间的图像。虽然青年男性和青年女性之间的完成时间一样，但老年男性学习第三个任务花费的时间要比老年女性长。两条曲线不平行，因为 age (年龄) 和 gender (性别) 之间存在重要的交互作用。

<region id="ID0EW54V" actualWidth="569.99999999999909" actualHeight="456" top="5030.4000000000005" left="38.400000000000006" height="456" width="569.99999999999909" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="259">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="260">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="416.399999999999" height="360" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="2">
 <axisLine position="bottom" positionticmark="-1" legendWidth="75.5366666666667" />
 <axisGrid>
 <gridFrequency>3</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="263">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <real>0</real>
 <real>1</real>
 <real>2</real>
 </matrix>
 </math>
 <math resultRef="264">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="262">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="9" end="18">
 <axisLine position="origin" positionticmark="0" legendWidth="115.696666666667" />
 <axisGrid>
 <gridFrequency>4</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="269">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T3</id>
 <real>0</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T3</id>
 <real>1</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T3</id>
 <real>2</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="270">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="271">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T3</id>
 <real>3</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T3</id>
 <real>4</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T3</id>
 <real>5</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="272">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="266">
 <real xmlns="http://schemas.mathsoft.com/math50">9</real>
 </startValue>
 <secondTickValue resultRef="268">
 <real xmlns="http://schemas.mathsoft.com/math50">12</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

具有不重要的交互作用

1. 记录各组在学习第四个任务中花费的平均时间。

2. 调用 effects 函数以查看 gender (性别)、age (年龄) 及其交互作用的效果。

<region id="ID0EHC5V" actualWidth="732.88333333333344" actualHeight="286" top="5875.2000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="284">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">effects</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">D</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <str xml:space="preserve">A, B, AB</str>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

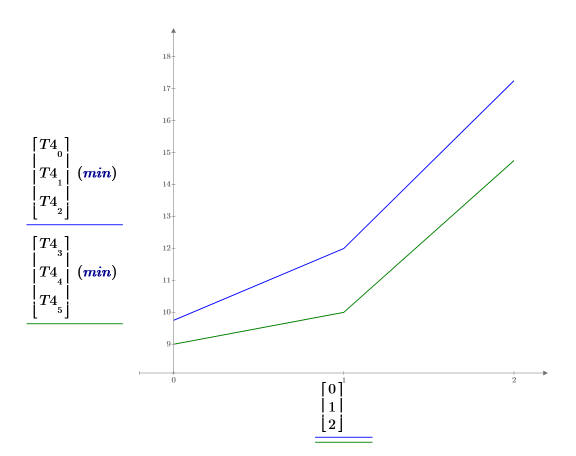
Gender (性别) 和 age (年龄) 的影响对第三个任务的影响非常相似。

3. 绘制每种 gender (性别) 平均学习时间的图像。两条曲线几乎平行，表示尽管 age (年龄) 和 gender (性别) 之间存在交互作用，但此交互作用并不重要。

<region id="ID0E2D5V" actualWidth="576.38461538461445" actualHeight="456" top="6124.8000000000011" left="38.400000000000006" height="456" width="576.38461538461445" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="286">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="287">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="422.784615384614" height="360" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="2">
 <axisLine position="bottom" positionticmark="-1" legendWidth="75.5366666666667" />
 <axisGrid>
 <gridFrequency>3</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="290">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <real>0</real>
 <real>1</real>
 <real>2</real>
 </matrix>
 </math>
 <math resultRef="291">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="289">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="9" end="18">
 <axisLine position="origin" positionticmark="0" legendWidth="115.696666666667" />
 <axisGrid>
 <gridFrequency>10</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="294">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <real>0</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <real>1</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <real>2</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="295">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="296">
 <matrix rows="3" cols="1" xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <real>3</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <real>4</real>
 </apply>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">T4</id>
 <real>5</real>
 </apply>
 </matrix>
 </math>
 <math resultRef="297">
 <id labels="UNIT" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="293">
 <real xmlns="http://schemas.mathsoft.com/math50">10</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

参考文献

Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4th ed., McGraw-Hill/Irwin, Boston, 1996, pp. 803.