示例:标识有影响的观察值
使用函数 polyfitstat 测试用于创建多变量多项式回归的观察值。
1. 定义一个矩阵,其中包含取自 25 至 34 岁之间 20 个健康个人的示例。
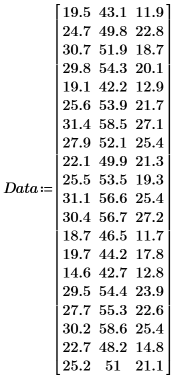
矩阵的列分别表示这 20 个人中每个人的三头肌皮皱厚度、大腿围和体脂含量。
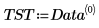
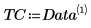
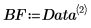
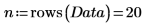
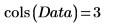
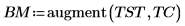
4. 调用 polyfitstat 利用一阶回归法模拟该实验,并计算回归统计。
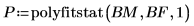
5. 显示在输出矩阵 P 的第 7 行中得到的回归系数矩阵。
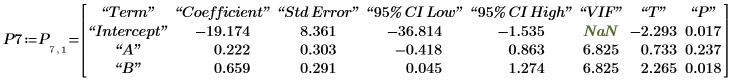
6. 使用矩阵运算计算回归系数。
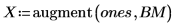
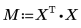
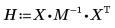
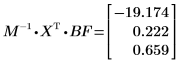
回归系数满足下列方程:
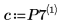
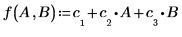
7. 使用回归方程计算预测的体脂肪含量。将这些值与所测得的体脂肪含量进行对比。
 |  |
8. 使用 submatrix 函数显示输出矩阵 P 第一行中的模型统计。

第一个统计数据是回归的标准差。
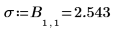
9. 显示在输出矩阵 P 的最后一个嵌套矩阵中得到的模型诊断数据。
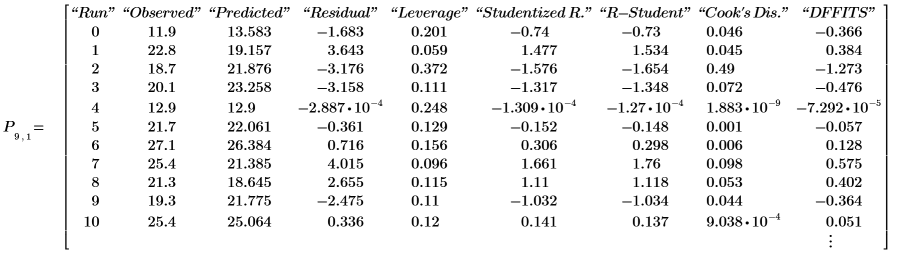
上图中的观察值和预测值对应于步骤 7 中所显示的值。残差是观察值与预测值之间的差值:
10. 计算残差或观察值与预测值之差。
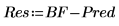
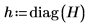
12. 计算学生化残差。
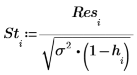
外部学生化残差或 R-student 计算如下。常数 p 为所计算的回归系数的数值,而 S2 为 s2 的估值 (基于已移除的第 i 个观察值的数据集)。
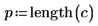
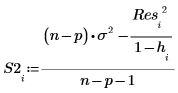
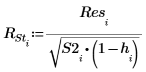
13. 使用 Cook 距离测量已删除点对线性回归的总体影响。
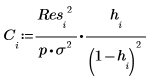
14. 计算当拟合包含所有观察值时的预测值和省略第 i 个观察值时的预测值之间的差值
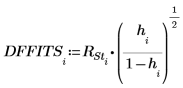
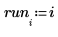
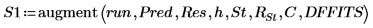
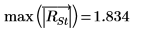
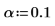
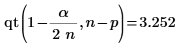
最大的 R-student 值小于邦弗朗尼检验则表明相应的观察值不是离群值。
17. 确定最大 DFFITS 值。
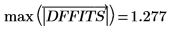
该值大于 1,但非常接近 1,因此对应的观察值未必有影响。
18. 通过绘制“Cook 距离-游程”图像,创建索引影响图。
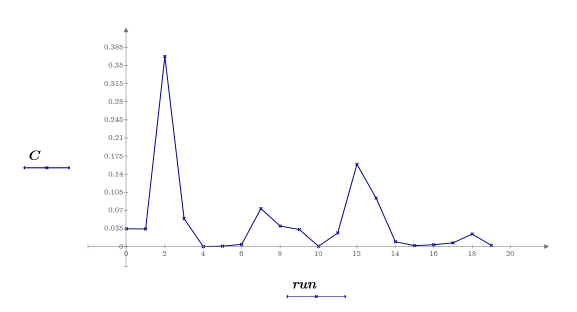
run2 观察值是数据集中最具影响的观察值。步骤 10 中得出的 run12 观察值也具有影响,但比 run2.观察值的影响小得多。
参考文献
参考:Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4th ed., McGraw-Hill/Irwin, Boston, 1996, pp. 375