示例:傅立叶变换对
定义信号的周期、采样频率以及样本数。
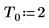 |
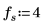 |
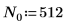 |
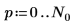 |
正弦信号
1. 使用符号运算求出正弦信号的傅立叶变换。
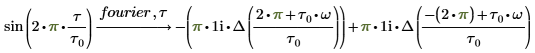
重排结果项得到:
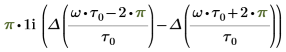
结果显示了两个涉及 Dirac delta (单位脉冲) Δ 函数的分量。
2. 使用 sin 函数来定义正弦信号:
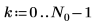
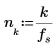
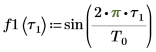
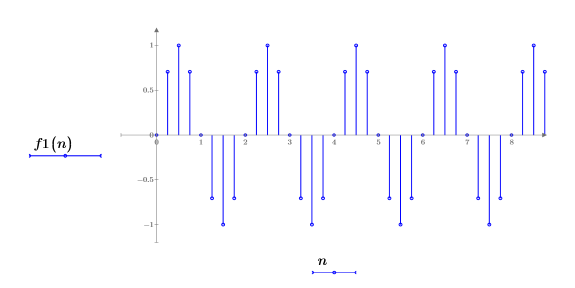
3. 绘制函数 f1 前几个元素的图像。
4. 使用函数 dft 求出信号的离散傅立叶变换。
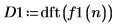
5. 绘制函数傅立叶变换的两个分量的图像。使用竖直标记显示它们相对于采样频率出现的位置。
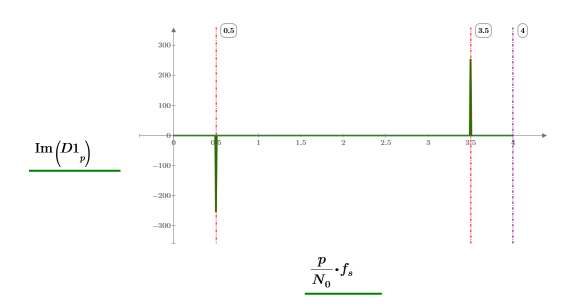
方形脉冲 (方脉冲) 信号
1. 使用海维赛德阶梯函数 Φ 来定义方形脉冲信号。
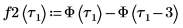
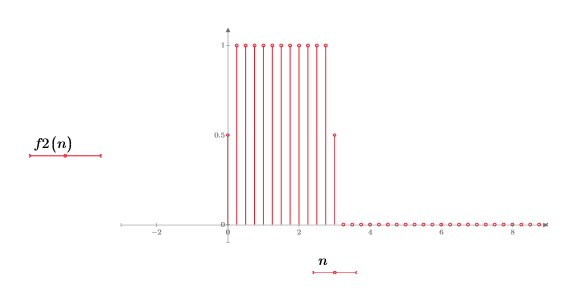
2. 绘制函数 f2 前几个元素的图像。
3. 使用 dft 函数求出方形脉冲信号的离散傅立叶变换。
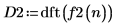
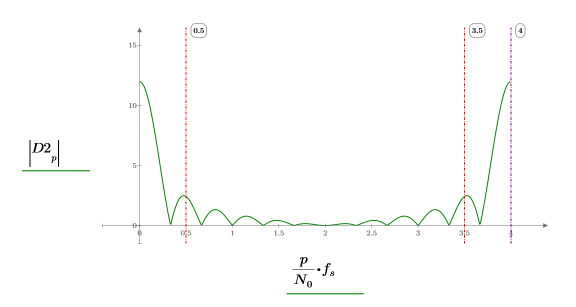
4. 绘制方形脉冲信号的傅立叶变换。使用竖直标记显示它们相对于采样频率出现的位置。
高斯信号
1. 定义以下高斯信号。
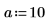
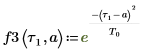
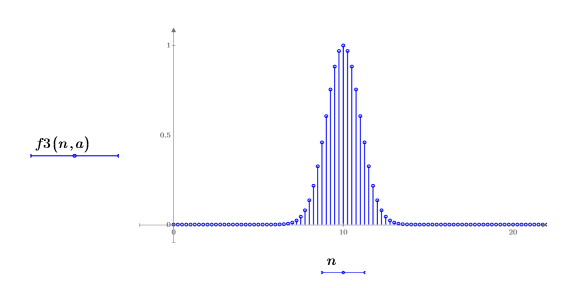
2. 绘制函数 f3 前几个元素的图像。
3. 使用函数 dft 求出高斯信号的离散傅立叶变换。
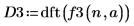
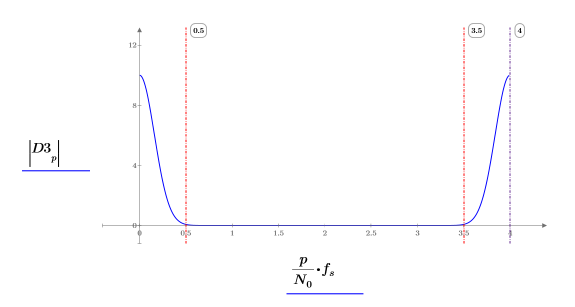
4. 绘制高斯信号傅立叶变换的图像。使用竖直标记显示它们相对于采样频率出现的位置。