示例：离散余弦变换

函数 > 图像处理 > 变换域 > 示例：离散余弦变换

示例：离散余弦变换

使用 dct 和 idct 函数可分别计算离散的余弦变换与逆变换。该变换的优点在于可将大部分图像“能量”或信息集中到某些频率分量中，非常适用于编码操作。

有关使用此示例的信息，请参考关于图像处理示例。

1. 定义大小为 N x P 的矩阵 M。

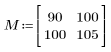
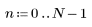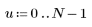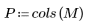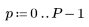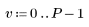2. 余弦变换的实现使用 II 型 DCT。将 DCT 定义为此变换的解析式。

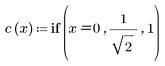
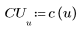
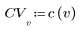
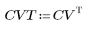
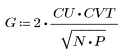
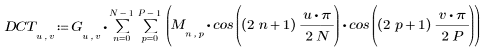
3. 计算矩阵 DCT。

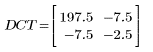
4. 将函数 dct 应用于矩阵 M。

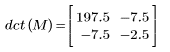
5. 计算 DCT 和 dct 函数之间的最大误差。

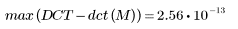
能量压缩

余弦变换具有很好的能量压缩属性，这意味着它可将大部分能量集中到变换的前几个系数上。

1. 定义输入矩阵。

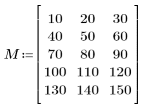
2. 将函数 dct 应用于矩阵 M 并对其进行计算。

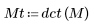
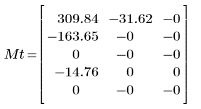
生成的矩阵显示大部分与系数值相关的能量都集中在前几个系数上。

idct

反函数用于从变换恢复原始图像。

1. 读取黑白版的蒙娜丽莎图像。

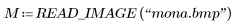
(mona.bmp)

2. 应用 dct 函数来变换图像。

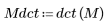
(mona_noise.bmp)

3. 应用反函数来恢复图像。

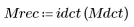
(mona_rec.bmp)

4. 通过查看变换后的图像和原始图像的柱状图验证 DCT 的能量压缩属性。

<region id="ID0EBMIZ" top="3000" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">H</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">Horig</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

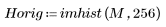
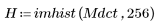
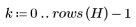
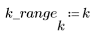
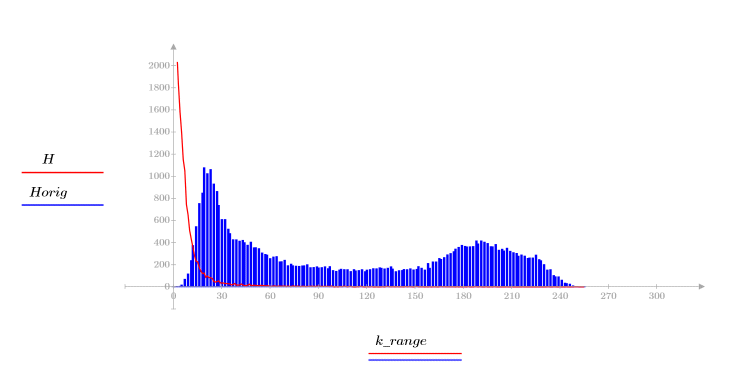
变换后的图像将大部分能量集中到了柱状图的前几个柱上，而原始图像的能量分布则是分散的。这使变换后的图像更适合编码或传输，因为使用较少的频率分量即可传送大部分图像信息。因此，DCT 可用于图像压缩。