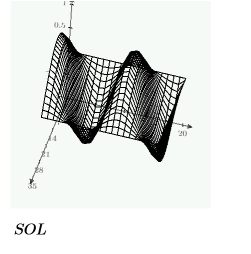
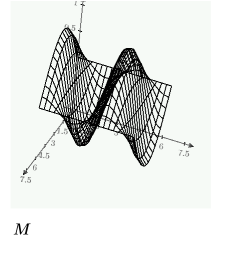
示例:求解命令块中的 PDE
使用求解命令块中的偏微分方程 (PDE) 和偏微分方程求解器 numol 比较波方程的解。
PDE 求解命令块
要求解下列一维波方程:
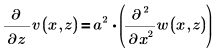
使用约束:
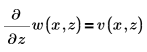
要将第一个方程转换为由两个偏微分方程组成的方程组,请设置 PDE 求解命令块
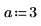
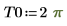
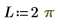
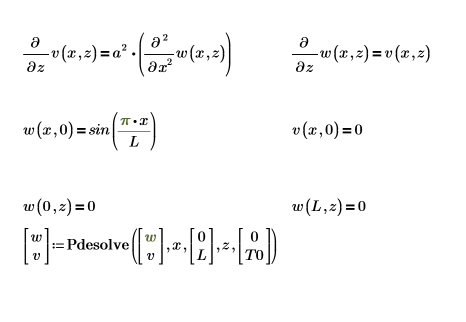
以下是边界上的一个解:
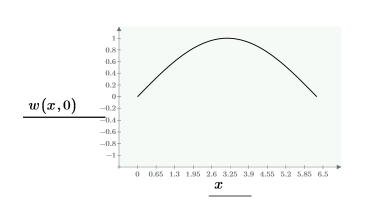
使用上面定义的约束,创建要通过 CreateMesh 函数三维绘制的解网格:
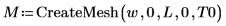
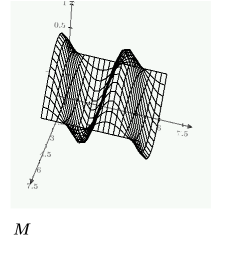
使用 numol
可求解命令行求解器 numol。当希望在程序中包含计算时,该求解器十分有用。
定义系统中偏微分方程和代数约束的数量:
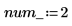
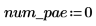
用于计算 PDE 右侧的函数是长度为 num_pde + num_pae 的矢量 (偏代数方程)。此时的函数为一方程组。类似地,边界条件被定义成长度为 num_pde + num_pae 的列矢量。
PDE 矢量的表达式:
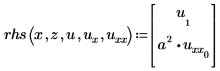
如上定义,u1=v 且 u0=w。
含初始条件值的向量:
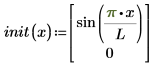
假设每个左侧均为未知函数矢量 u 的一阶时间导数。函数的变量为 x (空间) 和 t (时间)。解为 u,也可以是由方程组的解构成的矢量:ux (矢量中每个解 u 的一阶导数) 和 uxx (二阶空间导数)。
必须使用矢量下标来标记 u 中的各个条目,ux 和 uxx。
边界条件的矢量可具有三种类型的行。每一行由下列内容之一确定:
• rhs 包含二阶空间导数:需要两个边界条件 (Dirichlet "D" 或 Neumann "N"),积分区域每侧各一个。
• rhs 包含一阶空间导数:一个用于积分区域左侧或右侧的 Dirichlet 边界条件,另一个条件为 "NA"。
• 如果矢量不包含空间导数,则无需边界条件。
左右边界的边界条件遵循以下约定:
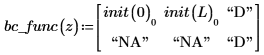
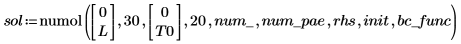
numol 的结果为一矩阵,该矩阵将空间中的每个点表示为行,将时间中的每个点表示为列。这样一来便可每次拾取一列,同时在单个时间点显示整个空间中的解,从而便于解的可视化。求解方程组时,会将每个未知函数的解矩阵附加到前一矩阵的一侧。
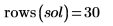
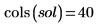
在当前示例中,每个函数有 20 个时间点,因此矩阵包括 40 个列。拾取第一个解 u0:
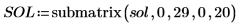
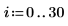
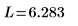
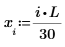
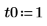
比较 numol 和 Pdesolve
在点 t0 比较解 numol 和 Pdesolve:
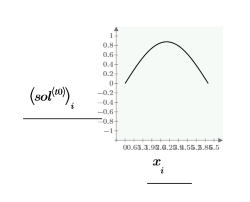
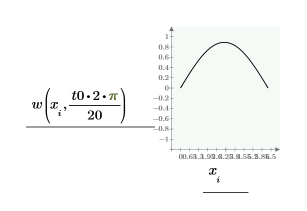
比较空间和时间值的解网格: