ODE 함수
• odesolve(vf, b, [intvls]) - 초기치나 경계값 제약 조건에 따라 상미분 방정식(ODE) 시스템에 대한 해를 나타내는 함수를 정의합니다. ODE는 최고차 도함수 항에서 선형이 되어야 하며 초기 조건 및 경계 조건의 수는 ODE의 차수와 동일해야 합니다.
인수
• vf는 함수이거나 풀이 구간 내에 나타나는 함수의 열 벡터입니다.
vf에서 함수를 정의할 때 인수 목록을 포함시켜야 합니다. 예를 들어, f(t) 및 g(t) 함수를 풀이할 경우 vf를 다음과 같이 입력합니다.
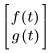
• b는 적분 구간의 끝점(실수)입니다. b는 풀이 구간에 정의된 초기치보다 크거나 작을 수 있습니다.
• intvls(선택 사항)는 풀이 함수를 보간하는 데 사용되는 이산화 간격의 수(정수)입니다. 해 점의 수는 intervals + 1입니다. intvls의 기본값은 1000입니다.
대개 intvls의 기본값은 정확한 보간 해를 얻는 데 충분하지만 이 값을 늘려 더 정확한 해를 얻을 수 있습니다. 이렇게 할 경우 odesolve에서 보간을 위해 더 많은 점을 저장해야 하므로 계산 시간이 늘어날 수 있습니다.
큰 구간에 걸쳐 ODE를 푸는 경우에는 intvls를 기본값보다 큰 값으로 설정해야 합니다.
단위 및 차원
odesolve 함수와 제약 조건에 단위를 사용할 수 있습니다. 단위 및 차원에는 다음 규칙이 적용됩니다.
• 풀이 과정 전체에 걸쳐 일관적인 차원을 사용해야 합니다. t가 argumentDimension이고 f(t)가 valueDimension인
경우에는
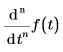 의 차원은 valueDimensions/argumentDinemsionsn이어야 합니다.
의 차원은 valueDimensions/argumentDinemsionsn이어야 합니다.예: t가 초 단위이고 f(t)가 미터 단위인 경우
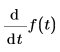 의 단위는 m/s이고
의 단위는 m/s이고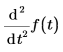 의 단위는 m/s2입니다.
의 단위는 m/s2입니다.• 적분 구간의 초기치와 끝점은 함수 인수와 같은 차원이어야 합니다.
• 이산화 구간의 수에는 항상 단위가 없습니다.
추가 정보
• 함수 odesolve는 풀이 구간 내에서만 사용할 수 있습니다.
• 기존 PTC Mathcad 함수 Odesolve는 해당 소문자 함수와 상호 교환하여 사용할 수 있습니다.
• 리본 메뉴에서 소문자 함수를 삽입하거나 수동으로 소문자/대문자 버전을 입력하면 자동으로 키워드 레이블이 할당됩니다.
• odesolve 함수에서는 Adams/BDF 풀이 알고리즘을 사용합니다.
• 풀이 구간 내에서 odesolve는 TOL 값의 영향을 받지 않습니다.