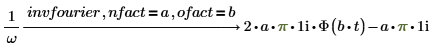예제: 기호 변환
기호 푸리에, 라플라스 및 Z 변환과 각각의 역 변환을 수행합니다.
푸리에 및 역 푸리에 변환
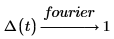
예상대로 이 변환은 상수 주파수를 반환합니다.
2. 헤비사이드 계단 함수 Φ를 포함하는 함수의 푸리에 변환을 구합니다.
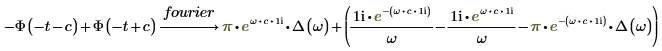
3. simplify 키워드를 추가하여 결과를 단순화합니다.
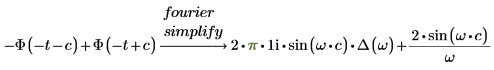
Z 및 역 Z 변환
1. ztrans 키워드를 사용하여 다음 두 함수의 Z 변환을 계산합니다.
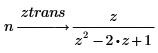
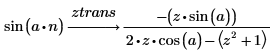
2. invztrans 키워드를 사용하여 다음 두 함수의 역 Z 변환을 계산합니다.
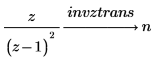
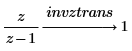
변환의 기본 변수 변경
1. 함수의 역 라플라스를 구합니다.
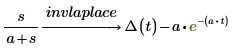
2. transform 키워드 이후에 한 쌍의 인수를 추가하여 역 라플라스 변환에서 구한 함수의 기본 변수 t를 변경합니다.
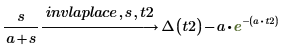
◦ 첫 번째 인수 s는 정의역 함수의 독립 변수입니다.
◦ 두 번째 인수 t2는 변환된 함수의 새 독립 변수입니다.
◦ 반환된 역 라플라스 변환에서는 변수 t2를 독립 변수로 사용합니다. Δ는 디락 델타 함수입니다.
◦ Δ는 수치 등호를 사용하여 계산할 수 없지만 기호 연산 연산자를 사용하여 계산할 수 있습니다.
3. laplace 키워드를 사용하여 결과의 라플라스 변환을 구합니다.
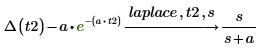
한 번에 여러 개의 키워드 사용
기호 계산의 결과가 원하는 형태가 아닌 경우 변환 키워드 이후에 키워드를 추가하여 결과의 형식을 수정할 수 있습니다.
1. 함수의 Z 변환을 구합니다.
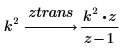
2. expand 키워드를 사용하여 결과를 전개합니다.
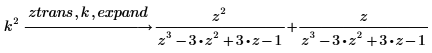
3. laplace 키워드를 사용하여 함수의 라플라스 변환을 구합니다.
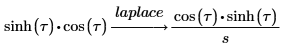
4. simplify 키워드를 사용하여 결과의 단순화된 형태를 얻습니다.
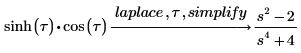
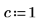
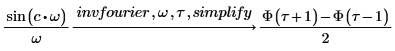
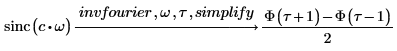
기호 변환이 없는 입력 함수의 경우 수치 dft 함수를 사용합니다.
푸리에 변환 인수 분해
1. nfact 및 ofact와 fourier를 표현식에 추가합니다.
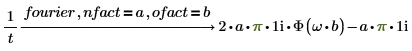
2. nfact 및 ofact와 invfourier를 표현식에 추가합니다.