예제: 상태 공간 풀이 시스템
풀이 시스템 statespace를 사용하여 1차 상미분 방정식(ODE)의 상태 공간 표현을 풀이합니다.
구체적으로, 조화 진동 방정식의 우변이 0인 비강제 조화 진동기의 경우에 대한 풀이를 구합니다.
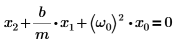
해에는 과감쇄 해, 임계 감쇄 해, 부족 감쇄 해, 전체 상태 피드백 해의 네 가지 사례가 있습니다. |
과감쇄 해
1. 과감쇄 해에 대한 수학 방정식을 작성합니다.
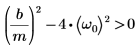
2. 초기 조건, 물체의 질량, 감쇄 상수, 적분 구간의 시작과 끝, 점 수를 정의합니다.
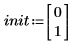
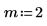
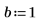
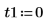
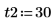
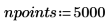
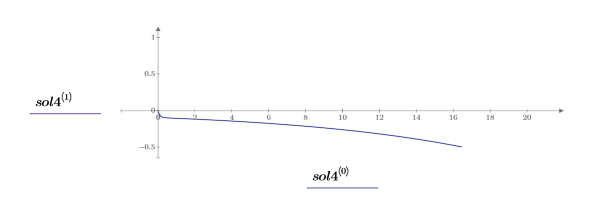
3. 시스템의 고유 진동수나 공명 진동수를 설정합니다.
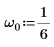
4. 과감쇄 조건이 존재하는지 확인합니다.
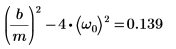
5. 행렬 형태로 ODE를 작성합니다.
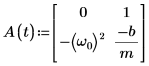
6. statespace 함수를 호출합니다.
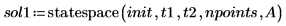
7. 해를 도표화합니다.
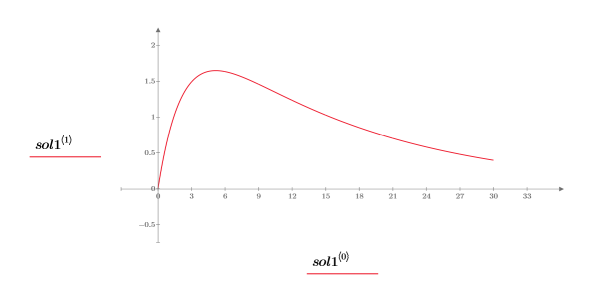
임계 감쇄 해
1. 시스템의 고유 진동수나 공명 진동수를 설정합니다.
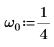
2. 임계 감쇄 조건이 존재하는지 확인합니다.
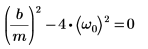
3. 행렬 형태로 ODE를 작성합니다.
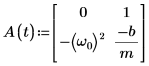
4. statespace 함수를 호출합니다.
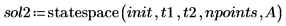
5. 해를 도표화합니다.
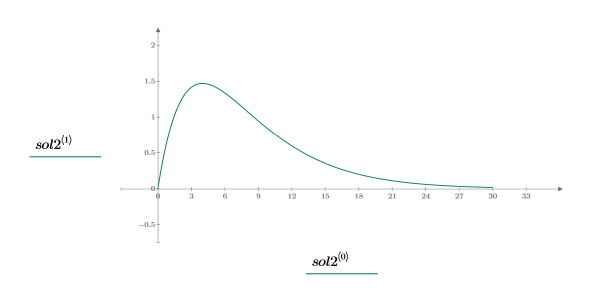
부족 감쇄 해
1. 시스템의 고유 진동수나 공명 진동수를 설정합니다.
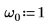
2. 부족 감쇄 조건이 존재하는지 확인합니다.
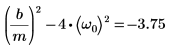
3. 행렬 형태로 ODE를 작성합니다.
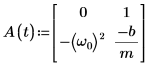
4. statespace 함수를 호출합니다.
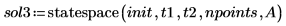
5. 해를 도표화합니다.
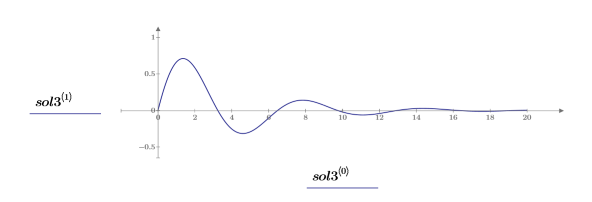
전체 상태 피드백 해
1. 초기 조건을 설정합니다.
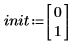
2. 행렬 형식으로 ODE를 작성합니다.
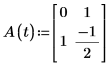
3. 추가 함수를 정의합니다.
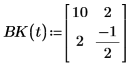
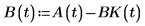
4. statespace 함수를 호출합니다.
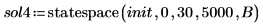
5. 해를 도표화합니다.