예제: 정사각형 강판의 열 흐름

함수 > 풀이 및 최적화 > 미분 방정식 풀이 > 예제: 정사각형 강판의 열 흐름 - II

예제: 정사각형 강판의 열 흐름 - II

편미분 방정식 풀이 시스템 relax를 사용하여 정사각형 강판의 정상 상태 온도 분포를 풉니다.

포아송 방정식 풀이

열원 함수의 값이 알려져 있으며 경계 조건이 0이 아닌 위치에서 열 방정식을 풉니다.

relax 함수는 완전히 다른 풀이 방식에 기반하므로 다른 인수 집합이 필요합니다.

1. 라플라스(Laplace) 근사 계수를 포함하는 정방 행렬 다섯 개(a, b, c, d 및 e)를 정의합니다.

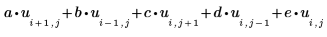
이러한 행렬은 원하는 크기로 지정할 수 있습니다. 행렬이 클수록 해의 메쉬가 세밀해집니다.

2. 정사각형 강판의 치수를 정의합니다.

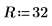
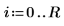
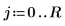
3. 계수를 정의합니다.

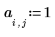
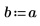
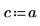
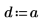
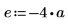
4. 상수 열원의 강도와 위치를 정의합니다.

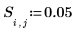
5. 격자선 크기와 동일한 크기이며 함수 F(x,y)의 알려진 경계 값과 알려지지 않은 내부 값에 대한 추측값을 포함하는 정방 행렬 f를 정의합니다.

◦ 상부의 경계 조건:

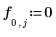
◦ 하부의 경계 조건:

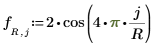
◦ 가장자리의 경계 조건:

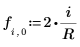
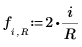
6. 0과 1 사이의 실수인 Jacobi spectral radius 변수 r를 정의합니다.

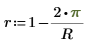
이 매개변수는 알고리즘의 수렴을 제어합니다. "반복이 너무 많습니다"라는 오류 메시지가 나타나면 r를 줄여 보십시오.

7. relax 함수를 호출합니다.

<region id="ID0EFM25" top="1516.8000000000002" left="38.400000000000006" height="25.6" width="204.10333333333335" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">F</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">relax</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">c</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">e</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">f</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">r</id>
        </sequence>
      </apply>
    </define>
  </math>
</region>

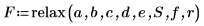
8. 정사각형 강판의 열 분포를 표시하는 3D 도표를 생성합니다.

<region id="ID0EVN25" top="1747.2000000000003" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="32" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-3" end="4.5">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">F</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.052623873051966662</Cell>
          <Cell>0.043294250885890617</Cell>
          <Cell>0.99767546618388891</Cell>
          <Cell>0</Cell>
          <Cell>0.095704097834471175</Cell>
          <Cell>0.99467978821191028</Cell>
          <Cell>-0.038116198399097093</Cell>
          <Cell>0</Cell>
          <Cell>-0.99401783366431629</Cell>
          <Cell>0.093475808436936883</Cell>
          <Cell>-0.056487340124674094</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthographic</CameraType>
    </plot3D>
  </plot>
</region>

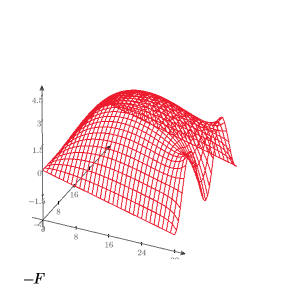
9. 등온도선을 표시하는 등고선도를 생성합니다.