예제: 회로의 감쇄 조화 진동
저항 R, 인덕터 L 및 커패시터 C가 포함된 간단한 전기 회로를 가정합니다.
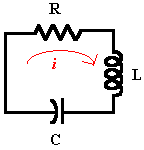
미분 방정식을 사용하여 커패시터 C의 전하 Q를 모델링한 다음 ODE 풀이 함수를 사용하여 나머지 근사해를 구합니다. 마지막으로 결과를 정확한 해 Q와 비교합니다.
미분 방정식 사용
1. 세 개의 컴포넌트를 지나는 전압에 대한 미분 방정식을 작성합니다. 이 전압은 최종적으로 0이 되어야 합니다.
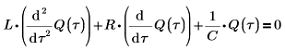
2. 축전기 C에서 전하 Q의 순간적인 변화를 나타내는 미분 방정식을 작성합니다.
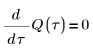
3. 시간 0에서 전하 Q를 정의합니다.
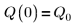
4. 다음과 같은 입력 매개변수 값을 가정합니다.
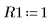
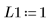
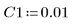
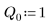
5. 미분 방정식을 표준 형식으로 변환합니다.
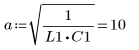
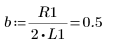
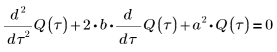
6. a 및 b의 모든 경우에 대해 방정식을 풀이합니다.
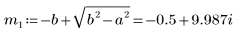
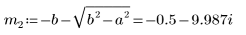
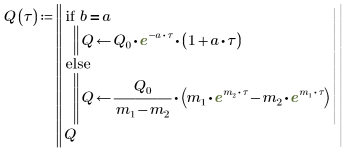
7. Q의 가능한 두 해를 도표화합니다.
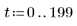
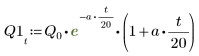
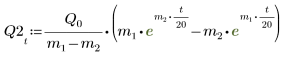
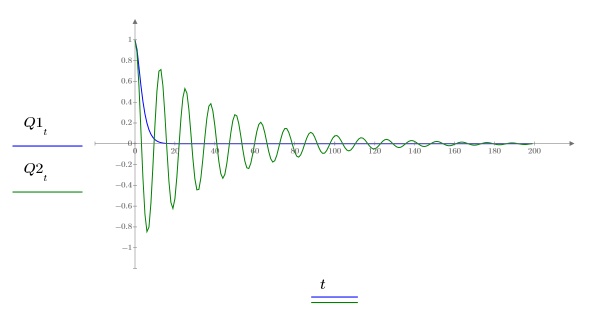
전하 Q1는 a=b인 경우 빠르게 0으로 감쇠되고 a와 b가 같지 않은 경우 0으로 감쇠될 때까지 긴 시간 동안 진동합니다.
ODE 풀이 시스템 사용 전
• ODE 풀이 시스템 함수로 전달할 매개변수를 정의합니다.
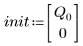 | 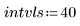 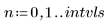 |
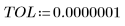 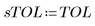 | 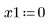 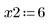 |
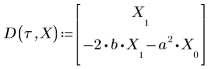 |
• ODE 풀이 시스템은 가파른 시스템 풀이와 가파르지 않은 시스템 풀이의 두 가지 형식으로 구분됩니다. y' = Ax처럼 행렬 형식으로 작성된 ODE 시스템에서 A가 근접 특이 행렬인 경우에는 가파른 시스템이라고 하며, 그렇지 않은 경우에는 가파르지 않은 시스템이라고 합니다.
• 가파른 시스템과 가파르지 않은 시스템 간의 구분은 행렬 A의 고유값에 의해 특성화되는 고유 동적 배율과 연관시킬 수 있습니다. 서로 많이 다른 고유값(아주 작은 값에서 아주 큰 값까지의 범위에 속하는 값)으로 구성된 행렬은 대개 가파른 시스템입니다.
• 지정된 시스템 매개변수를 기반하는 이 간단한 감쇄 조화 예제에서는 가파르지 않은 시스템을 보여줍니다.
가파르지 않은 시스템의 ODE 풀이 시스템 사용
가파르지 않은 시스템에 대한 ODE 풀이 시스템을 사용하여 근사해를 찾은 후 결과를 Q의 정확한 해와 비교합니다.
1. Adams
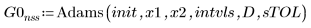
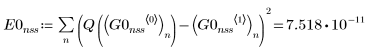
2. rkfixed
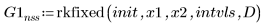
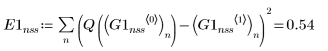
3. Rkadapt
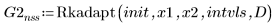
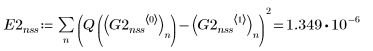
4. Bulstoer
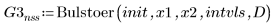
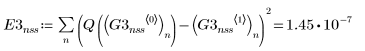
가파른 시스템의 ODE 풀이 시스템 사용
가파른 시스템에 대한 ODE 풀이 시스템을 사용하여 근사해를 찾은 후 결과를 Q의 정확한 해와 비교합니다.
1. BDF
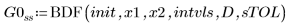
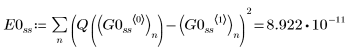
2. Radau
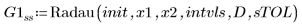
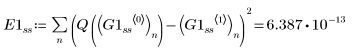
ODE 복합형 풀이 시스템 사용
시스템이 가파른지 여부를 확인하여 그에 따라 Adams 또는 BDF를 호출하는 ODE 복합형 풀이 시스템인 AdamsBDF를 사용하여 근사해를 찾은 후 결과를 Q의 정확한 해와 비교합니다.
1. AdamsBDF
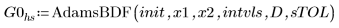
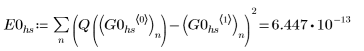
결론
• 가파르지 않은 시스템에 대한 ODE 풀이 시스템 내에서 함수 Adams 및 rkfixed는 각각 최소 오차와 최대 오차의 해를 구합니다.
• 가파른 시스템에 대한 ODE 풀이 시스템 내에서 함수 Radau 및 BDF는 각각 오차가 더 작아지는 해와 오차가 더 커지는 해를 구합니다.
• 복합형 함수인 AdamsBDF는 Adams 또는 BDF로 구한 값보다 더 작은 값을 구합니다.
• 종합적으로, 함수 Radau 및 rkfixed는 각각 최소 오차와 최대 오차의 해를 구합니다.
결과 비교
1. 가파르지 않은 시스템에 대해 ODE 풀이 시스템이 구한 최소 오차(Adams, G0nss) 및 최대 오차(rkfixed, G1nss)의 해를 도표화합니다.
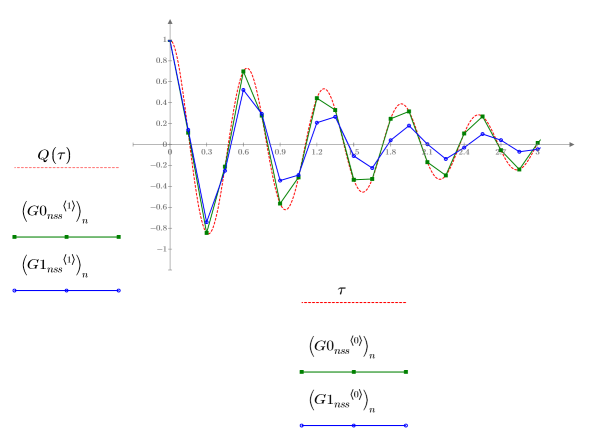
Q와 비교할 경우 이렇게 구한 두 해 간에는 큰 차이점이 있습니다.
2. 가파른 시스템에 대해 ODE 풀이 시스템이 구한 최소 오차(Radau, G1ss) 및 최대 오차(BDF, G0ss)의 해를 도표화합니다.
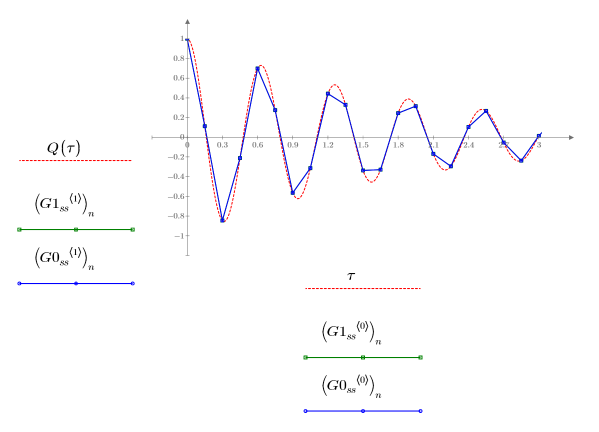
두 해는 Q에 대해 동일하게 나타납니다.
3. 가파른 시스템과 가파르지 않은 시스템에 대해 ODE 풀이 시스템이 구한 최소 오차(Radau, G1ss) 및 최대 오차(rkfixed, G1nss)의 해를 도표화합니다.
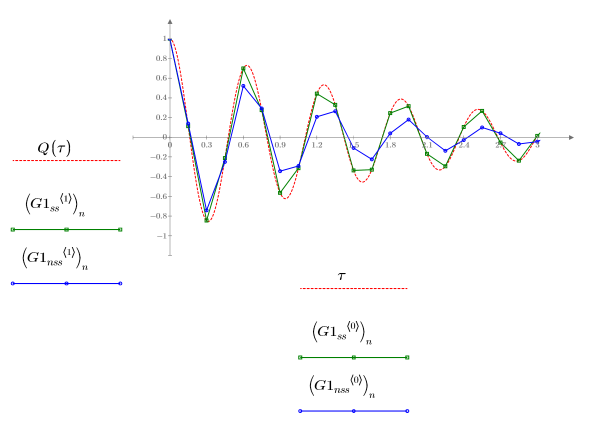
가파른 시스템의 풀이 시스템인 함수 Radau는 Q에 대한 최상의 근사해를 구합니다.