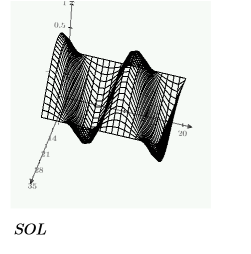
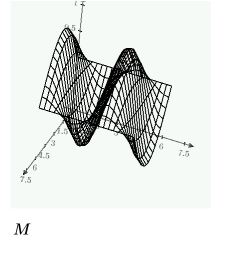
예제: 풀이 구간의 PDE
풀이 구간의 PDE(편미분 방정식)와 편미분 방정식 해결자 numol을 사용하여 파동 방정식의 해를 비교합니다.
PDE 풀이 구간
다음 1차원 파동 방정식을 풀기 위해 다음을 수행합니다.
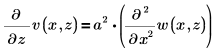
제약 조건을 사용합니다.
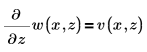
첫 번째 방정식을 두 편미분 방정식으로 이루어진 시스템으로 캐스트하기 위해 PDE 풀이 구간을 설정합니다.
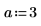
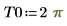
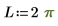
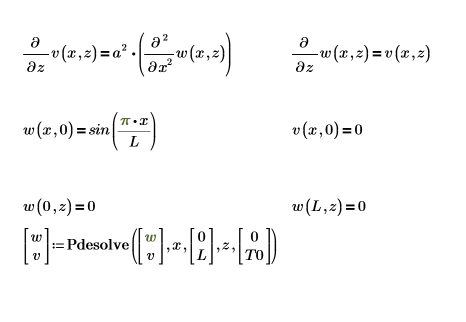
이 경계의 단일 해는 다음과 같습니다.
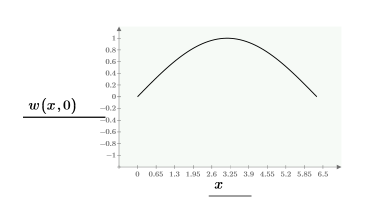
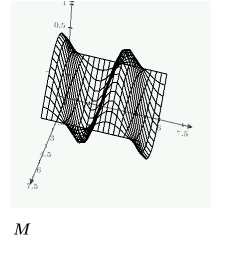
위에서 정의한 제약 조건과 CreateMesh 함수를 사용하여 3차원으로 도표화할 해의 격자선을 만듭니다.
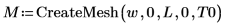
numol 사용하기
명령줄 해결자 numol을 풀 수 있습니다. 이 방법은 계산을 프로그램에 포함하려는 경우에 특히 유용합니다.
시스템에서 편미분 방정식 및 대수 제약 조건의 수를 정의합니다.
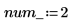
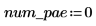
PDE의 우변을 계산하는 함수는 길이 num_pde+num_pae의 벡터입니다(편대수 방정식). 이 경우 함수는 방정식 시스템입니다. 마찬가지로 경계 조건은 길이 num_pde+num_pae의 열 벡터로 정의됩니다.
PDE 벡터에 대한 식은 다음과 같습니다.
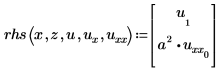
즉 위에서 정의한 바와 같이 u1=v이고 u0=w입니다.
초기 조건 벡터:
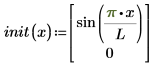
각 좌변이 알 수 없는 함수 벡터 u의 1차 시간 도함수라고 가정합니다. 이 함수의 변수는 x(공간)와 t(시간)입니다. 해는 u이며, 방정식 시스템 해의 벡터도 될 수 있습니다(각 해 u의 1차 도함수인 ux 및 2차 공간 도함수인 uxx).
u, ux, uxx의 개별 항목을 다룰 때는 벡터 아래 첨자를 사용해야 합니다.
경계 조건의 벡터에는 세 가지 유형의 행이 있을 수 있습니다. 각 행은 다음 중 하나에 의해 결정됩니다.
• rhs는 2차 공간 도함수를 포함합니다. 적분 영역의 양면에 각각 하나씩 두 경계 조건(디리클레 "D" 또는 노이만 "N")이 필요합니다.
• rhs는 1차 공간 도함수를 포함합니다. 적분 영역의 왼쪽 또는 오른쪽에 디리클레 경계 조건 하나가 적용되며, 반대쪽은 "NA"입니다.
• 벡터에 공간 도함수가 없는 경우 경계 조건이 필요하지 않습니다.
왼쪽과 오른쪽 경계의 경계 조건은 다음 규약을 따릅니다.
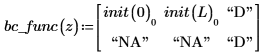
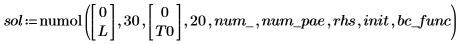
numol의 결과는 공간 상의 각 점을 행으로, 시간 상의 각 점을 열로 나타내는 행렬입니다. 이는 한 번에 한 열을 선택하여 단일 시간점의 모든 공간에 대한 해를 나타낼 수 있도록 함으로써 해의 시각화를 용이하게 합니다. 방정식 시스템을 풀 때 알 수 없는 함수 각각에 대한 해 행렬이 이전 행렬의 측면에 추가됩니다.
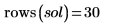
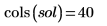
현재 예제의 경우 각 함수에 대해 시간점이 20개이므로 행렬에 40열이 포함됩니다. 첫 번째 해 u0을 선택합니다.
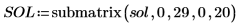
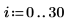
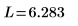
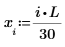
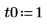
numol과 Pdesolve 비교
t0 점에서 numol과 Pdesolve를 비교합니다.
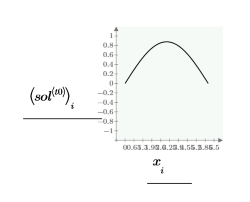
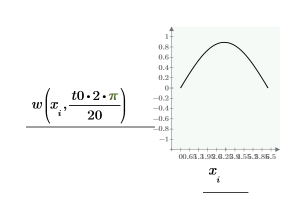
공간 및 시간 값에 대한 해의 격자선을 비교합니다.