非線形回帰
genfit(vx, vy, vg, F) - x の関数 F と n 個のパラメータ u1... un を vx と vy のデータに最も近似させるパラメータを持つベクトルを返します。
genfit 関数は、Levenberg-Marquardt 法の最適化されたバージョンを最小化に使用します。この実装では通常、計算が高速化され、推定値の精度が低い場合にも大きな影響はありませんが、有理関数などでは極小値が多くなるため、うまく収束しない場合があります。この実装は間違った微分ベクトルの影響を受けます。
引数
• vx, vy は、データセット内の x 値と y 値に対応する、同じ長さの実数データ値のベクトルです。データ点の数はパラメータの数以上にする必要があります。
• vg はパラメータの推定値の n 要素のベクトルです。n = 1 の場合、vg はスカラーです。
• F(x, u) は適合関数または関数のベクトルです。ここで、x は独立変数、u はパラメータのベクトルまたは個々のパラメータ名です。次の式は、適合関数の有効な表現です。
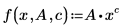
• n は正の整数です。パラメータがベクトル化されていない場合、使用できる個別の名前は 9 個までです。
収束の改善
収束を改善し、genfit の精度を向上させるには、F を関数の n+1 ベクトルとして表すことができます。ここで、最初のエントリ F0 は適合関数 f で、その他のエントリ F1、F2、...、Fn は n パラメータに関する f のシンボリックな偏微分です。
上記の 2 つの方法で適合関数を表す場合、シンボリックに偏微分を検索する際は、f(x,A,c) のみを使用できます。F を関数のベクトルとして表す際は、n の限度は 9 となり、F の最大長さは 10 となります。適切な偏微分の行列を構築し、これをシンボリックに評価することで、ベクトル F を作成できます。
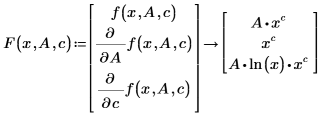
追加情報
• genfit には、適合関数または関数のベクトルの名前だけを指定し、引数は指定しません。
• シンボリックなパラメータの偏微分を使用せずに、適合関数を使用する場合、genfit によってパラメータの偏微分が数値的に計算されます。この場合、シンボリックな微分よりも精度が下がりますが、状況によっては便利です。
• genfit が変換に失敗した場合は、代替の「Levenberg-Marquardt」法、別の推定値を使用するか、すべてのパラメータが同程度の大きさになるようにデータをスケーリングできます。
• 「最適化 Levenberg Marquardt」求解アルゴリズムは、与えられた代数的微分の誤差の影響をより強く受けます。この方法が失敗した場合は、微分の式を確認します。
• すべての数値解決法と同様に、非線形問題は推定値に大きく左右されます。推定値のある適合関数をプロットできます。これは、genfit を使用する前に推定値を微調整するために役立ちます。