例: 確率分布

関数 > 統計 > 確率分布 > 例: 確率分布

例: 確率分布

確率分布表の代わりに確率分布関数を使用します。

確率密度

1. dchisq関数を使用して、自由度 11 のχ二乗変数が 5.5 のときの確率密度を計算します。

2. dt関数を使用して、自由度 4 の変数 t が -1.56 のときの確率密度を計算します。

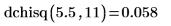
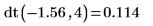
累積確率

1. pnorm関数を使用して標準正規変数が 1.0 を超える確率を計算します。

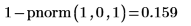
2. pchisq関数を使用して、自由度 7 のχ二乗変数が 5.6 未満である確率を計算します。

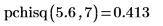
3. pbinom関数を使用して、大きさ 15、パラメータ 0.6 の二項変数が 10 以下である確率を計算します。

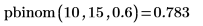
4. qbinom関数を使用して、大きさ 15、パラメータ 0.6 の二項変数が 10 以下である確率を計算します。

5. rbinom関数を使用して、サイズ n=7 の二項分布に従い、成功の確率が q=0.65 の m=5 乱数のベクトルを作成します。

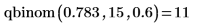
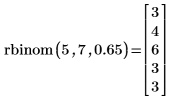
ワークシートを再計算すると、関数 rbinom により一連の乱数が新しく返ります。

6. dbeta関数を使用して、実数形状パラメータが 3 と 2 の値 x=0.8 の確率密度を計算します。

7. pbeta関数を使用して、a=3 および b=2 のベータ変数が 0.8 を超える確率を計算します。

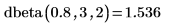
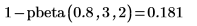
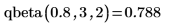
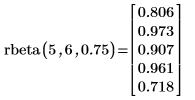
8. 関数qbetaを使用して確率 p=0.8 の逆累積確率分布を計算します。

9. rbeta関数を使用して、サイズ n=6 の二項分布に従い、成功の確率が q=0.75 の m=5 乱数のベクトルを作成します。

逆累積確率

1. 関数qnormを使用して確率 p の逆累積確率分布を計算します。

2. 関数qtを使用して確率 p の逆累積確率分布を計算します。

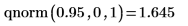
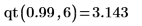
F 分布

1. dF関数を使用して、自由度 4 および 6 の F 分布の 65 番目のパーセンタイルを計算します。

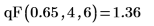
2. pF関数を使用して、自由度 5 および 7 の確率 0.75 の累積確率分布を計算します。

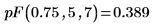
3. qF関数を使用して、自由度 9 および 8 の F 分布の 95 番目のパーセンタイルを計算します。

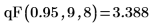
4. rF関数を使用して、F 分布に従い、自由度が 2 および 3 の 7 乱数のベクトルを作成します。

ワークシートを再計算すると、関数 rF により一連の乱数が新しく返ります。