例: 解のパラメータ化
root関数またはソルブブロックによって、不明なパラメータに依存した方程式または連立方程式を解く関数を定義します。これによって一連の連立方程式全体を解くことができます。
root 関数
パラメータ a の値を変えて方程式 f1=f2 を解きます。
1. 2 つの関数を定義します。
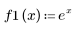
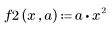
2. 新しい関数 S を定義し、a の値を変えて方程式を解きます。
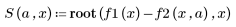
3. 初期推定値を定義します。
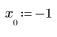
4. パラメータ a の範囲を定義し、その範囲内でパラメータの値を変えて方程式を解きます。
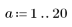
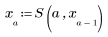
 |  | 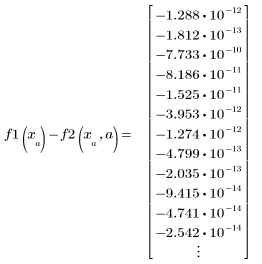 |
ソルブブロック: 摩擦係数
e の値 (パイプの粗さ)、D (パイプの直径)、R (レイノルズ数) が与えられたときの摩擦係数 f を求めます。
1. 推定値を定義します。
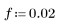
2. 摩擦係数を計算する関数を定義するソルブブロックを記述します。

パラメータ e、D、R はまだ定義されていません。関数 FricFac を計算する場合は、これらのパラメータに新しい値を指定して、ソルブブロックを再び呼び出すことができます。
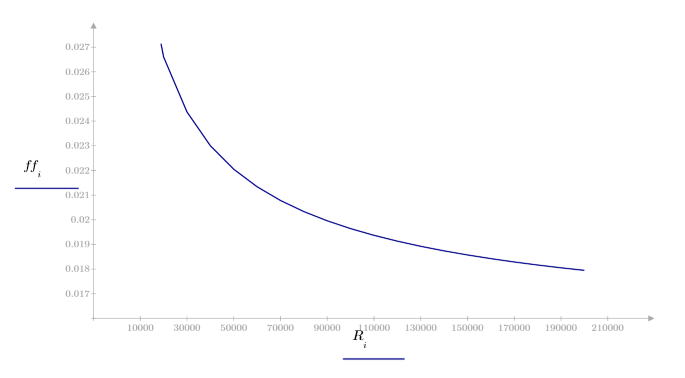
3. レイノルズ数の値を変えて摩擦係数を計算します。
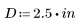
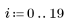
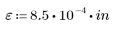
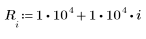
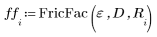
ソルブブロック: 円と直線の交点
1. 円の半径の値を変えて円と直線 y = 2 - x の交点を求めます。
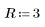
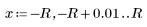
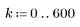
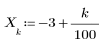
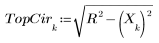
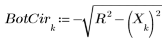
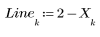
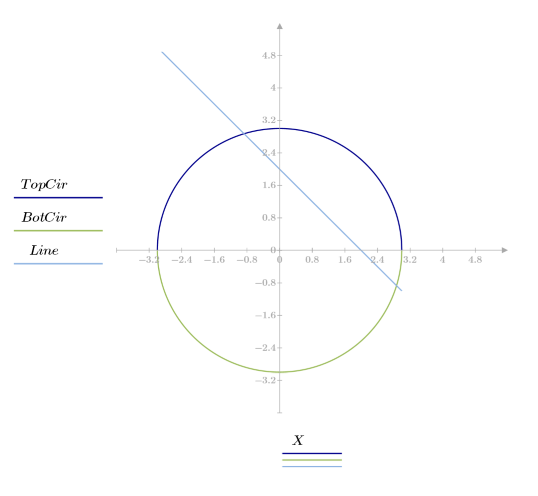
2. 直線 y = 2 - x と半径 R の円との交点の座標を返す関数を定義するソルブブロックを記述します。
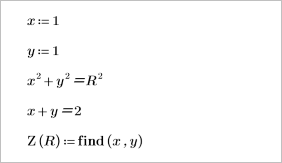
3. 新しく定義した Z 関数を使用して、R=3 で推定値が x=1、y=1 のときの交点の座標を求めます。
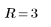
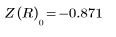
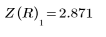
4. 交点をプロットします。
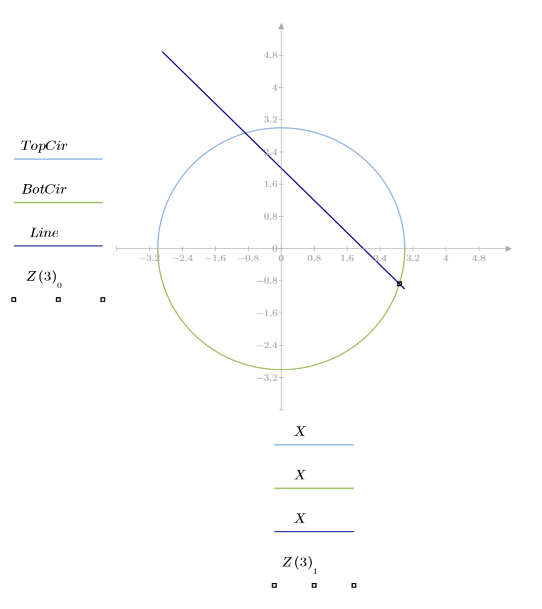
5. 新しく定義した Z 関数を使用して、半径 R を 5 つの異なる値に変えて交点の座標を求めます。
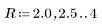
 | 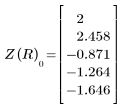 |  |
Z(R, x, y) を定義することで、推定値について上記のソルブブロックをパラメータ化できます。これによって、1 つのソルブブロック設定で各半径に対する 2 つの異なる解を求めることができます。