例: 線形回帰
関数polyfitc、line、slope、およびinterceptを使用して、一連の x-y データについての最良適合の最小二乗直線を求めます。stderr関数を使用して、適合パラメータの誤差を計算します。最良適合の直線の信頼限界を計算して信頼区間を求めます。
最良適合の直線
さまざまな距離のドライブに要する時間を推定する線形関数を作成します。
1. 距離 (マイル) と走行時間 (分) の組み合わせを定義します。
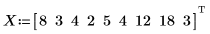
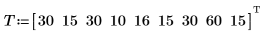
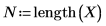
2. 単変量線形回帰方程式を定義します。
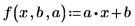
3. polyfitc を呼び出して回帰係数 a と b を計算します。
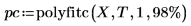
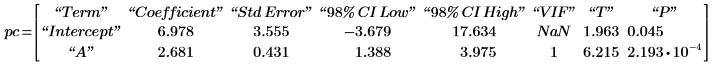

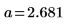
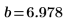
4. 各点からの距離の二乗の和が最小となるような最良適合直線を定義します。
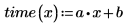
線形またはその他のタイプの回帰のパラメータ方程式は、値が元の観測データに近い場合にのみ使用します。上記のデータについての最良適合の直線では、0 マイルの距離を移動するときにかかる時間が次のように予測されます。
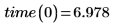
測定時間が一定の速度による厳密な移動時間を表す場合、この予測ではつじつまが合いません。この種の結果によってなんらかの物理現象が表されることがあります。この場合、0 マイルを走行するのに要する時間は、信号待ちの平均時間と見なすことができます。
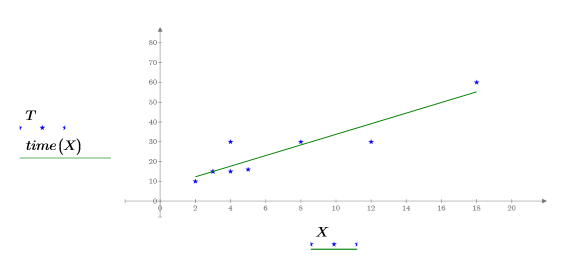
5. データ点および最良適合の直線をプロットします。
傾きと切片のその他の計算方法
最良適合の直線の傾きと切片を計算するにはいくつかの方法があります。たとえば、line 関数は slope 関数と intercept 関数が組み合わさったものです。行列計算や統計関係を利用する方法もあります。
1. intercept 関数と slope 関数を呼び出します。
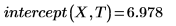
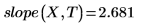
2. line 関数を呼び出します。
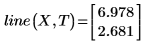
3. augment関数を使用して行列計算を行います。
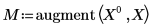
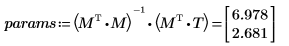
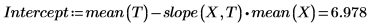
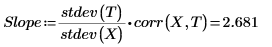
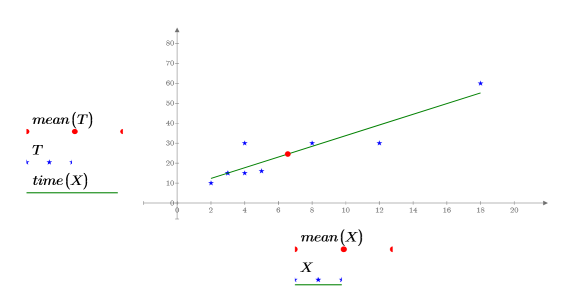
5. プロットを使用して最小二乗直線が常に点 (mean(X), mean(T)) を通ることを示します。
標準誤差
推定値の標準誤差 (単に標準誤差とも呼ぶ) を計算し、上記の線形適合がどの程度良好であるかを測定します。傾きと切片の誤差も計算します。
1. 自由度 (データ点の数から適合パラメータの数を引いた値) を定義します。
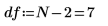
2. stderr 関数を呼び出して、上記で定義した最良適合の直線の推定値の標準誤差を計算します。
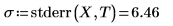
これは二乗平均誤差 (MSE または σ2) の平方根となります。
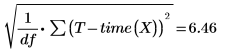
3. 計算した標準誤差とpolyfitstat関数で返された標準誤差を比較します。
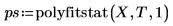
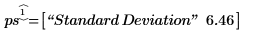
4. 傾きと切片の標準誤差を計算します。
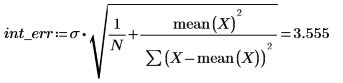
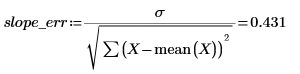
5. 行列計算を使用して前述の計算を繰り返します。
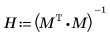
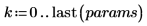
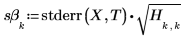
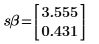
6. augment 関数を使用して、各回帰係数の標準誤差が polyfitc 関数によって返る行列に記録されることを示します。
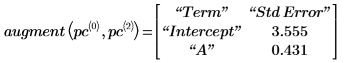
各係数の信頼区間
上記の推定値をスチューデントの t 分布の四分位点とともに使用して、傾きと切片の推定値の信頼区間を求めます。
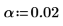
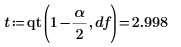
2. 傾きの信頼限界を計算します。
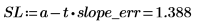
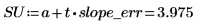
傾きの実際の値が SL から SU までの範囲内になる可能性は 98% です。
3. 切片の信頼限界を計算します。
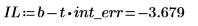
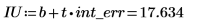
この値の範囲が広いことから、データが広範に分散していることがわかります。
4. confidence関数を呼び出して手順 1 から 3 を繰り返します。
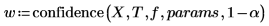
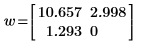
confidence 関数は、1 列目に信頼区間の幅を返し、2 列目に係数 t の値を返します。幅を係数 t で割ると、両方のパラメータの標準誤差になります。
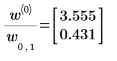
5. 信頼限界を求めるには、関連するパラメータに幅を加算するかパラメータから幅を減算します。
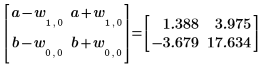
6. augment 関数を使用して、各回帰係数の標準誤差が polyfitc 関数によって返る行列に記録されることを示します。

回帰の信頼区間
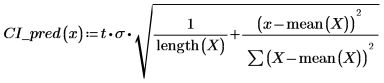
2. 前述の関数を使用して予測される任意の x 値の信頼区間を計算します。
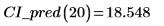
3. 行列計算を使用すると次のような結果になります。
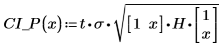
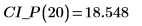
4. データ、最良適合の直線、および回帰領域全体における信頼区間をプロットします。
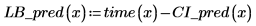
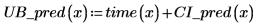
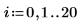
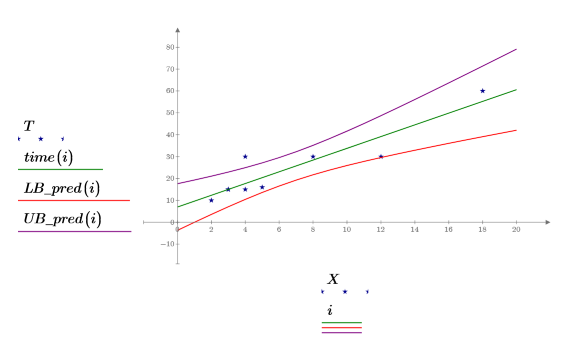
予測値の信頼領域では測定値の中央付近にくびれがあります。これは、回帰の計算に使用した公式が平均値に基づいているので、データの平均に近いほど予測値の精度が高くなるためです。
5. 測定値の信頼限界を計算します。測定値の信頼限界は予測値の信頼限界とは若干異なります。
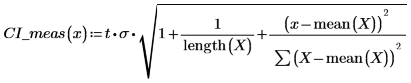
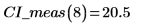
6. 行列計算を使用すると次のような結果になります。
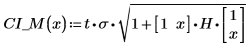
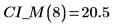
7. 信頼限界を誤差トレースとしてプロットします。
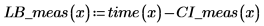
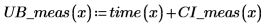
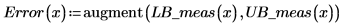
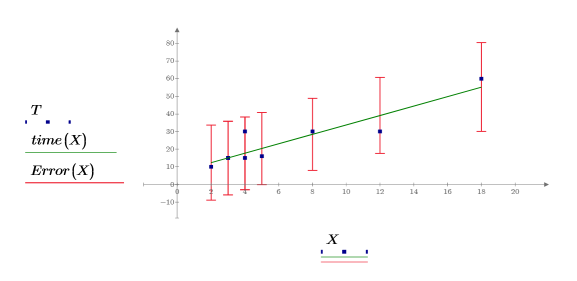
信頼区間の外にある測定値は外れ値となるので、外れ値を検出する手段としてグラフを利用できます。 |