例: 正方形プレートの熱流量

関数 > 求解と最適化 > 微分方程式ソルバー > 例: 正方形プレートの熱流量 - II

例: 正方形プレートの熱流量 - II

偏微分方程式ソルバーrelaxを使用して正方形プレートの定常状態における温度分布を求めます。

ポアソンの方程式の求解

source 関数の値が既知であり、境界条件がゼロでない熱方程式を解きます。

relax 関数はまったく異なる求解方法に基づいており、したがって異なる引数の一式を必要とします。

1. 5 つの正方行列 a、b、c、d、および e を定義して、ラプラス近似の係数を含めます。

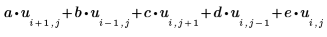
これらの配列のサイズは任意に指定できます。大きいほど解におけるメッシュは細かくなります。

2. 正方形プレートの寸法を定義します。

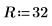
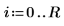
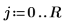
3. 係数を次のように定義します。

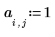
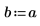
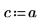
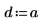
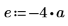
4. 一定熱源の強さと位置を定義します。

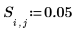
5. グリッドのサイズと等しいサイズの正方行列 f を定義して、関数 F(x,y) の既知の境界値と未知の内部値の推定値を含めます。

◦ 最上面の境界条件は次のとおりです。

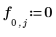
◦ 底面の境界条件は次のとおりです。

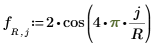
◦ 端の境界条件は次のとおりです。

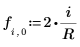
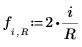
6. 0 から 1 までの実数である Jacobi spectral radius 変数 r を定義します。

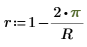
このパラメータは緩和アルゴリズムの収束を制御します。"反復計算が多すぎます" というエラーメッセージが表示された場合は、r を小さくしてみてください。

7. relax 関数を次のように呼び出します。

<region id="ID0E2L25" top="1516.8000000000002" left="38.400000000000006" height="25.6" width="204.10333333333335" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">F</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">relax</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">c</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">e</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">f</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">r</id>
        </sequence>
      </apply>
    </define>
  </math>
</region>

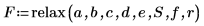
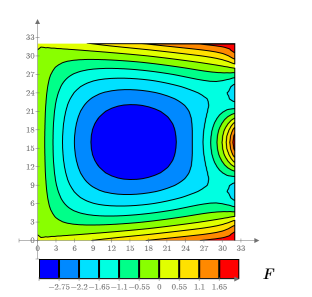
8. 3D プロットを作成して、正方形プレートの熱分布を示します。

<region id="ID0ELN25" top="1747.2000000000003" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="32" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-3" end="4.5">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">F</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.052623873051966662</Cell>
          <Cell>0.043294250885890617</Cell>
          <Cell>0.99767546618388891</Cell>
          <Cell>0</Cell>
          <Cell>0.095704097834471175</Cell>
          <Cell>0.99467978821191028</Cell>
          <Cell>-0.038116198399097093</Cell>
          <Cell>0</Cell>
          <Cell>-0.99401783366431629</Cell>
          <Cell>0.093475808436936883</Cell>
          <Cell>-0.056487340124674094</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>直交</CameraType>
    </plot3D>
  </plot>
</region>

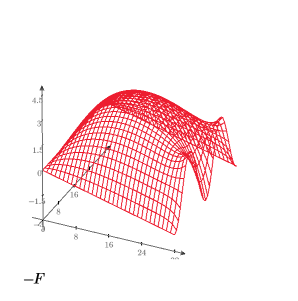
9. 等高線図を作成して等温線を表示します。