例: 幾何分布関数と超幾何分布関数

関数 > 統計 > 確率分布 > 例: 幾何分布関数と超幾何分布関数

例: 幾何分布関数と超幾何分布関数

幾何分布

1. 関数dgeomを使用して値 k の確率密度を計算します。

2. 関数pgeomを使用して値 k の累積確率分布を計算します。

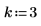
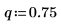
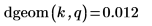
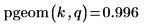
3. 関数 pgeom を使用して確率 p の逆累積確率分布を次のように計算します。

4. 関数rgeomを使用して、幾何分布に従う m 乱数のベクトルを次のように作成します。

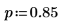
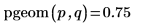
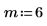
ワークシートを再計算すると、関数 rgeom により一連の乱数が新しく返ります。

超幾何分布

1. 入力パラメータ a、b、m、n を定義します。パラメータは、

max{0, n − b} ≤ m ≤ min{n, a} かつその他の m では 0 という関係を満たす整数です。

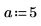
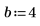
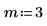
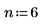
2. 関数dhypergeomを使用して超幾何分布の確率密度を次のように計算します。

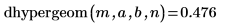
3. 関数phypergeomを使用して累積確率分布を次のように計算します。

4. 関数qhypergeomを使用して確率 p の逆累積確率分布を計算します。

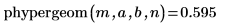
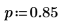
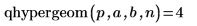
5. 関数rhypergeomを使用して、超幾何分布に従う m 乱数のベクトルを次のように作成します。

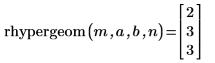
ワークシートを再計算すると、関数 rhypergeom により一連の乱数が新しく返ります。