例: 回路内の減衰調和運動
抵抗 R、コイル L、コンデンサ C から成る単純な電気回路があるとします。
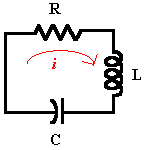
微分方程式を使用してコンデンサ C における電荷 Q をモデル化してから、ODE ソルバー関数を使用してその他の近似解を求めます。最後に、その結果を Q の厳密解と比較します。
微分方程式の使用
1. この 3 つのコンポーネント間の電圧を表す微分方程式を記述します。電圧の合計はゼロでなければなりません。
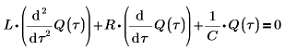
2. コンデンサ C における電荷 Q の瞬間的変化を表す微分方程式を記述します。
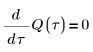
3. 時刻ゼロにおける電荷 Q を定義します。
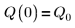
4. 入力パラメータとして次の値を使用します。
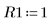
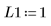
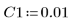
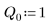
5. 微分方程式を標準形式に変換します。
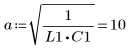
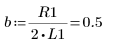
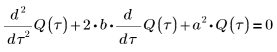
6. a と b のあらゆるケースで方程式を解きます。
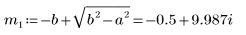
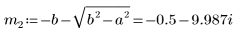
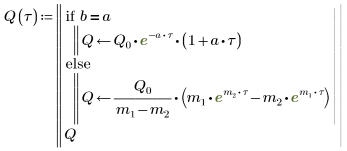
7. Q のとりうる 2 つの解をプロットします。
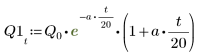
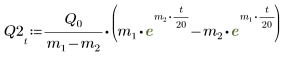
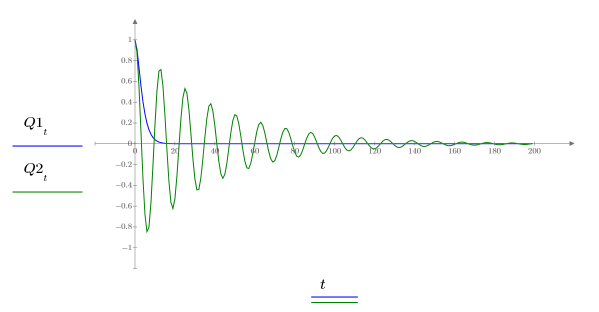
a=b の場合、電荷 Q1 はただちにゼロに減衰し、a と b が等しくない場合には長時間振動してからゼロになります。
ODE ソルバを使用する前に
• ODE ソルバ関数に渡されるパラメータを定義します。
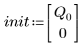 |  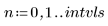 |
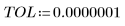 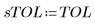 | 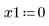 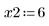 |
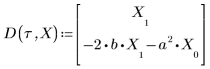 |
• ODE ソルバは、スティフな連立方程式を解くためのソルバと、スティフでない連立方程式を解くためのソルバの 2 種類に区別されます。y' = Ax という行列形式で記述された連立常微分方程式で、行列 A がほぼ特異な場合、その連立方程式はスティフです。そうでない場合、その連立方程式はスティフではありません。
• 連立方程式がスティフであるかどうかは、行列 A の固有値として表れる行列 A 固有の力学的スケールに関連します。固有値がばらばらな (非常に小さな値から非常に大きい値までを含む) 行列は、通常はスティフな連立方程式です。
• 指定された連立方程式のパラメータによると、この単純な減衰調和の例はスティフでない連立方程式です。
スティフでない連立方程式用の ODE ソルバの使用
スティフでない連立方程式用の ODE ソルバを使用して近似解を求めてから、その結果と Q の厳密解を比較します。
1. Adams
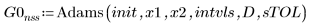
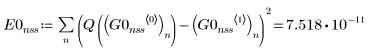
2. rkfixed
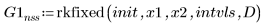
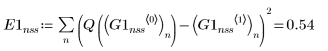
3. Rkadapt
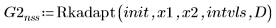
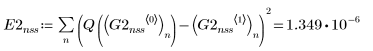
4. Bulstoer
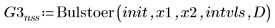
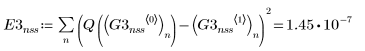
スティフな連立方程式用の ODE ソルバの使用
スティフな連立方程式用の ODE ソルバを使用して近似解を求めてから、その結果と Q の厳密解を比較します。
1. BDF
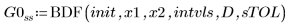
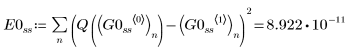
2. Radau
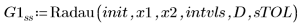
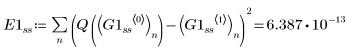
ODE ハイブリッドソルバの使用
連立方程式がスティフかスティフでないかを判別して結果に応じて Adams または BDF を呼び出す ODE ハイブリッドソルバ AdamsBDF を使用し、Q の近似解を求めてから、その結果と厳密解を比較します。
1. AdamsBDF
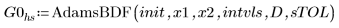
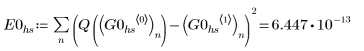
結論
• スティフでない連立方程式用の ODE ソルバ内で、関数 Adams は誤差が最小となる解を返し、関数 rkfixed は誤差が最大となる解を返します。
• スティフな連立方程式用の ODE ソルバ内で、関数 Radau は誤差がより小さい解を返し、関数 BDF は誤差がより大きい解を返します。
• ハイブリッド関数 AdamsBDF は、Adams または BDF によって返る値よりも誤差が小さい値を返します。
• まとめると、関数 Radau は誤差が最小となる解を返し、関数 rkfixed は誤差が最大となる解を返します。
結果の比較
1. スティフでない連立方程式用の ODE ソルバから返った、誤差が最小の解 (Adams, G0nss) と最大の解 (rkfixed, G1nss) をプロットします。
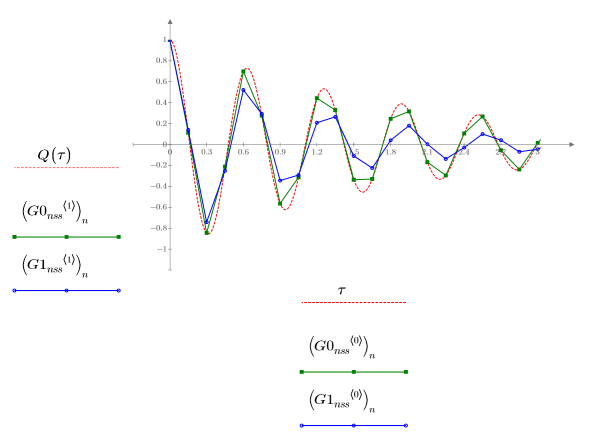
Q と比較すると、返された 2 つの解には明らかな違いがあります。
2. スティフな連立方程式用の ODE ソルバから返った、誤差が最小の解 (Radau, G1ss) と最大の解 (BDF, G0ss) をプロットします。
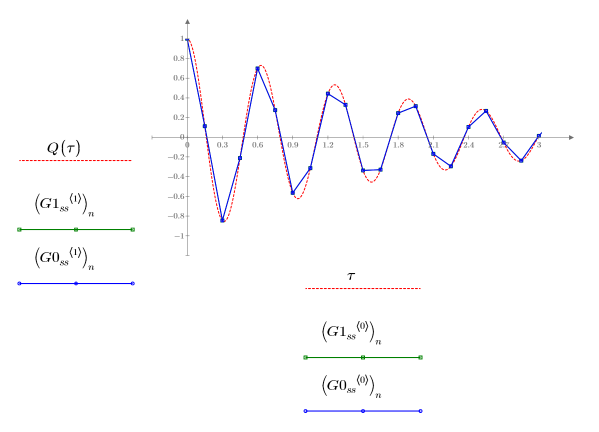
この 2 つの解は Q に関してはまったく同じに見えます。
3. スティフな連立方程式用の ODE ソルバとスティフでない連立方程式用の ODE ソルバから返った、誤差が最小の解 (Radau, G1ss) と最大の解 (rkfixed, G1nss) をプロットします。
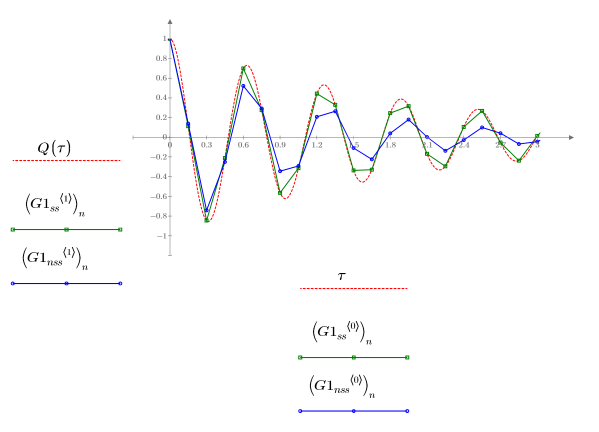
スティフな連立方程式用のソルバである関数 Radau は、Q の解の最適近似を返します。