例: レプリケートを持たない因子計画の ANOVA
anova関数は、レプリケートを持つ因子計画で分散分析を行う関数です。レプリケートを持たない計画の場合は、有意でない因子を見つけ出し、除去し、計画の次元を下げ、結果をレプリケートしておきます。
1. fullfact関数を呼び出して、パイロットプラントの濾過速度をテストする実験の全因子計画行列を作成します。因子 A、B、C、D は、それぞれ温度、圧力、ホルムアルデヒト濃度、攪拌速度を表します。
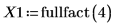
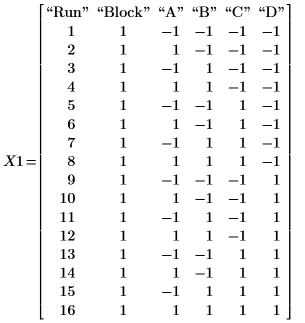
2. 16 回ごとにひとつの要素で、実験の結果を行列 Y1 に記録します。

3. quickscreen関数を呼び出して、各主因子の平均応答を取得します。

4. 効果グラフを作成して、有意因子を判断します。
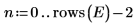
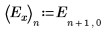
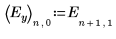
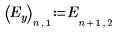

因子 C と C に関連する 2 次交互作用は実験にあまり影響がありません。因子 A、B、D と比べて、因子 C は有意ではありません。
5. anova 関数を呼び出して分散分析を行います。
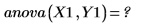
Y1 はレプリケートされていないので、anova 関数はエラーを返します。ただし、C は有意でないので、因子 A、B、D について見ると、“Run 1” と "Run 5" で重複しています。これは “Run 2" と "Run 6" にも当てはまります。実際には、C が有意でない場合、元の ABCD 24 の計画行列には ABD 23 の計画行列が重複して格納されます。
6. fullfact 関数を呼び出して、23 の全因子計画行列を作成します。

X2 では因子名が変わっています。A、B、D であった因子が A、B、C になります。
7. 実験結果を 23 の全因子実験に合わせて配列し直します。
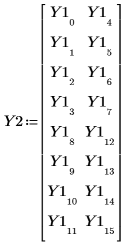
8. Y2 を使用して、anova 関数を呼び出します。
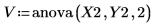
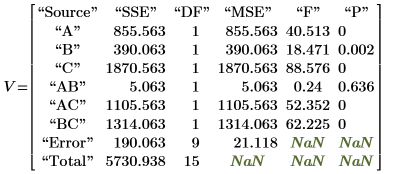
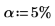
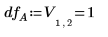
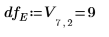
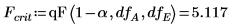
◦ 効果プロットから、A、B、D と比べて、因子 C は有意ではないと判断できます。
◦ 因子 A、B、D (V では A、B、C) および交互作用 AD、BD (V では AC、BC) は、それらの F-values が Fcrit を上回っているので、5% のレベルで有意です。この分散分析によって、効果グラフから導かれた主観的な結論が裏付けされました。
参考文献
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 246.