例: 1 因子 ANOVA
1. 新しい合成繊維の強度に対する綿花の量の影響をテストする実験での因子の数を定義します。
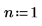
2. 実験で使用する綿花の設定を行います。
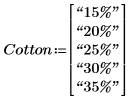
3. 関数lengthを使用して因子のレベルの数を定義します。
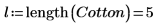
4. 関数 fullfact を呼び出して、実験とそのランを表す全因子計画行列を作成します。
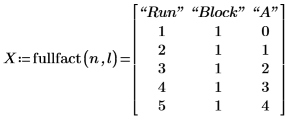
計画行列 X で、A は綿花の因子を表し、その水準は次のように符号化されています。
A の符号化された値 | A の実際の値 |
|---|---|
0 | 15% |
1 | 20% |
2 | 25% |
3 | 30% |
4 | 35% |
5. 綿花の重量が 15% の場合の 1 つ目のランでの合成繊維の強度を測定します。
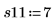
6. 残り 4 つのランでの測定を行います。
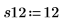
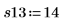
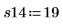
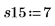
7. 関数randomizeを呼び出してランの順序を入れ替えます。
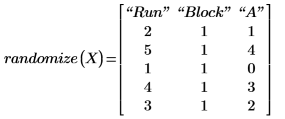
8. randomize 関数によって決まった順序で測定をレプリケートします。
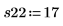
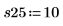
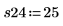
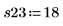
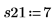
実験を反復することで、制御されていない変数の影響を平均化することができます。実験を反復する前に randomize 関数を呼び出すことで、入力因子間に存在しうる相関関係の影響を抑えることができます。
9. 必要なレプリケートの回数だけ手順 7 と 8 を繰り返します。行列 Y にすべての測定値を格納します。

列によってどのレプリケートのデータであるかを識別し、行によってどのランのデータであるかを識別します。
10. 関数boxplotを呼び出して、各ランが 1 つの箱で表される箱髭図を作成するためのデータを準備します。
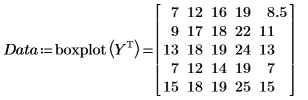
各ランの結果が行列の行に格納されていますが、boxplot に渡すデータは行列の列に格納されている必要があるので、行列 Y が転置されています。
11. 関数boxplotgraphを呼び出します。
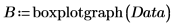
12. 箱髭図を作成します。
a. boxplotgraph 関数の出力を次のようにプロットします。
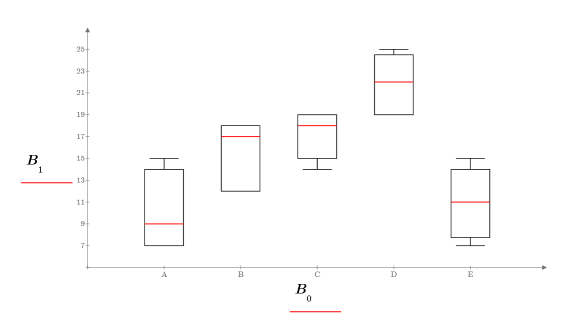
b. 各因子にラベルを付けた次のようなテキスト領域を作成します。
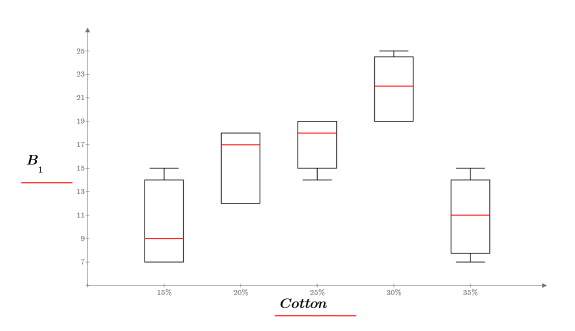
箱髭図から、綿花の重量の割合が繊維の引張り強度に影響を与えていることがわかります。綿花の重量が繊維の重量の約 30% のときに、繊維の引張り強度が最大になっています。
13. 関数 anova を呼び出して、綿花の重量の割合が引張り強度に影響を与えているかどうかをテストします。

14. r をランの回数、x をレプリケートの数として定義して、SSE 列で二乗和を計算します。
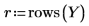
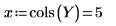
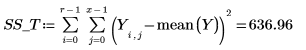
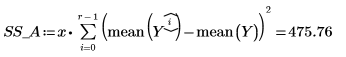
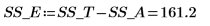
15. N を測定回数の合計と定義して、df 列で自由度を計算します。
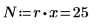
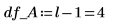
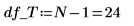
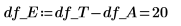
16. MSE 列で二乗平均を計算します。
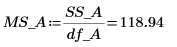
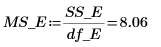
17. 因子 A の F-value を計算します。
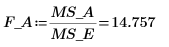
P 列の P-value は 0.05 未満なので、因子 A は有意因子です。
18. F-value を使用して、A が有意因子であるという仮説を検定します。5% の有意水準の F の臨界値を計算します。
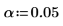
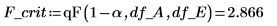
因子 A の F-value は F の臨界値よりも大きいことから、綿花の重量の割合が繊維の引張り強度に影響を与えていることを再確認できます。
参考文献
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001.62.