Partial Differential Equations in Solve Blocks
pdesolve(u, x, xrange, t, trange, [xpts], [tpts]) - Returns a function or vector of functions u(x,t) that solves a one-dimensional nonlinear Partial Differential Equation (PDE) or system of PDEs, with n independent equality constraints for an nth order differential equation. Values are interpolated from a matrix of solution points calculated using the numerical method of lines.
You must use pdesolve in a Solve Block.
Arguments
• u is a scalar function name, or a vector of function name (with no variable names included) as they appear within the solve block. For example, if you are solving for the functions f(x,t) and g(x,t), u would be:
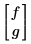
To accommodate the subscript partial differential notation, you cannot use Literal Subscripts when naming functions.
• x is the spatial variable name.
• xrange is a two-element column vector containing the real boundary values for x.
• t is the time variable name.
• trange is a two-element column vector containing the real boundary values for t.
• xpts (optional) is the integer number of spatial discretization points.
• tpts (optional) is the integer number of temporal discretization points.
The general rules of Defining a Solve Block apply. Within the body of the block:
Unknown functions
Functions must be defined in terms of their variables. For example, use u(x,t), not u. To indicate a partial derivative within the solve block, use one of the following:
• Subscript notation. For example, uxx(x,t) is the second partial derivative of u with respect to x.
Subscript notation can be used only in pdesolve in solve blocks, and not in other regions of the worksheet. |
• The partial derivative operator.
PDE Equations
Equations must be defined using Boolean Equals. Second partial derivatives are not allowed on the left-hand-side of equations, you must convert your equation to a system of equations in first derivatives only.
Boundary conditions
There must be an initial condition u(x,0), and n boundary conditions, where n is the order of the PDE, for each unknown function. Mathcad checks for the correct type and number of constraints and flags mistakes with an error message.
• Boundary conditions can be of type Dirichlet (u(0,t) = f(t)), Neumann (ux(0,t)=g(t)), or a mix of the two.
• Boundary conditions can be specified at either endpoint of the spatial integration range. The endpoints used in the boundary conditions must match the endpoints specified in the ode/pdesolve command.
• While Mathcad can solve a pdesolve function with an implicit boundary condition, in some cases the pdesolve function cannot be solved due to limitations of the approximation algorithms. Therefore, it is recommended to use explicit boundary conditions, when possible.
Constraints
Algebraic constraints of the form u(x,t)+v(x,t)+w(x,t)=0 are allowed. This adds an extra unknown function w to the system, which must be specified as one of the output functions in the ode/pdesolve call. Inequality constraints are not allowed.
• Assign the output of the pdesolve function to a function name, or vector of function names.
• To change the approximation method used for the partial derivatives, right-click on the pdesolve function and choose another method. This may affect calculation time.
• The numerical method of lines is only appropriate for solving hyperbolic and parabolic PDEs, and partial algebraic equations. For solving an equation in a program loop, use numol. For solving an elliptic PDE, such as Poisson's equation, use Relax or Multigrid.
Errors and Solution with pdesolve
• Error: This function requires at least 5 arguments but is applied to 4.
Example:
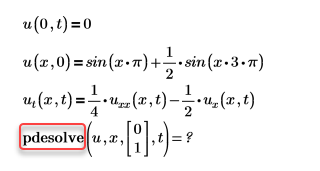
Solution: Add the missing argument, in this case it is trange.
• Error: This function accepts at most 7 arguments but is applied to 8.
Example:
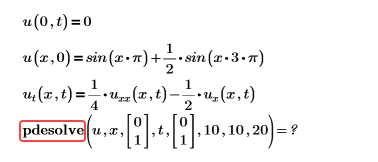
Solution: Remove unnecessary arguments. See more information about Arguments
• Error: Malformed vector of boundaries for time variable.
Example:
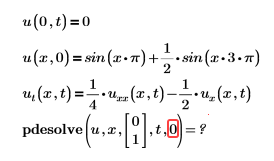
Solution: trange is not defined correctly. See more information in Arguments
• Error: Malformed vector of boundaries for space variable.
Example:
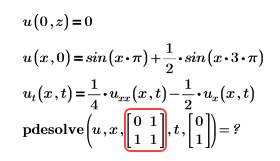
Solution: xrange is not defined correctly. See more information in Arguments
• Error: Unknown function name incorrectly specified.
Example:
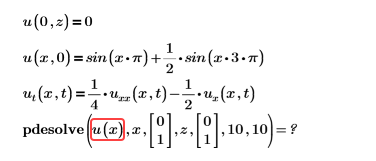
Solution: The function must appear without an argument.
• Error: must be an integer greater than 4.
Example:
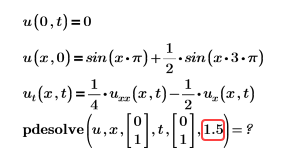
Or
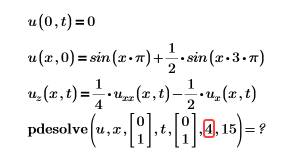
Solution: The number of discretization points must be an integer greater than 4.