Arbortext IsoDraw > User's Reference > Palette Window Toolbox > Transformations > Rotation
  
Rotation
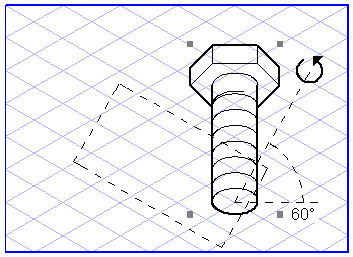
It is possible to rotate all elements in Arbortext IsoDraw. To do this, select the relevant elements with the mouse. Then select the Rotation tool and position the center cursor on the point you want to rotate the selected object around.
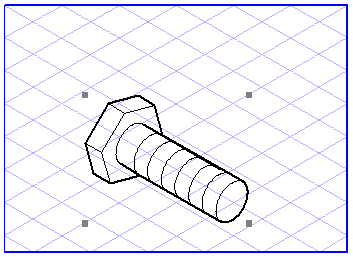
Now drag the cursor over the screen while holding down the mouse button. During this process, the cursor changes to the Rotation cursor. You will also be able to see a line which gives an indication of the rotation angle plus an angle value. A dotted rectangle indicates the orientation the objects will be rotated to. Move the cursor around the rotation point and release the mouse button once you have set the required angle.
* 
The more you move the cursor away from the center of rotation, the more accurately you will be able to specify the angle.
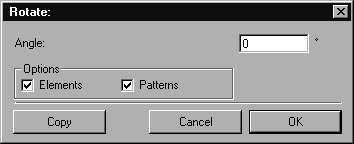
You can also rotate your selection by means of the dialog box. Press the SHIFT key while you specify the rotation point by clicking with the center cursor.
Enter the angle by which you want to rotate the selected object. You can also enter the value as a mathematical formula. You can use this entry option to assist you if, for example, you are looking for the distance required to ensure a uniform distribution of holes around the circumference or for the teeth of a gear wheel. Information on how to enter values can be found in the Drawing Basics Tutorial.
Example:
If you want to determine the angle of rotation for a circle of 8 holes, enter the formula "360/8".
Under Options you can select Elements and Patterns. If the Elements box is checked, only the elements selected are rotated. If the Patterns box is also checked, existing patterns will also be rotated. If you want to rotate patterns with reference to elements, check only the Patterns box.
* 
Bitmap patterns and placed files containing bitmap patterns cannot be rotated.
You can conclude your entry with OK or by clicking the Copy button. In the latter case, the selection remains unchanged. Instead a copy of the selection is generated and is rotated in accordance with your specifications.
* 
When rotating a circle, the orientation angle is not changed. The original points of the element - insofar as these are still present - also remain unchanged. All the points of the element - including those resulting from intersections - are merely moved around the circumference.