Governing Equations
With cavitation transport models, the bulk motion of mixture of the liquid and gas (vapor and other possible gases) is treated as a variable density single-phase flow. The set of general governing equations for the mixture flow is the same as that for multicomponent flows, while a transport equation is specifically formed to govern the vapor mass fraction generated in cavitation. To model the effects of noncondensable gases, additional transport equations for gas mass fractions may also be solved, depending on the gas models. The complete set of general governing equations solved for cavitating flows follows:
• Continuity
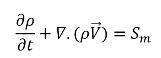
equation 2.166
where Sm is the net external or user source independent of cavitation
• Momentum Equations
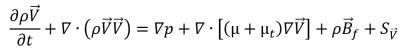
equation 2.167
• Energy Equation
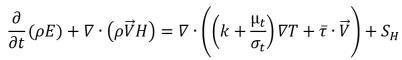
equation 2.168
• Vapor Mass Fraction Equation
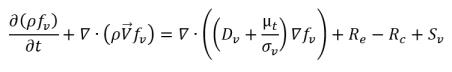
equation 2.169
where,
fv | vapor mass fraction |
Re | vapor generation source (evaporation) |
Rc | sink term (condensation) |
Sv | external or user-defined vapor source term |
• Noncondensable Gas (NCG) Mass Fraction Equation(s)
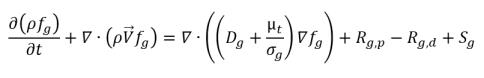
equation 2.170
This is a general transport equation for noncondensable gases (NCG), including generation, sink and external or user-defined source terms.
Depending on the cavitation models, different equations (between zero and two) are solved as noncondensable gas, dissolved gas, and so on.
For turbulent flows, the turbulent viscosity μt is obtained from solving the turbulence modeling equations. The turbulent Prandtl numbers σt, σv, σ g are predescribed model parameters. The details of the turbulence models are given in the Turbulence module.
In the transport equations, the mixture properties are calculated using the following relations:
• Mixture Density
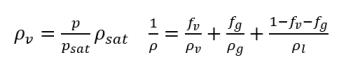
equation 2.171
where,
ρv | density of vapor |
ρg | density of noncondensable free gas |
ρl | density of liquid |
The liquid and vapor density are constant (incompressible), variable (compressible), or both. However, the noncondensable free gas density is always considered as an ideal gas in the cavitation models. Note that in equation 2.171, the liquid mass fraction ƒl is computed using the physical constraint: the mass fractions of all the components sum to unit, which follows below:
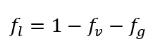
equation 2.172
In cavitating flows, the parameter of interest is the vapor αv or total gas-phase volume fraction αtotal which are deduced from the solved mass fraction ƒv and the free gas mass fraction ƒg:

equation 2.173
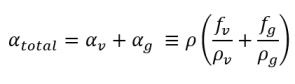
equation 2.174
• Mixture Viscosity
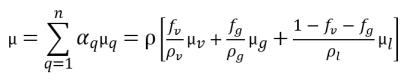
equation 2.175
where,
μv | dynamic viscosity of vapor |
μg | noncondensable free gas |
μl | liquid |
• Mixture Thermal Properties
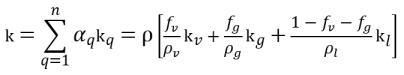
equation 2.176
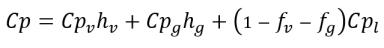
equation 2.177
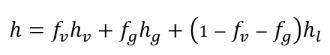
equation 2.178
where,
k | thermal conductivity |
Cp | specific heat for a constant pressure process |
h | specific enthalpy |
The components involved are denoted with specific subscripts for vapor (v), noncondensable free gas (g), and liquid (l).