Модели потока
Модуль Поток (Flow) ищет решение с учетом сохранения массы и импульса с помощью нестационарных уравнений Навье - Стокса H.Ding, F.C. Visser, Y.Jiang, and M. Furmanczyk, "Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications", FEDSM2009-78256, 2009..
Интегральная (консервативная) форма Рейнольдса для усредненных уравнений Навье - Стокса (RANS) имеет вид:
• Непрерывность
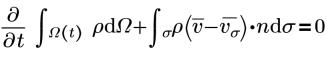
• Импульс
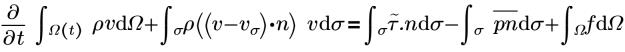
• Тензор напряжений
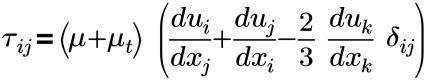
где
τij | Эффективное напряжение сдвига (молекулярное + турбулентное) |
f | Объемная сила |
n | Нормаль к поверхности |
ρ | Статическое давление (Па) |
t | время |
v | Скорость жидкости |
vσ | Скорость сетки |
Ω(t) | Контрольный объем как функция времени |
r | Средняя локальная плотность жидкости (кг/м3) |
σ | Поверхность контрольного объема |
µ | Динамическая вязкость (Пуаз или Па-с), |
µt | Турбулентная динамическая вязкость |
δij | Дельта Кронекера (=1 для i=j, =0 для i≠j) |
Модели вязкости
• Постоянная динамическая вязкость (Constant Dynamic Viscosity) - определяет вязкость жидкости в выбранном объеме. Единицей измерения динамической вязкости является Па-с или Н-с/м2.
Значение динамической вязкости указывается в поле при выборе опции Постоянная динамическая вязкость (Constant Dynamic Viscosity).
• Постоянная кинематическая вязкость (Constant Kinematic Viscosity) - определяет вязкость жидкости в выбранном объеме. Единицей измерения кинематической вязкости является м2/с. Значение кинематической вязкости указывается в поле при выборе опции Постоянная кинематическая вязкость (Constant Kinematic Viscosity).
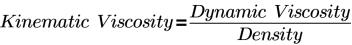
• Закон Сатерленда (Sutherland Law)- определяет вязкость жидкости в выбранном объеме через динамическую вязкость (Па-с). Уравнение и входные параметры имеют следующий вид:
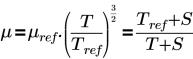
где
T | Температура (К) |
µref | Вязкость при опорной температуре (Па-с) |
S | Температура Сатерленда (К) |
T - температура жидкости (К) требуется как входной параметр, если модуль энергии не является активным. |
Закон Сатерленда используется для расчета вязкости идеального газа как функция температуры. Sutherland, W. (1893), "The viscosity of gases and molecular force," Philosophical Magazine, S. 5, 36, стр. 507-531 (1893). Следующая таблица показывает константу Сазерленда и опорную температуру для выбранных газов. Ссылка: en.wikipedia.org/wiki/viscosity.
Газ | S (К) | Tref (К) | mref (Па-с) |
|---|---|---|---|
Воздух | 120 | 291.15 | 18.27 e-6 |
Азот | 111 | 300.55 | 17.81 e-6 |
Кислород | 127 | 292.25 | 20.81 e-6 |
Углекислый газ | 240 | 293.15 | 14.8 e-6 |
Окись углерода | 118 | 288.15 | 17.2 e-6 |
Водород | 72 | 293.85 | 8.76 e-6 |
Аммиак | 370 | 293.15 | 9.82 e-6 |
Двуокись серы | 416 | 293.65 | 12.54 e-6 |
Гелий | 79.4 | 273 | 19 e-6 |
Неньютоновские модели вязкости
Имеются следующие неньютоновские модели вязкости:
• Модель Гершеля - Балкли
• Модели Бингама
Эти модели предоставляют соответствующую вязкость для различных типов жидкостей, которые демонстрируют свойства неньютоновских потоков. Модель Гершеля - Балкли и модели Бингама связывают напряжение сдвига со скоростью сдвига следующим образом:
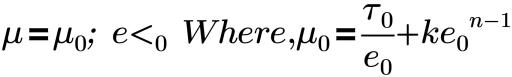
где
e0 | Критическая скорость сдвига |
k | Коэффициент консистенции |
τ0 | Предел текучести жидкости |
n | Показатель степени. Для модели Бингама n = 1 |
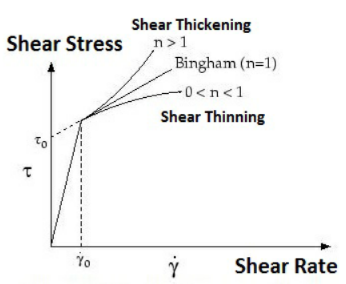
Скорость сдвига 0 совпадает с гамма-точкой на графике выше. |
Модель сопротивления
Модель сопротивления (Resistance Model) является опцией модуля Поток (Flow), которую можно использовать, чтобы задать сопротивление в выбранном объеме. Модель сопротивления (Resistance Model) содержит следующие две модели:
• Падение давления (Pressure Loss) - основывается на следующем уравнении:
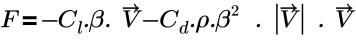
где
Cl | Линейный коэффициент сопротивления (Па-с/м2) |
Cd | Квадратичный коэффициент сопротивления (1/м) |
β | Пористость |
ρ | Плотность |
• Закон Дарси (Darcy's Law) - модель основывается на следующем уравнении:
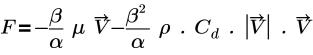
где
β | Пористость |
α | Проницаемость |
µ | Динамическая вязкость |
V | скорость |
Cd | Квадратичный коэффициент сопротивления (1/м) |
Скорость, используемая в уравнении сопротивления, является локальной скоростью. F в уравнении измеряется в единицах Н/м3, таких как сила/объем, градиент давления (Dp/Dx) или rg. Падение давления на интерфейсе рассчитывается умножением F на конечную толщину. Пористость задается в модуле Общие (Common).