静解析の問題

解析タイプ:	静解析
モデルタイプ:	2D 軸対称
比較対象:	NASTRAN No. V2411
参考文献:	• P.E. Grafton and D.R. Strome, "Analysis of Axisymmetrical Shells by the Direct Stiffness Method," AIAA Journal, 1(10): 2342-2347. • J.W. Jones and H.H. Fong, "Evaluation of NASTRAN," Structural Mechanics Software Series, Vol. IV (N. Perrone and W. Pilkey, eds.), 1982.
説明:	軸対称にモデル化された片持ち円柱の荷重が加わった端における半径方向のたわみを求めます。

要素 B は任意ですが、荷重が加えられている端付近の結果の精度を上げて計算時間を短縮するため、ここでは使用されています。

仕様

要素のタイプ:	2D シェル (2)
単位:	IPS
寸法:	長さ: 6 半径: 5 厚み: 0.01
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件	点 A に適用: すべての自由度を固定
荷重:	点 C に適用: FX = 1 分布: N/A 空間的変化: N/A

結果データの比較

	理論値	MSC/NASTRAN	Structure	差 (%)
荷重あたりの半径方向たわみ	2.8769e-3	2.8715e-3	2.8725e-3	0.15%
収束 %: ローカル変位/歪みエネルギーについて 0.5 %			最大次数: 7	方程式の数: 33

mvss002: フラット円形プレートの 2D 軸対称モデル

解析タイプ:	静解析
モデルタイプ:	2D 軸対称
比較対象:	ANSYS No. 15
参考文献:	Timoshenko, S. Strength of Materials, Part II, Advanced Theory and Problems.第 3 版NY:D. Van Nostrand Co., Inc. 1956, pp.96, 97, and 103.
説明:	軸対称にモデル化されたフラット円形プレートに、さまざまなエッジ拘束条件およびサーフェス荷重が適用されています。各ケースにおける最大応力を求めます。

仕様

要素のタイプ:	2D シェル (1)
単位:	IPS
寸法:	半径: 40 厚み: 1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件:	場所	自由度
クランプ	点 B に適用:	すべての自由度を固定
単純	点 B に適用:	X 方向と Y 方向の直線移動を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
クランプ	エッジ AB に適用: FY = 6	単位面積あたり	一様
単純	エッジ AB に適用: FY = 1.5	単位面積あたり	一様

結果データの比較

	理論値	ANSYS	Structure	差 (%)
最大応力 (m=max_prin_mag、a=clamped)	7200	7152	7200	0.0%
収束 %: ローカル変位/歪みエネルギーについて 0.0 %			最大次数: 5	方程式の数: 15
最大応力 (m=max_prin_mag、a=simple)	2970	2989	29701	0.0%
収束 %: ローカル変位/歪みエネルギーについて 0.0 %			最大次数: 5	方程式の数: 16

1 結果の符合は荷重の方向によって異なります。

mvss003: 2D 平面応力片持ちプレート

解析タイプ:	静解析
モデルタイプ:	2D 平面応力
比較対象:	NASTRAN No. V2408A
参考文献:	Singer, Ferdinand L. Strength of Materials.Harper & Row, 1962, Art. 52, p. 133.
説明:	平面内せん断荷重が加わった片持ちプレートの固定された端における曲げ応力を求めます。

仕様

要素のタイプ:	2D 応力 (1)
単位:	IPS
寸法:	長さ: 3 高さ: 0.6 厚み: 0.1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1.07e7	ポアソン比: 0 熱膨張: 0 熱伝導率: 0
拘束条件:	エッジ AB に適用: X 方向と Y 方向の直線移動を固定
荷重:	エッジ CD に適用: FY = -200 分布: 単位長さあたり空間的変化: 一様
理論上の結果はビームの基本理論に基づいています。Structure では、拘束条件が適用されているコーナーにおける特異応力を取り込むことで、実際の物理構造がモデル化されます。ポアソン比をゼロに設定すると、モデルがその基本形式に還元されます。

結果データの比較

	理論値	MSC/NASTRAN	Structure	差 (%)
節点 A における曲げ応力 (m=max_stress_xx)	6.0e4	5.5190e4	6.0121e4	0.20%
収束 %: ローカル変位/歪みエネルギーについて 0.0 %			最大次数: 4	方程式の数: 22

mvss004: ウォールが厚い円柱の 2D 平面歪みモデル

解析タイプ:	静解析
モデルタイプ:	2D 平面歪み
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	対称にモデル化されたウォールの厚い円柱に単位内圧が加わっています。2 つのほとんど圧縮できない材料の内側半径における半径方向の変位を求めます。

仕様

要素のタイプ:	2D ソリッド (1)
単位:	IPS
寸法:	外側半径: 9.0 内側半径: 3.0
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1000	ポアソン比: • 0.49 (ケース 1) • 0.499 (ケース 2)
拘束条件 (UCS):	エッジ AB と CD に適用: R 方向の直線移動以外のすべての自由度を固定
荷重:	エッジ AD に適用: 圧力荷重 = 1 分布: N/A 空間的変化: 一様

結果データの比較

	理論値	Structure	差 (%)
内側半径における半径方向変位 (ケース 1) (m=rad_disp)	5.0399e-3	5.0394e-3	<0.01%
収束 %: ローカル変位/歪みエネルギーについて 1 %		最大次数: 6	方程式の数: 38
内側半径における半径方向変位 (ケース 2) (m=rad_disp)	5.0602e-3	5.0553e-3	0.09%
収束 %: ローカル変位/歪みエネルギーについて 1.0 %		最大次数: 6	方程式の数: 38

mvss005: ウォールが厚い円柱の 2D 軸対称モデル

解析タイプ:	静解析
モデルタイプ:	2D 軸対称
比較対象:	NASTRAN No. V2410
参考文献:	Crandall S.H., Dahl N.C. , and Larnder T.J. An Introduction to the Mechanics of Solids.第 2 版 NY:McGraw-Hill Book Co., 1972, pp.293-297.
説明:	半径 r = 6.5" および r = 11.5" における応力を求めます。ウォールの厚い円柱が軸対称にモデル化され、内圧が加わっています。

仕様

要素のタイプ:	2D ソリッド (3)
単位:	IPS
寸法:	内側半径: 6 高さ: 8 厚み: 6
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0 熱膨張: 0 熱伝導率: 0
拘束条件 (UCS):	エッジ AD と BC に適用: Y 方向の直線移動と Z 軸を中心とした回転を固定
荷重:	エッジ AB に適用: 圧力荷重 = 10 分布: 単位面積あたり空間的変化: 一様

結果データの比較

		理論値	MSC/NASTRAN	Structure	差 (%)
@ r = 6.5	半径方向応力 (m=r6_5_radial)	-8.03	-8.05	-7.9720	0.72%
@ r = 6.5	円周方向応力 (m=r6_5_hoop)	14.69	14.73	14.69	0.0%
@ r = 11.5	半径方向応力 (m=r11_5_radial)	-0.30	-0.30	-2.6636e-1	0.0%
@ r = 11.5	円周方向応力 (m=r11_5_hoop)	6.96	6.96	6.96	0.0%
収束 %: ローカル変位/歪みエネルギーについて 0.25 %			最大次数: 4	方程式の数: 54

mvss006: 片持ちビームの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	NASTRAN No. V2405
参考文献:	Roark, R.J., and Young, W.C. Formulas for Stress and Strain.NY:McGraw-Hill Book Co., 1982, p. 96.
説明:	片持ちビームの自由端に荷重が加わっています。自由端におけるたわみと固定端における曲げ応力を求めます。

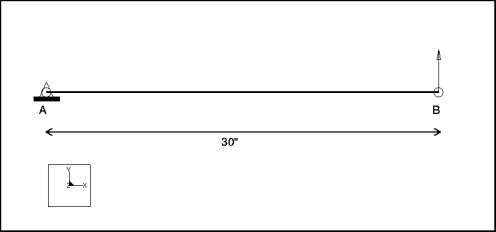
仕様

要素のタイプ:	ビーム (1)
単位:	IPS
寸法:	長さ: 30
ビーム特性:	面積: 0.310 IYY: 0.0241 せん断 FY: 1000 1 CY: 0.5	J: 0.0631 IZZ: 0.0390 せん断 FZ: 1000 1 CZ: 0.375
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1.0e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	点 B に適用: FY=100 分布: N/A 空間的変化: N/A

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較

	理論値	MSC/NASTRAN	Structure	差 (%)
先端におけるたわみ (m=max_disp_y)	2.3077	2.3077	2.3094	0.073%
固定端における曲げ応力 (m=max_beam_bending)	38461	38461	38461	0.0%
収束 %: ローカル変位/歪みエネルギーについて 0.0 %			最大次数: 4	方程式の数: 24

mvss007: 複数の拘束条件が適用されたビームの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	ANSYS No. 2
参考文献:	Timoshenko, S. Strength of Materials, Part I, Elementary Theory and Problems.第 3 版NY:D. Van Nostrand Co., Inc., 1955, p. 98, Problem 4.
説明:	下図のように支持された標準 30" WF ビームのオーバーハングに一様に荷重が加わっています。ビームの中央における最大曲げ応力と最大たわみを求めます。

仕様

要素のタイプ:	ビーム (4)
単位:	IPS
寸法:	長さ: 480
ビーム特性:	面積: 50.65 IYY: 1 せん断 FY: 0.8333 CY: 15	J: 7893 IZZ: 7892 せん断 FZ: 0.8333 CZ: 15
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
	点 B に適用: 点 D に適用:	Y 軸を中心とした回転と Z 軸を中心とした回転以外のすべての自由度を固定 Y 方向の直線移動と Z 方向の直線移動を固定

荷重	位置/マグニチュード	分布	空間的変化
	エッジ AB に適用: FY = 833.33 エッジ DE に適用: FY = 833.33	単位長さあたり単位長さあたり	一様一様

結果データの比較

	理論値	ANSYS	Structure	差 (%)
中央における最大曲げ応力 (m=max_beam_bending)	11400	11404	11403.91	0.03%
中央における最大たわみ (m=disp_center)	0.182	0.182	0.182	0.0%
収束 %: ローカル変位/歪みエネルギーについて 0.0 %			最大次数: 4	方程式の数: 96

mvss008: 平行四辺形のシェル要素を使用したビームの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	平行四辺形要素を使用してモデル化されている直線片持ちビームの自由端に、以下に示す 4 種類の単位荷重が加わっています。 • 引張り荷重 • 平面内せん断荷重 • 平面外せん断荷重 • ねじれ荷重各ケースにおける先端部の荷重方向への変位を求めます。

仕様

要素のタイプ:	シェル (3)
単位:	IPS
寸法:	長さ: 6 幅: 0.2 厚み: 0.1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	エッジ AD に適用: すべての自由度を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
引張り荷重	エッジ BC に適用: FX = 1	全荷重	一様
平面内荷重	エッジ BC に適用: FY = 1	全荷重	一様
平面外荷重	エッジ BC に適用: FZ = 1	全荷重	一様
ねじれ荷重	点 E に適用: MX = 1	全荷重	N/A

結果データの比較

	理論値	Structure	差 (%)
先端部の荷重方向への変位 (l=extension, m=max_disp_x)	3e-5	2.998e-5	0.06%
先端部の荷重方向への変位 (l=in_plane, m=max_disp_y)	0.1081	0.1078	0.27%
先端部の荷重方向への変位 (l=out_plane, m=max_disp_z)	0.4321	0.4309	0.27%
先端部の荷重方向への変位 (l=twist, m=max_rot_x)	0.03408 1	0.03424	0.46%
収束 %: ローカル変位/歪みエネルギーについて 0.9 %		最大次数: 6	方程式の数: 396

1 MacNeal-Harder の Table 3 (p. 10) に掲載されている直線ビームのねじれ荷重に誤植があります。これは正しくは 0.03408 になります。

mvss009: 台形のシェル要素を使用したビームの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	台形要素を使用してモデル化されている直線片持ちビームの自由端に、以下に示す 4 種類の単位荷重が加わっています。 • 引張り荷重 • 平面内せん断荷重 • 平面外せん断荷重 • ねじれ各ケースにおける先端部の荷重方向への変位を求めます。

仕様

要素のタイプ:	シェル (3)
単位:	IPS
寸法:	長さ: 6 幅: 0.2 厚み: 0.1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	エッジ AD に適用: すべての自由度を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
引張り荷重	エッジ BC に適用: FX = 1	全荷重	一様
平面内荷重	エッジ BC に適用: FY = 1	全荷重	一様
平面外荷重	エッジ BC に適用: FZ = 1	全荷重	一様
ねじれ荷重	点 E に適用: MX = 1	全荷重	N/A

結果データの比較

	理論値	Structure	差 (%)
先端部の荷重方向への変位 (l=extension、m=max_disp_x)	3e-5	2.998e-5	0.08%
先端部の荷重方向への変位 (l=in_plane、m=max_disp_y)	0.1081	0.1079	0.32%
先端部の荷重方向への変位 (l=out_plane、m=max_disp_z)	0.4321	.4311	0.23%
先端部の荷重方向への変位 (l=twist、m=max_rot_x)	0.03408 1	0.03381	0.79%
収束 %: ローカル変位/歪みエネルギーについて 0.7 %		最大次数: 6	方程式の数: 906

1 MacNeal-Harder の Table 3 (p. 10) に掲載されている直線ビームのねじれ荷重に誤植があります。これは正しくは 0.03408 になります。

mvss010: シェルを使用してモデル化されたカーブビームの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	90の円弧の形状をしたカーブビームは、一方の端が固定され、もう一方の端は解放されています。このビームの自由端に平面内荷重と平面外荷重を加えた場合の、先端部の荷重方向への変位を求めます。

仕様

要素のタイプ:	シェル (2)
単位:	IPS
寸法:	外側半径: 4.32 内側半径: 4.12 厚み: 0.1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1e7	ポアソン比: 0.25 熱膨張: 0 熱伝導率: 0
拘束条件:	エッジ AD に適用: すべての自由度を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
平面内荷重	エッジ BC に適用: FY = 1	全荷重	一様
平面外荷重	エッジ BC に適用: FZ = 1	全荷重	一様

結果データの比較

	理論値	Structure	差 (%)
先端部の荷重方向への変位 (l=in_plane、m=tip_disp_y)	0.08734	0.08833	1.13%
先端部の荷重方向への変位 (l=out_plane、m=tip_disp_z)	0.5022	0.50057	0.32%
収束 %: ローカル変位/歪みエネルギーについて 0.3 %		最大次数: 6	方程式の数: 234

mvss011: 単純支持された長方形プレートの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	フラットプレートが 4 つのエッジすべてで単純支持されています。対称性を利用してプレートの 1/4 モデルが作成されています。このプレートには、一様な圧力荷重と中心への点荷重の 2 種類の荷重が加わっています。プレートの中央における変位を求めます。

仕様

要素のタイプ:	シェル (2)
単位:	IPS
寸法:	長さ: 5 幅: 1 厚み: 0.0001
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1.7472e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
	エッジ AD と CD に適用: エッジ AB に適用: エッジ BC に適用:	X 方向の直線移動、Y 方向の直線移動、Z 方向の直線移動を固定 Y 方向の直線移動、X 軸を中心とした回転、Z 軸を中心とした回転を固定 X 方向の直線移動、Y 軸を中心とした回転、Z 軸を中心とした回転を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
圧力荷重	すべてのシェルに適用: 圧力 = 1e4	単位面積あたりの全荷重	一様
点荷重	B に適用: FZ = 1e4	N/A	N/A

結果データの比較

	理論値	Structure	差 (%)
中心における変位 (l=pressure、m=disp_z_cen)	12.97	12.97	0.0%
中心における変位 (l=point、m=disp_z_cen)	16.96	16.81	0.88%
収束 %: ローカル変位/歪みエネルギーについて 0.8 %		最大次数: 9	方程式の数: 438

mvss012: クランプされた長方形プレートの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	4 本のエッジがクランプされた長方形プレートの 1/4 モデルが対称性を利用して作成されています。このプレートには、一様な圧力荷重と中心への点荷重の 2 種類の荷重が加わっています。プレートの中央における変位を求めます。

仕様

要素のタイプ:	シェル (2)
単位:	IPS
寸法:	長さ: 5 幅: 1 厚み: 0.0001
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 1.7472e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
	エッジ AD と DC に適用: エッジ AB に適用: エッジ BC に適用:	すべての自由度を固定 Y 方向の直線移動、X 軸を中心とした回転、Z 軸を中心とした回転を固定 X 方向の直線移動、Y 軸を中心とした回転、Z 軸を中心とした回転を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
圧力荷重	すべてのシェルに適用: 圧力 = 1e4	単位面積あたり	一様
点荷重	B に適用: FZ = 1e4	N/A	N/A

結果データの比較

	理論値	Structure	差 (%)
中心における変位 (l=pressure、m=measure1)	2.56	2.604	1.71%
中心における変位 (l=point、m=measure1)	7.23	7.168	0.85%
収束 %: ローカル変位/歪みエネルギーについて 1.3 %		最大次数: 9	方程式の数: 625

mvss013: 半球シェルの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	赤道上に 90間隔で荷重方向が交互に逆となる点荷重が加わった、開いた半球の 1/4 モデルが対称性を利用して作成されています。任意の荷重点における半径方向の変位を求めます。

仕様

要素のタイプ:	シェル (4)
単位:	IPS
寸法: (1/4 モデルを使用)	半径: 10 円弧範囲: 90o 厚み: 0.04
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 6.825e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
	カーブ AC に適用: カーブ GE に適用: 点 D に適用:	P 方向の直線移動、R 軸を中心とした回転、T 軸を中心とした回転を固定 P 方向の直線移動、R 軸を中心とした回転、T 軸を中心とした回転を固定 T 方向の直線移動を固定

荷重:	位置/マグニチュード:	分布:	空間的変化
	点 C に適用: FR = 1 E に適用: FR = 1	N/A N/A	N/A N/A

結果データの比較

	理論値	Structure	差 (%)
荷重あたりの半径方向の変位 (m=disp_rad)	0.0924	0.0933	0.97%
収束 %: ローカル変位/歪みエネルギーについて 0.6 %		最大次数: 9	方程式の数: 1965

mvss014: 90

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	90ねじれた片持ちビームの自由端に、平面内荷重と平面外荷重が加わっています。各ケースにおける先端部の荷重方向への変位を求めます。

仕様

要素のタイプ:	ソリッド (2)
単位:	IPS
寸法:	長さ: 12 幅: 1.1 厚み: 0.32 ねじれの角度: 90o (固定端から自由端まで)
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 29e6	ポアソン比: 0.22 熱膨張: 0 熱伝導率: 0
拘束条件:	根元のサーフェスに適用: すべての自由度を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
平面内荷重	自由端サーフェスに適用: FY = 1	全荷重	一様
平面外荷重	自由端サーフェスに適用: FZ = 1	全荷重	一様

結果データの比較

	理論値	Structure	差 (%)
先端部の荷重方向への変位 (l=in_plane、m=disp_tip_y1)	0.005424	0.005428	0.73%
先端部の荷重方向への変位 (l=out_of_plane、m=disp_tip_z1)	0.001754	0.001760	0.342%
収束 %: ローカル変位/歪みエネルギーについて 0.8 %		最大次数: 5	方程式の数: 590

mvss015: Scordelis-Lo 屋根の 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	MacNealHarder 精度テスト
参考文献:	MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985.
説明:	Scordelis-Lo 屋根は対称性を利用してモデル化されたアーチ構造の屋根であり、一様に荷重が加わっています。(屋根全体の) 直線の側の中心点における垂直方向の変位を求めます。

仕様

要素のタイプ:	シェル (1)
単位:	IPS
寸法: (1/4 モデルを使用)	長さ: 25 半径: 25 円弧範囲: 40o 厚み: 0.25
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 4.32e8	ポアソン比: 0 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
(UCS) (UCS) (UCS)	カーブ AB に適用: カーブ AD に適用: カーブ CD に適用:	Z 方向の直線移動、R 軸を中心とした回転、T 軸を中心とした回転を固定 T 方向の直線移動、Z 軸を中心とした回転、R 軸を中心とした回転を固定 R 方向の直線移動と T 方向の直線移動を固定

荷重:	位置/マグニチュード:	分布:	空間的変化:
	面 ABCD に適用: FZ = 90	単位面積あたり	一様

結果データの比較

	理論値	Structure	差 (%)
点 B における垂直方向の変位 (m=disp_z_mid)	0.3024	0.3008	0.53%
収束 %: ローカル変位/歪みエネルギーについて 0.2 %		最大次数: 7	方程式の数: 148

mvss016: 円柱/球体の 2D 軸対称モデル

解析タイプ:	静解析
モデルタイプ:	2D 軸対称
参考文献:	NAFEMS, LSB1, No. IC 39
説明:	軸対称の円柱と半球からなる容器に一様な内圧が加わっています。外側サーフェス上の点 D における円周方向応力を求めます。

仕様

要素のタイプ:	2D シェル (4)
単位:	MKS
寸法:	半径: 1 厚み: 0.025
材料特性:	質量密度: 0.007 単位質量あたりのコスト: 0 ヤング率: 210000	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
拘束 1	点 A に適用: 点 E に適用:	X 方向の直線移動と Z 軸を中心とした回転を固定 Y 方向の直線移動を固定

荷重:	位置/マグニチュード:
荷重 1	すべての 2D シェル要素に適用: 内圧 = 1

結果データの比較

	理論値	Structure1	差 (%)
外側サーフェス上の Szz	38.5	38.62	0.3%
収束 %: ローカル変位/歪みエネルギーについて 0.8 %		最大次数: 7	方程式の数: 72

1. サマリーファイルの結果情報は表示できません。結果を表示するには、応力 ZZ (下側) の結果表示ウィンドウを定義し、点 D における値をクエリーする必要があります。

mvss017: 重力荷重が加わったテーパー付き薄膜の 2D モデル

解析タイプ:	静解析
モデルタイプ:	平面応力
参考文献:	NAFEMS, LSB1, No. IC 2
説明:	テーパー付き薄膜でグローバル X 方向に一様な加速度が生じています。点 B における直接応力 Sxx を求めます。

仕様

要素のタイプ:	2D 応力 (2)
単位:	MKS
寸法:	厚み: 0.1
材料特性:	質量密度: 0.007 単位質量あたりのコスト: 0 ヤング率: 210000	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件:	場所	自由度
拘束 1	カーブ AB、BC に適用: 点 B に適用:	X 方向の直線移動を固定 X 方向と Y 方向の直線移動を固定

荷重:	位置/マグニチュード:
荷重 1	グローバル加速度: GX=9.81

結果データの比較

	理論値	Structure	差 (%)
点 B における応力 XX (m=measure1)	0.247	0.247	0%
収束 %: ローカル変位/歪みエネルギーについて 0.7 %		最大次数: 7	方程式の数: 248

mvss018: Z 断面片持ちプレートの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
参考文献:	NAFEMS, LSB1, No. IC 29
説明:	Z 断面片持ちプレートの自由端に、2 つの均一に分散されたエッジせん断によるトルクが加わっています。プレートの中間平面における直接応力 Sxx を求めます。

仕様

要素のタイプ:	シェル (6)
単位:	MKS
寸法:	長さ: 10 厚み: 0.1
材料特性:	質量密度: 0.007 単位質量あたりのコスト: 0 ヤング率: 210000	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
拘束 1	カーブ AB、BC、CD に適用:	X 方向の直線移動、Y 方向の直線移動、Z 方向の直線移動を固定

荷重:	位置/マグニチュード:	分布	空間的変化
荷重 1	カーブ EF に適用: FZ=0.6 カーブ GH に適用: FZ=0.6	全荷重全荷重	一様一様

結果データの比較

	理論値	Structure1	差 (%)
中間サーフェスの点 M における Sxx	108.8	110.02	1.1%
収束 %: ローカル変位/歪みエネルギーについて 0.4 %		最大次数: 7	方程式の数: 870

1. サマリーファイルの結果情報は表示できません。結果を表示するには、応力 XX (上側と下側) のメジャーの結果表示ウィンドウを定義し、点 M における値をクエリーする必要があります。次に、上側 (118) と下側 (105.56) の値の平均を求めます。

mvss019: エッジにモーメントを加えた円柱シェルの 3D モデル

解析タイプ:	静解析
モデルタイプ:	3D
参考文献:	NAFEMS, LSB1, No. IC 19
説明:	3D 空間内の円柱シェルの 1 本のエッジに一様な法線エッジモーメントが加えられています。外側サーフェスの点 E における接線方向応力を求めます。

仕様

要素のタイプ:	シェル (1)
単位:	MKS
寸法:	半径: 1 厚み: 0.01
材料特性:	質量密度: 0.007 単位質量あたりのコスト: 0 ヤング率: 210000	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
拘束 1	カーブ AB に適用: カーブ AD と BC に適用:	すべての自由度を固定 Z 方向の直線移動、X 軸を中心とした回転、Y 軸を中心とした回転を固定

荷重:	位置/マグニチュード:	分布	空間的変化
荷重 1	カーブ CD に適用: MZ=0.001	単位長さあたりのフォース	一様

結果データの比較

	理論値	Structure1	差 (%)
外側サーフェスの点 E における Sxx	60.0	59.6	.67%
収束 %: ローカル変位/歪みエネルギーについて 0.9 %		最大次数: 5	方程式の数 : 66

1. サマリーファイルの結果情報は表示できません。結果を表示するには、「フェースグリッド」(Face Grid) をオンにして応力 XX (上側) のメジャーの結果表示ウィンドウを定義し、点 E における値をクエリーする必要があります。

mvss020: ビーム断面

解析タイプ:	静解析
モデルタイプ:	3D
比較対象:	理論値
参考文献:	Roark, R.J., and Young, W.C. Formulas for Stress and Strain.5th Edition.NY:McGrawHill Book Co. 1982, p. 64.
説明:	片持ちビームに Y 方向と Z 方向の横荷重と X 方向の軸荷重が加わっています。自由端におけるたわみ、固定端における曲げ応力、およびビームに沿った軸応力を求めます。

このビーム断面モデルには、以下の要素タイプとそれに対応する結果が含まれています。

すべてのケースで、変位の結果は荷重の方向によって異なります。したがって、この問題では、「先端におけるたわみ」に一覧されている結果は、正と負どちらの値としても解釈できます。

正方形ビーム

仕様

要素のタイプ:	正方形ビーム
単位:	IPS
寸法:	a: 0.25
ビーム特性:	面積: 0.0625 IYY: 0.000325521 せん断 FY: 1000 1 CY: 0.125	J: 0.000549316 IZZ: 0.000325521 せん断 FZ: 1000 1 CZ: 0.125
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (正方形ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	sq_d_x	1.6e-3	1.6e-3	0%
横軸方向 (y)	sq_d_y	9.216e1	9.216e1	0%
横軸方向 (z)	sq_d_z	9.216e1	9.216e1	0%
応力:
軸方向	sq_s_ten	1.6e3	1.6e3	0%
横軸方向 (y)	sq_s_bnd	1.152003e6	1.15200e6	0%
横軸方向 (z)	sq_s_bnd	1.152003e6	1.15200e6	0%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

長方形ビーム

仕様

要素のタイプ:	長方形ビーム
単位:	IPS
寸法:	b: 1 d: 0.25
ビーム特性:	面積: 0.25 IYY: 0.0208333 せん断 FY: 1000 1 CY: 0.125	J: 0.00438829 IZZ: 0.00130208 せん断 FZ: 1000 1 CZ: 0.5
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (長方形ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	rct_d_x	4e-4	4e-4	0 %
横軸方向 (y)	rct_d_y	2.304e1	2.304e1	0 %
横軸方向 (z)	rct_d_z	1.44	1.44	0 %
応力:
荷重	メジャー名	理論値	Structure	差 (%)
軸方向	rct_s_ten	4.0e2	4.0e2	0 %
横軸方向 (y)	rct_s_bnd	2.880e5	2.880e5	0 %
横軸方向 (z)	rct_s_bnd	7.200e4	7.200e4	0 %

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0 %	2	264
横軸方向 (y)	0 %	2	264
横軸方向 (z)	0 %	2	264

中空長方形ビーム

仕様

要素のタイプ:	中空長方形ビーム
単位:	IPS
寸法:	b: 1 bi: 0.875 d: 0.25 di: 0.125
ビーム特性:	面積: 0.140625 IYY: 0.013855 せん断 FY: 1000 1 CY: 0.125	J: 0.00343323 IZZ: 0.00115967 せん断 FZ: 1000 1 CZ: 0.5
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (中空長方形ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	hrct_d_x	7.112e-4	7.111e-4	0.02%
横軸方向 (y)	hrct_d_y	2.5869e1	2.5876e1	0.027%
横軸方向 (z)	hrct_d_z	2.1653	2.1677	0.10%
応力:
荷重	メジャー名	理論値	Structure	差 (%)
軸方向	hrct_s_ten	7.112e2	7.111e2	0.01%
横軸方向 (y)	hrct_s_bnd	3.2337e5	3.2336e5	0.003%
横軸方向 (z)	hrct_s_bnd	1.0826e5	1.0826e5	0%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

溝形ビーム

仕様

要素のタイプ:	溝形ビーム
単位:	IPS
寸法:	b: 1 di: 1 t: 0.125 tw: 0.125
ビーム特性:	面積: 0.375 IYY: 0.0369466 せん断 FY: 1000 1 CY: 0.625	J: 0.00179932 IZZ: 0.0898438 せん断 FZ: 1000 1 CZ: 0.645833
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (溝形ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	chnl_d_x	2.6667e-4	2.666667e-04	0 %
横軸方向 (y)	chnl_d_y	3.339e-1	4.004507e-01	19.93 %
横軸方向 (z)	chnl_d_z	8.1198e-1	8.1198e-1	0 %
応力:
荷重	メジャー名	理論値	Structure	差 (%)
軸方向	chnl_s_ten	2.6667e2	2.6667e2	0 %
横軸方向 (y)	chnl_s_bnd	2.087e4	2.087e4	0 %
横軸方向 (z)	chnl_s_bnd	5.244e4	5.244e4	0 %

収束:
荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
軸方向	0 %	4	264
横軸方向 (y)	0 %	4	264
横軸方向 (z)	0 %	4	264

I 形断面ビーム

仕様

要素のタイプ:	I 形断面ビーム
単位:	IPS
寸法:	b: 1 di: 1 t: 0.125 tw: 0.125
ビーム特性:	面積: 0.375 IYY: 0.0209961 せん断 FY: 1000 1 CY: 0.625	J: 0.00179932 IZZ: 0.0898438 せん断 FZ: 1000 1 CZ: 0.5
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (I 形断面ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	I_d_x	2.6667e-4	2.6667e-4	0%
横軸方向 (y)	I_d_y	3.3391e-1	3.3573e-1	0.54%
横軸方向 (z)	I_d_z	1.4288	1.4296	0.05%
応力:
荷重	メジャー名	理論値	Structure	差 (%)
軸方向	I_s_ten	2.6667e2	2.6667e2	0%
横軸方向 (y)	I_s_bnd	2.0870e4	2.0869e4	0.004%
横軸方向 (z)	I_s_bnd	7.1442e4	7.14418e4	0.001%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

L 形断面ビーム

仕様

要素のタイプ:	L 形断面ビーム
単位:	IPS
寸法:	b: 1 d: 1 t: 0.125 tw: 0.125
ビーム特性:	面積: 0.25 IYY: 0.0105794 せん断 FY: 1000 1 CY: 0.789352	J: 0.00119955 IZZ: 0.0423177 せん断 FZ: 1000 1 CZ: 0.433047
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (L 形断面ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	L_d_x	4e-4	4e-4	0%
横軸方向 (y)	L_d_y	7.0892e-1	7.089233e-01	0.0004 %
横軸方向 (z)	L_d_z	2.8357	2.835700	0%
応力:
荷重	メジャー名	理論値	Structure	差 (%)
軸方向	L_s_ten	4e2	4e2	0%
横軸方向 (y)	L_s_ben	5.5611e4	5.595900e+04	0.62%
横軸方向 (z)	L_s_ben	1.228e5	1.227991e+05	0.0007 %

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

ひし形ビーム

仕様

要素のタイプ:	ひし形ビーム
単位:	IPS
寸法:	b: 0.25 d: 0.25
ビーム特性:	面積: 0.03125 IYY: 8.13802e5 せん断 FY: 1000 1 CY: 0.125	J: 0.000146484 IZZ: 8.13802e5 せん断 FZ: 1000 1 CZ: 0.125
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (ひし形ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	dmnd_d_x	3.2e-3	3.2e-3	0%
横軸方向 (y)	dmnd_d_y	3.6864e2	3.6864e2	0%
横軸方向 (z)	dmnd_d_z	3.6864e2	3.6864e2	0%
応力:
荷重	メジャー名	理論値	Structure	差 (%)
軸方向	dmnd_s_ten	3.2e3	3.2e3	0%
横軸方向 (y)	dmnd_s_bnd	4.608e6	4.608e6	0%
横軸方向 (z)	dmnd_s_bnd	4.608e6	4.608e6	0%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

中実円ビーム

仕様

要素のタイプ:	中実円ビーム
単位:	IPS
寸法:	r: 0.25
ビーム特性:	面積: 0.19635 IYY: 0.00306796 せん断 FY: 1000 1 CY: 0.25	J: 0.00613592 IZZ: 0.00306796 せん断 FZ: 1000 1 CZ: 0.25
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (中実円ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	crcl_d_x	5.093e-4	5.092e-4	0.019%
横軸方向 (y)	crcl_d_y	9.77848	9.77995	0.015%
横軸方向 (z)	crcl_d_z	9.77848	9.77995	0.015%
応力:
軸方向	crcl_s_ten	5.093e2	5.092e2	0.019%
横軸方向 (y)	crcl_s_bnd	2.44462e5	2.44462e5	0%
横軸方向 (z)	crcl_s_bnd	2.44462e5	2.44462e5	0%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

中空円ビーム

仕様

要素のタイプ:	中空円ビーム
単位:	IPS
寸法:	ri: 0.25
ビーム特性:	面積: 0.147262 IYY: 0.00287621 せん断 FY: 10000 1 CY: 0.25	J: 0.00575243 IZZ: 0.00287621 せん断 FZ: 1000 1 CZ: 0.25
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (中空円ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	hcr_d_x	6.7906e-4	6.7906e-4	0%
横軸方向 (y)	hcr_d_y	1.04304e1	1.04331e1	0.025%
横軸方向 (z)	hcr_d_z	1.04304e1	1.04332e1	0.026%
応力:
軸方向	hcr_s_ten	6.7906e2	6.7906e2	0%
横軸方向 (y)	hcr_s_bnd	2.6076e5	2.6075e5	0.003%
横軸方向 (z)	hcr_s_bnd	2.6076e5	2.6076e5	—

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

楕円ビーム

仕様

要素のタイプ:	楕円ビーム
単位:	IPS
寸法:	a: 1 b: 0.25
ビーム特性:	面積: 0.785398 IYY: 0.19635 せん断 FY: 1000 1 CY: 0.25	J: 0.0461999 IZZ: 0.0122718 せん断 FZ: 1000 1 CZ: 1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (楕円ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	elps_d_x	1.2732e-4	1.2732e-4	0%
横軸方向 (y)	elps_d_y	1.527887e-1	1.531516e-01	0.24 %
横軸方向 (z)	elps_d_z	2.4446	2.445098	0.02%
応力:
軸方向	elps_s_ten	1.273239e2	1.27324e2	0%
横軸方向 (y)	elps_s_bnd	1.527887e4	1.527887e4	0%
横軸方向 (z)	elps_s_bnd	6.11155e4	6.111550e4	0%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

中空楕円ビーム

仕様

要素のタイプ:	中空楕円ビーム
単位:	IPS
寸法:	a: 1 b: 0.25 ai: 0.875
ビーム特性:	面積: 0.184078 IYY: 0.081253 せん断 FY: 1000 1 CY: 0.25	J: 0.0191184 IZZ: 0.00507832 せん断 FZ: 1000 1 CZ: 1
材料特性:	質量密度: 0 単位質量あたりのコスト: 0 ヤング率: 3e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0
拘束条件:	点 A に適用: すべての自由度を固定
荷重:	場所:	マグニチュード:
軸方向	点 B に適用	FX=100
横軸方向 (y)	点 B に適用	FY=100
横軸方向 (z)	点 B に適用	FZ=100

1. 構造ビームではせん断が考慮されますが、提示されている理論上の問題では考慮されていません。せん断係数の値によってこれを補正します。

結果データの比較 (中空楕円ビーム)

荷重	メジャー名	理論値	Structure	差 (%)
先端におけるたわみ:
軸方向	hel_d_x	5.4325e-4	5.4324e-4	0.0018%
横軸方向 (y)	hel_d_y	3.6922e-1	3.7091e-1	0.45%
横軸方向 (z)	hel_d_z	5.9075	5.9091	0.027%
応力:
軸方向	hel_s_ten	5.4325e2	5.4324e2	0.0018%
横軸方向 (y)	hel_s_bnd	3.6922e4	3.6921e4	0.0027%
横軸方向 (z)	hel_s_bnd	1.4769e5	1.4768e5	0.0067%

荷重	ローカル変位/歪みエネルギー	最大次数	方程式の数
収束:
軸方向	0%	2	264
横軸方向 (y)	0%	2	264
横軸方向 (z)	0%	2	264

mvss021: 内圧が加わっているウォールが厚いシリンダー

解析タイプ:	静解析
モデルタイプ:	3D
参考文献:	Roark, R.J., and Young, W.C. Formulas for Stress and Strain.NY:McGraw-Hill Book Co., 5th edition, Table 32, Case 1.
説明:	ウォールが厚い、内圧が加わっているシリンダーが、すべての方向に自由に膨張できます。半径方向と円周方向の最大応力を求めます。

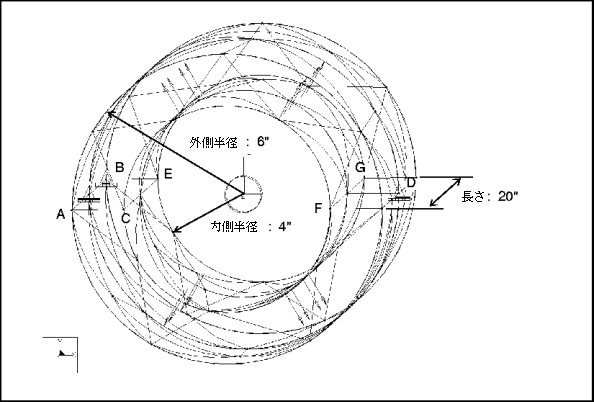
仕様

要素のタイプ:	四面体 (133)
単位:	IPS
寸法:	長さ: 20 Ro: 6 Ri: 4
材料特性:	質量密度: 0.0002614 単位質量あたりのコスト: 0 ヤング率: 1.06e7	ポアソン比: 0.33 熱膨張: 1.25e05 熱伝導率: 9.254

拘束条件	場所	自由度
拘束 1	点 A に適用: 点 B に適用: 点 D に適用:	X 方向の直線移動、Y 方向の直線移動、Z 方向の直線移動を固定 Y 方向の直線移動を固定 Y 方向の直線移動と Z 方向の直線移動を固定

荷重:	位置/マグニチュード:	分布	空間的変化
圧力荷重	すべての内側サーフェスに適用: 圧力 = 1000	単位面積あたりの全荷重	一様

結果データの比較

	理論値	Structure	差 (%)
エッジ CE および FG における 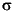yy	2600	2603.7325	0.14%
エッジ CE および FG における 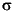xx	1000	999.1724	0.08%
マルチパス収束 %: 解析はメジャーについて 1 % 以内に収束。		最大次数: 6	方程式の数: 1875

mvss022: 自重が加わっているウォールが薄い球形容器

解析タイプ:	静解析
モデルタイプ:	3D 周期対称
参考文献:	Roark, R.J., and Young, W.C. Formulas for Stress and Strain.NY:McGraw-Hill Book Co., 5th edition, Table 29, Case 3c.
説明:	薄いウォールの半球容器にその自重 (重力荷重) が加わっています。点 A と点 B における円周方向応力を求めます。

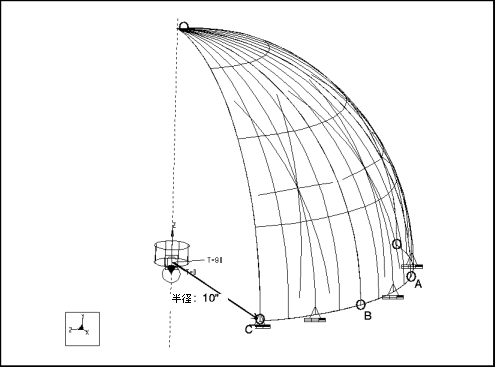
仕様

要素のタイプ:	シェル (3)
単位:	IPS
寸法:	R: 10
材料特性:	質量密度: 0.0002588 単位質量あたりのコスト: 0 ヤング率: 1.0e7	ポアソン比: 0.3 熱膨張: 0 熱伝導率: 0

拘束条件	場所	自由度
拘束 1	= 0 と = 90 のエッジに適用: z = 0 のエッジに適用: 点 C (r = 10, = 0, z = 0) に適用:	周期対称 Z 方向の直線移動を固定 R 方向の直線移動、T 方向の直線移動、Z 方向の直線移動を固定

荷重:	方向:	マグニチュード:
重力	x y Z	0.0 386.4 0.0

結果データの比較

	理論値	Structure	差 (%)
点 A における 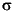zz:	1	0.987	1.3%
点 B における 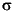tt:	-1	-0.982	1.8%
マルチパスアダプティブ収束精度 %: 解析はローカル変位および要素歪みエネルギーについて 4.9 % 以内に収束。解析はグローバル RMS 応力について 1.7 % に収束。		最大次数: 9	方程式の数 : 773

mvsl001: 複合レイアップの静解析

解析タイプ:	異方性材料特性での静解析
モデルタイプ:	3D
比較対象:	理論値
参考文献:	Noor, A.K. and Mathers, M.D., "Shear-Flexible Finite-Element Models of Laminated Composite Plates and Shells." NASA TN D-8044; Langley Research Center, Hampton, Va. Dec. 1975.
説明:	クランプされた 9 層の異方性正方形プレートにおける、最大合力曲げモーメントと横変形を求めます。

仕様

要素のタイプ:	シェル (4)
単位:	IPS
寸法:	長さ: 2.5 幅: 2.5 厚み: 0.5
シェル特性:
引張り剛性	A11=10.266	A12=0.1252	A16=0
		A22=10.266	A26=0
			A66=0.3
引張り曲げ結合剛性	B11=0	B12=0	B16=0
		B22=0	B26=0
			B66=0
曲げ剛性	D11=0.25965	D12=0.0026082	D16=0
		D22=0.1681	D26=0
			D66=0.00625
横せん断剛性	A55=0.275004	A45=0	A44=0.275004
単位面積あたりの質量	7.2915e5
単位面積あたりの回転慣性	1.5191e5
熱合成係数:
フォース	N11=0	N22=0	N12=0
モーメント	M11=0	M22=0	M12=0
応力計算位置	CZ	プライ方向 (度)	材料
"上側" の結果として報告された位置	0.25	0	trniso1
"下側" の結果として報告された位置	0.25	0	trniso1
材料特性:
質量密度: 0.00014583	単位質量あたりのコスト: 0
ヤング率	E1=4e1	E2=1	E3=1
ポアソン比	Nu21=0.25	Nu31=0.25	Nu32=0
横せん断係数	G21=0.6	G31=0.6	G32= E2/[2*(1+Nu32)]
熱膨張係数	a1=0	a2=0	a3=0
拘束条件:	エッジ BC と CD に対称拘束条件を適用エッジ AB と AD をクランプ
荷重:	サーフェス全体への一様な圧力荷重 = 1

結果データの比較

	理論値	Structure	差 (%)
変位	11.596	11.84151	2.11%
曲げモーメント1	1.4094	1.41307	0.26%
収束 %: ローカル変位および要素歪みエネルギーについて 1.1 % およびグローバル RMS 応力について 2.2 %		最大次数: 3	方程式の数: 76

1 この Creo Simulate の結果を確認するには、量 "モーメント: シェル合力: XX" についての結果表示ウィンドウを作成してクエリーします。結果表示ウィンドウを開き、モデルの左上隅で値をクエリーします。この値は「ビュー」(View) > 「モデル最小」(Model Min) を使用して取得します。この負の値の絶対値がここで報告され、この値は「ビュー」(View) > 「モデル最大」(Model Max) を使用したときに報告された値よりも大きくなります。

これは役に立ちましたか?