輻射熱伝達のモデリング
熱流体系において、ソリッドサーフェス、流体流れ、またはソリッドサーフェスと流体流れの両方は、輻射によって加熱または冷却されることがあります。CFA モデルにおいて、輻射熱伝達は、輻射輸送方程式 (RTE) を解いてから、総エネルギー保存式の輻射ソース項を取得することによって説明されます。広く使用されているモデリングアプローチである、サーフェス間 (S2S) 輻射モデルが Creo Flow Analysis で選択されているモデルです。
輻射輸送方程式
輻射の光線は、吸収、放射、散乱する媒体層を特定の方向に通過する際に、吸収および光線からの散乱の両方によってエネルギーを失います。さらに、光線は放射および光線への散乱によって媒体内の光源からエネルギーを得ます。媒体の無限層における光線の全体的なエネルギーバランスは、輻射輸送方程式 (RTE) と呼ばれる微分方程式によって表されます。
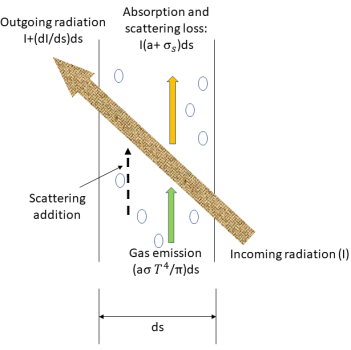
輻射輸送方程式を導くにあたり、図に示すように、強度 I の入射輻射光線が増分厚み ds の媒体 (気体など) を  の方向に通過するものとします。媒体層を通過すると、入射は位置
の方向に通過するものとします。媒体層を通過すると、入射は位置  ⃗ および方向
⃗ および方向  において以下の 4 つの要因によって変化し、輻射強度
において以下の 4 つの要因によって変化し、輻射強度 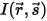 が増すか (エネルギー利得 +) 減少します (エネルギー損失 -)。
が増すか (エネルギー利得 +) 減少します (エネルギー損失 -)。
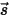 の方向に通過するものとします。媒体層を通過すると、入射は位置
の方向に通過するものとします。媒体層を通過すると、入射は位置 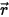 ⃗ および方向
⃗ および方向 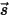 において以下の 4 つの要因によって変化し、輻射強度
において以下の 4 つの要因によって変化し、輻射強度 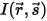 が増すか (エネルギー利得 +) 減少します (エネルギー損失 -)。
が増すか (エネルギー利得 +) 減少します (エネルギー損失 -)。• 吸収 - 気体などの媒体は、そこを通過する輻射の一部を吸収します。吸収係数を 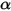 とした場合、吸収によって失われる輻射エネルギーは以下のように表されます。
とした場合、吸収によって失われる輻射エネルギーは以下のように表されます。
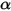 とした場合、吸収によって失われる輻射エネルギーは以下のように表されます。
とした場合、吸収によって失われる輻射エネルギーは以下のように表されます。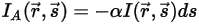
式 2.282
• 散乱 - 気体などの媒体は、光線がその媒体を通過する際、輻射エネルギーの一部を (方向 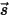 とは) 別の方向に散乱します。散乱係数を
とは) 別の方向に散乱します。散乱係数を 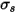 とした場合、散乱によって失われる輻射エネルギーは以下のように表されます。
とした場合、散乱によって失われる輻射エネルギーは以下のように表されます。
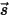 とは) 別の方向に散乱します。散乱係数を
とは) 別の方向に散乱します。散乱係数を 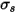 とした場合、散乱によって失われる輻射エネルギーは以下のように表されます。
とした場合、散乱によって失われる輻射エネルギーは以下のように表されます。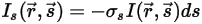
式 2.283
さらに、媒体の屈折率を n とした場合 (指定された媒体における光の速度に対する真空における光の速度の比率として定義)、輻射の光線が得る実際のエネルギーは以下のようになります。
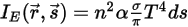
式 2.284
• その他の輻射の散乱 - 媒体の層におけるその他の輻射ソースの一部は、位置および方向ベクトル 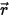 と
と 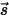 に応じて、輻射の光線内に散乱します。輻射光線の方向と立体角を表す
に応じて、輻射の光線内に散乱します。輻射光線の方向と立体角を表す 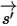
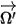 と位相関数
と位相関数 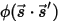 を導入した場合、全方向への光線のうち
を導入した場合、全方向への光線のうち 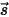 ⃗ の方向に散乱する光線の強度の割合は以下のように表されます。
⃗ の方向に散乱する光線の強度の割合は以下のように表されます。
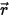 と
と 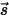 に応じて、輻射の光線内に散乱します。輻射光線の方向と立体角を表す
に応じて、輻射の光線内に散乱します。輻射光線の方向と立体角を表す 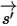
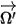 と位相関数
と位相関数 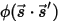 を導入した場合、全方向への光線のうち
を導入した場合、全方向への光線のうち 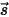 ⃗ の方向に散乱する光線の強度の割合は以下のように表されます。
⃗ の方向に散乱する光線の強度の割合は以下のように表されます。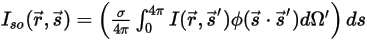
式 2.285
式 2.285では、散乱のプロセスは無視されることに注意してください。
入射輻射を 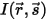 、出射輻射を
、出射輻射を 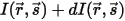 とした場合、方向
とした場合、方向 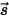 ⃗ における輻射エネルギーのバランスは以下のように表されます。
⃗ における輻射エネルギーのバランスは以下のように表されます。
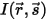 、出射輻射を
、出射輻射を 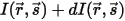 とした場合、方向
とした場合、方向 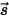 ⃗ における輻射エネルギーのバランスは以下のように表されます。
⃗ における輻射エネルギーのバランスは以下のように表されます。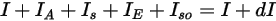
式 2.286
式 2.282から式 2.285を式 2.286に代入して 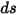 で割ると、以下のような輻射輸送方程式 (RTE) が得られます。
で割ると、以下のような輻射輸送方程式 (RTE) が得られます。
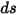 で割ると、以下のような輻射輸送方程式 (RTE) が得られます。
で割ると、以下のような輻射輸送方程式 (RTE) が得られます。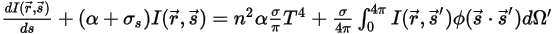
式 2.287
RTE は固定方向 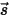 における輻射強度
における輻射強度 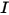 の 1 次微積分方程式です。ドメイン内でこの方程式を解くには、ドメイン内の温度フィールドが必要であり、内部サーフェスと外部サーフェスの両方および 2 つの異なる媒体間の界面における
の 1 次微積分方程式です。ドメイン内でこの方程式を解くには、ドメイン内の温度フィールドが必要であり、内部サーフェスと外部サーフェスの両方および 2 つの異なる媒体間の界面における 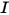 の境界条件も必要です。
の境界条件も必要です。
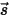 における輻射強度
における輻射強度 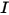 の 1 次微積分方程式です。ドメイン内でこの方程式を解くには、ドメイン内の温度フィールドが必要であり、内部サーフェスと外部サーフェスの両方および 2 つの異なる媒体間の界面における
の 1 次微積分方程式です。ドメイン内でこの方程式を解くには、ドメイン内の温度フィールドが必要であり、内部サーフェスと外部サーフェスの両方および 2 つの異なる媒体間の界面における 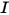 の境界条件も必要です。
の境界条件も必要です。媒体の局所温度は、熱モジュールで説明している、(輻射ソースを含む) 総エネルギー保存式を解くことによって得られます。ただし、熱輻射の場合、境界処理は複雑であり、輻射モデルによって異なります。一般に、境界は放射、反射、吸収する不透過媒体であるか、透過も行う半透過媒体である場合があります。反射と透過には、拡散、鏡面、または拡散と鏡面の両方の場合があります。たとえば、灰色輻射による不透過境界への放射および反射では、反射のタイプに応じて、光線の強度を以下のように表すことができます。
◦ 拡散放射と反射での不透過境界:
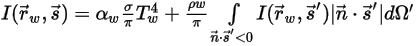
式 2.288
◦ 拡散放射と鏡面反射での不透過境界:
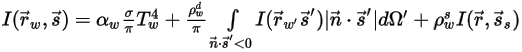
式 2.289
ここで、
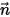 ⃗ ⃗ | 位置 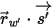 における法線サーフェス方向の単位ベクトル における法線サーフェス方向の単位ベクトル |
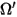 | 拡散反射光線の方向および立体角 (すべての方向で一様な反射) |
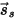 | 鏡面反射光線の方向 (入射に応じた完全な反射) |
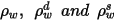 | サーフェス反射率、拡散反射率、および鏡面反射率は、それぞれ以下の関係を持ちます。 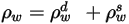 式 2.290 |
与えられた境界条件で、式 2.287は指定された方向における輻射強度の輸送を支配します。灰色輻射の場合、球内のすべての異なる方向で式 2.287を解く必要があります。非灰色輻射の場合、強度は波長にも依存します。したがって、これは波長の全スペクトルにおいてすべての方向で解く必要があります。当然のことながら、輻射輸送方程式を直接解くには非常に時間がかかります。このため、多くのエンジニアリングシミュレーションでは、方向とスペクトルの依存を表すのにある程度簡素化された近似モデルを使用することが推奨されます。CFD のシミュレーションでは、以下の輻射モデルが慣例的に採用されており、その参照に詳細な説明がある場合があります。
参照: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
▪ ロスランド輻射モデル
参照: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ P-1 輻射モデル
参照: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
▪ 離散伝達輻射モデル
参照: N. G. Shah, "A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
参照: M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26. ASME HTD, 1991.
▪ サーフェス間 (S2S) 輻射モデル
参照: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
▪ 離散座標 (DO) 輻射モデル
参照: G. D. Raithby and E. H. Chui, "A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
参照: E. H. Chui and G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method", Numerical Heat Transfer, Part B, 23:269-288, 1993.
各モデルには精度とコストに関して独自の利点と制約があります。たとえば、ロスランドモデルは入射輻射の輸送方程式を解きません。これは最速の輻射モデルであり、必要な追加メモリは最小限で済みます。ロスランドは、輻射輸送方程式を極限まで簡素化したことにより、光学的に厚みのある (光学的厚さとは、媒体内で透過された輻射力に対する入射の輻射力の比の自然対数) 媒体のみに使用できます。
離散座標 (DO) 輻射モデルは式 2.287を空間座標 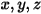 での輻射強度の輸送方程式に変換し、ベクトル方向
での輻射強度の輸送方程式に変換し、ベクトル方向 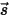 に関連付けられている離散立体角の有限数についてこれを解きます。選択した立体角の数によって、精度と計算コストが直接的に決まります。DO モデリングアプローチは、流体流れおよびエネルギーの式に使用されるアプローチとも同じです。現在のところ、これはすべての光学的厚さを対象とする最も一般的な輻射モデルであり、サーフェス間輻射から燃焼システムなどの関与する輻射まで、広範な問題に適用できます。ただし、非灰色輻射では DO モデルの計算コストは高くなります。
に関連付けられている離散立体角の有限数についてこれを解きます。選択した立体角の数によって、精度と計算コストが直接的に決まります。DO モデリングアプローチは、流体流れおよびエネルギーの式に使用されるアプローチとも同じです。現在のところ、これはすべての光学的厚さを対象とする最も一般的な輻射モデルであり、サーフェス間輻射から燃焼システムなどの関与する輻射まで、広範な問題に適用できます。ただし、非灰色輻射では DO モデルの計算コストは高くなります。
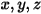 での輻射強度の輸送方程式に変換し、ベクトル方向
での輻射強度の輸送方程式に変換し、ベクトル方向 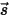 に関連付けられている離散立体角の有限数についてこれを解きます。選択した立体角の数によって、精度と計算コストが直接的に決まります。DO モデリングアプローチは、流体流れおよびエネルギーの式に使用されるアプローチとも同じです。現在のところ、これはすべての光学的厚さを対象とする最も一般的な輻射モデルであり、サーフェス間輻射から燃焼システムなどの関与する輻射まで、広範な問題に適用できます。ただし、非灰色輻射では DO モデルの計算コストは高くなります。
に関連付けられている離散立体角の有限数についてこれを解きます。選択した立体角の数によって、精度と計算コストが直接的に決まります。DO モデリングアプローチは、流体流れおよびエネルギーの式に使用されるアプローチとも同じです。現在のところ、これはすべての光学的厚さを対象とする最も一般的な輻射モデルであり、サーフェス間輻射から燃焼システムなどの関与する輻射まで、広範な問題に適用できます。ただし、非灰色輻射では DO モデルの計算コストは高くなります。前述の輻射モデルのうち、サーフェス間 (S2S) 輻射モデルは、関与する媒体を考慮せずにエンクロージャの輻射輸送をモデリングするのに特に適しています。一般的な例としては、輻射暖房具、自動車のアンダーフードシステム、およびアンターボディシステムなどがあります。これらの状況では、関与する輻射の輻射モデルが効率的でない場合があります。DO 輻射モデルと比べて、S2S モデルはイテレーションあたりの時間は短くなりますが、形態係数の計算そのもので CPU の使用率が高くなることがあります。Creo Flow Analysis では、輻射熱伝達のモデルとして現在のところ S2S 輻射モデルが選択されています。
サーフェス間 (S2S) 輻射モデル
サーフェス間輻射モデルは、関与する媒体なしで灰色の拡散サーフェスから構成されるエンクロージャ内の輻射交換を表します。サーフェス間輻射エネルギー交換が依存する 2 つの主な要素として、関連するサーフェスの輻射特性と、表面積、形状、サーフェス間の相対位置 (分離距離および方向) などのジオメトリパラメータがあります。S2S 輻射モデルでは、サーフェス輻射熱伝達は灰色拡散輻射モデルによって考慮されますが、ジオメトリパラメータは形態係数と呼ばれるジオメトリ関数によって考慮されます。
• 灰色拡散輻射
S2S 輻射モデルでは、灰色の拡散サーフェスである (灰色輻射) を前提としています。灰色サーフェスでは、サーフェスの放射率 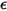 と吸収率
と吸収率 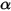 は出射光線および入射光線の波長に依存しません。式 2.274での熱輻射のキルヒホッフの法則によれば、放射率と吸収率は等しくなります。
は出射光線および入射光線の波長に依存しません。式 2.274での熱輻射のキルヒホッフの法則によれば、放射率と吸収率は等しくなります。
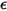 と吸収率
と吸収率 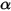 は出射光線および入射光線の波長に依存しません。式 2.274での熱輻射のキルヒホッフの法則によれば、放射率と吸収率は等しくなります。
は出射光線および入射光線の波長に依存しません。式 2.274での熱輻射のキルヒホッフの法則によれば、放射率と吸収率は等しくなります。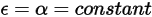
式 2.291
さらに、拡散サーフェスであるという前提により、サーフェス上で鏡面反射が生じることはなく、サーフェスにおける入射輻射の反射率 (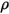 ) は立体角に関してあらゆる方向で等しくなります。式 2.290から、サーフェスの反射率は以下のように計算されます。
) は立体角に関してあらゆる方向で等しくなります。式 2.290から、サーフェスの反射率は以下のように計算されます。
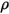 ) は立体角に関してあらゆる方向で等しくなります。式 2.290から、サーフェスの反射率は以下のように計算されます。
) は立体角に関してあらゆる方向で等しくなります。式 2.290から、サーフェスの反射率は以下のように計算されます。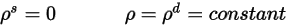
式 2.292
ここで、
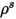 | サーフェス鏡面 |
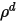 | 拡散反射率 |
非不透過サーフェスまたは半透過サーフェスの場合、透過率 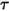 も波長に依存しません。
も波長に依存しません。
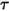 も波長に依存しません。
も波長に依存しません。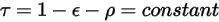
式 2.293
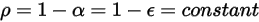
式 2.294
サーフェス灰色拡散輻射の前提により、S2S モデリング式は各サーフェスでのエネルギー保存に基づいて構築されます。
• S2S モデリング式
S2S モデルの主な前提として、閉じたシステムにおいては、輻射熱伝達は灰色拡散サーフェス間でのみ生じます (灰色輻射)。サーフェスを隔てる媒体における輻射の吸収、放射、または拡散は無視できます。したがって、数値解析ではサーフェス間の輻射のみを考慮します。
特定のサーフェスから放出される輻射エネルギー流束は直接放射および反射されるエネルギーから成ります。反射されるエネルギー流束は周囲からの入射エネルギー流束に依存し、これはその他すべてのサーフェスから放出されるエネルギーによって表すことができます。サーフェスにおける正味の輻射エネルギー流れを計算するには、ラジオシティ 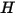 を定義すると便利です。これは、単位面積あたりの放射パワー (発散度)
を定義すると便利です。これは、単位面積あたりの放射パワー (発散度) 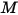 およびサーフェスが受ける単位面積あたりの輻射パワー (放射照度)
およびサーフェスが受ける単位面積あたりの輻射パワー (放射照度) 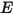 の反射部分を合計したものです。
の反射部分を合計したものです。
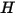 を定義すると便利です。これは、単位面積あたりの放射パワー (発散度)
を定義すると便利です。これは、単位面積あたりの放射パワー (発散度) 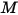 およびサーフェスが受ける単位面積あたりの輻射パワー (放射照度)
およびサーフェスが受ける単位面積あたりの輻射パワー (放射照度) 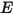 の反射部分を合計したものです。
の反射部分を合計したものです。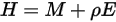
式 2.295
不透過サーフェスの場合、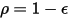 なので、ラジオシティは以下のようになります。
なので、ラジオシティは以下のようになります。
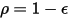 なので、ラジオシティは以下のようになります。
なので、ラジオシティは以下のようになります。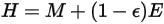
式 2.296
したがって、S2S モデルでの前提により、閉じたシステムにおける各サーフェスでのラジオシティを計算するため、以下の連立一次方程式を構築できます。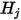 は任意のサーフェス
は任意のサーフェス 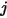 におけるラジオシティを表し、
におけるラジオシティを表し、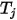 をサーフェス温度、
をサーフェス温度、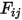 をサーフェス
をサーフェス 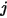 と
と  の間の形態係数とした場合、サーフェス
の間の形態係数とした場合、サーフェス  におけるラジオティは以下のようになります。
におけるラジオティは以下のようになります。
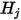 は任意のサーフェス
は任意のサーフェス 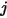 におけるラジオシティを表し、
におけるラジオシティを表し、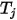 をサーフェス温度、
をサーフェス温度、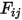 をサーフェス
をサーフェス 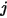 と
と  の間の形態係数とした場合、サーフェス
の間の形態係数とした場合、サーフェス  におけるラジオティは以下のようになります。
におけるラジオティは以下のようになります。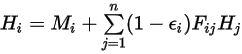
式 2.297
ここで、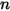 は輻射熱伝達に関与するサーフェスの数です。クロネッカーシンボル
は輻射熱伝達に関与するサーフェスの数です。クロネッカーシンボル 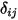 を導入し、灰色輻射のシュテファン-ボルツマンの法則式 2.278を適用することで、式 2.297を再編成して以下のような S2S モデリング式を導くことができます。
を導入し、灰色輻射のシュテファン-ボルツマンの法則式 2.278を適用することで、式 2.297を再編成して以下のような S2S モデリング式を導くことができます。
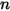 は輻射熱伝達に関与するサーフェスの数です。クロネッカーシンボル
は輻射熱伝達に関与するサーフェスの数です。クロネッカーシンボル 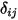 を導入し、灰色輻射のシュテファン-ボルツマンの法則式 2.278を適用することで、式 2.297を再編成して以下のような S2S モデリング式を導くことができます。
を導入し、灰色輻射のシュテファン-ボルツマンの法則式 2.278を適用することで、式 2.297を再編成して以下のような S2S モデリング式を導くことができます。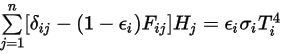
式 2.298
事前に計算された形態係数 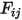 を使用して式 2.298の連立一次方程式を解き、関与するサーフェスの
を使用して式 2.298の連立一次方程式を解き、関与するサーフェスの 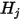 を取得します。これにより、各サーフェス上の輻射の正味の熱流が簡単に計算されます。サーフェス
を取得します。これにより、各サーフェス上の輻射の正味の熱流が簡単に計算されます。サーフェス  では、単位面積あたりの出射 (
では、単位面積あたりの出射 (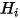 ) 輻射と入射 (
) 輻射と入射 (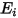 ) 輻射の差が正味の輻射熱流束
) 輻射の差が正味の輻射熱流束 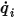 になります。式 2.278および式 2.296から、以下の流束の式を導くことができます。
になります。式 2.278および式 2.296から、以下の流束の式を導くことができます。
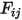 を使用して式 2.298の連立一次方程式を解き、関与するサーフェスの
を使用して式 2.298の連立一次方程式を解き、関与するサーフェスの 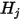 を取得します。これにより、各サーフェス上の輻射の正味の熱流が簡単に計算されます。サーフェス
を取得します。これにより、各サーフェス上の輻射の正味の熱流が簡単に計算されます。サーフェス  では、単位面積あたりの出射 (
では、単位面積あたりの出射 (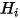 ) 輻射と入射 (
) 輻射と入射 (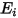 ) 輻射の差が正味の輻射熱流束
) 輻射の差が正味の輻射熱流束 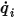 になります。式 2.278および式 2.296から、以下の流束の式を導くことができます。
になります。式 2.278および式 2.296から、以下の流束の式を導くことができます。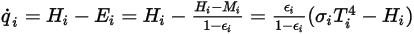
式 2.299
与えられた表面積 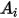 で、サーフェスから放出される正味の輻射熱フロー
で、サーフェスから放出される正味の輻射熱フロー 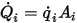 は以下のように計算されます。
は以下のように計算されます。
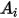 で、サーフェスから放出される正味の輻射熱フロー
で、サーフェスから放出される正味の輻射熱フロー 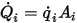 は以下のように計算されます。
は以下のように計算されます。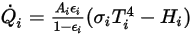
式 2.300
S2S モデルは式 2.298の形式による連立一次方程式から成ります。このモデルを適用する利点として、与えられた形態係数と温度で、連立一次方程式を解くことによって正味の熱流を計算でき、これは数値アルゴリズムを適用することによって計算されます。ただし、提案されたサーフェス間モデルを適用する際の主な問題として、関与する n 個のサーフェスの 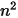 個の形態係数の計算が挙げられます。サーフェスの数が増えた場合には特に、これには時間がかかることがあります。
個の形態係数の計算が挙げられます。サーフェスの数が増えた場合には特に、これには時間がかかることがあります。
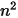 個の形態係数の計算が挙げられます。サーフェスの数が増えた場合には特に、これには時間がかかることがあります。
個の形態係数の計算が挙げられます。サーフェスの数が増えた場合には特に、これには時間がかかることがあります。形態係数の計算
S2S モデリングの式 2.298において、形態係数 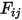 はサーフェス
はサーフェス  から放出される輻射とサーフェス
から放出される輻射とサーフェス 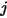 に当たる輻射の比率です。図 2.37に示すように、
に当たる輻射の比率です。図 2.37に示すように、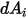 をサーフェス
をサーフェス  上の微分領域、
上の微分領域、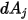 をサーフェス
をサーフェス 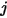 上の微分領域、
上の微分領域、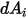 と
と 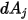 の間の距離を
の間の距離を 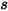 とした場合、距離
とした場合、距離 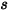 における
における 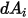 から
から 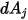 までの形態係数
までの形態係数 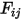 は以下のように表されます。
は以下のように表されます。
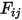 はサーフェス
はサーフェス  から放出される輻射とサーフェス
から放出される輻射とサーフェス 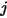 に当たる輻射の比率です。図 2.37に示すように、
に当たる輻射の比率です。図 2.37に示すように、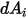 をサーフェス
をサーフェス  上の微分領域、
上の微分領域、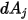 をサーフェス
をサーフェス 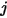 上の微分領域、
上の微分領域、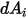 と
と 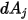 の間の距離を
の間の距離を 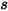 とした場合、距離
とした場合、距離 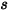 における
における 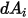 から
から 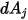 までの形態係数
までの形態係数 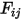 は以下のように表されます。
は以下のように表されます。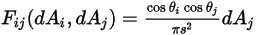
式 2.301
ここで、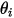 と
と 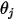 は、2 つの微小領域間の光線とサーフェス法線方向の間の角度です。
は、2 つの微小領域間の光線とサーフェス法線方向の間の角度です。
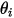 と
と 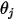 は、2 つの微小領域間の光線とサーフェス法線方向の間の角度です。
は、2 つの微小領域間の光線とサーフェス法線方向の間の角度です。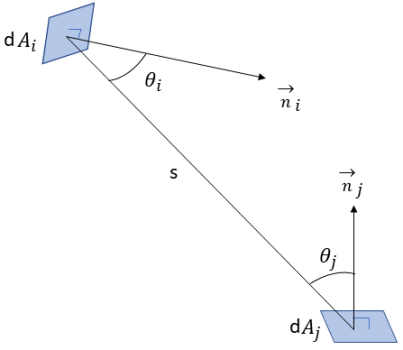
図 2.37
 および
および 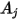 がそれぞれサーフェス
がそれぞれサーフェス  および
および 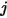 の与えられた面積である場合、サーフェス
の与えられた面積である場合、サーフェス  からサーフェス
からサーフェス 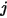 までの形態係数は式 2.301をサーフェス
までの形態係数は式 2.301をサーフェス  および
および 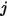 について積分したものの面積平均になります。
について積分したものの面積平均になります。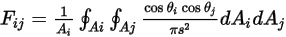
式 2.302
2 つのサーフェスが相互に可視である、つまり形態係数がゼロ以外である場合にのみ、サーフェス間輻射が生じることに注意してください。 と
と  の間の可視状態についてクロネッカーシンボル
の間の可視状態についてクロネッカーシンボル  を導入すると、以下のようになります。
を導入すると、以下のようになります。
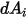 と
と 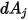 の間の可視状態についてクロネッカーシンボル
の間の可視状態についてクロネッカーシンボル 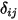 を導入すると、以下のようになります。
を導入すると、以下のようになります。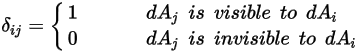
式 2.303
式 2.302を以下のように書き直すことができます。
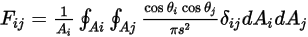
式 2.304
互いに可視である任意の 2 つのサーフェスにおいて、図 2.378に示すように、サーフェス  は出射輻射エネルギーの一部だけをサーフェス
は出射輻射エネルギーの一部だけをサーフェス 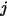 に対して輻射します。したがって、無次元形態係数
に対して輻射します。したがって、無次元形態係数 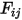 は、サーフェス
は、サーフェス  から放出されてサーフェス
から放出されてサーフェス 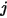 に達するエネルギーの割合を表します。特性は後続のリストにあります。
に達するエネルギーの割合を表します。特性は後続のリストにあります。
 は出射輻射エネルギーの一部だけをサーフェス
は出射輻射エネルギーの一部だけをサーフェス  に対して輻射します。したがって、無次元形態係数
に対して輻射します。したがって、無次元形態係数 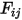 は、サーフェス
は、サーフェス  から放出されてサーフェス
から放出されてサーフェス  に達するエネルギーの割合を表します。特性は後続のリストにあります。
に達するエネルギーの割合を表します。特性は後続のリストにあります。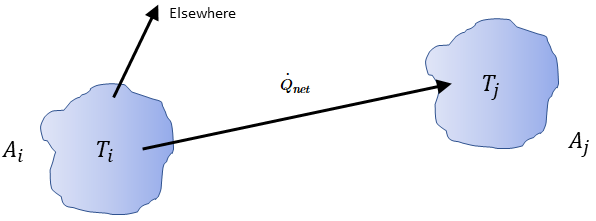
図 2.378
• 形態係数の総和 - サーフェスから放出される輻射は保存されるので、任意のサーフェス  からのすべての形態係数の合計は 1 になります。
からのすべての形態係数の合計は 1 になります。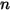 サーフェスの閉じたシステムでは、以下のようになります。
サーフェスの閉じたシステムでは、以下のようになります。
 からのすべての形態係数の合計は 1 になります。
からのすべての形態係数の合計は 1 になります。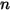 サーフェスの閉じたシステムでは、以下のようになります。
サーフェスの閉じたシステムでは、以下のようになります。
式 2.305
• 自己可視サーフェス - 輻射は直線移動するので、凸状サーフェスからの輻射光線はサーフェスから放出されず、後から同じサーフェスに当たります。したがって、凸状サーフェスは自己不可視です。
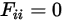
式 2.306
凹状サーフェスの場合、サーフェス上のある位置からの出射光線は同じサーフェス上の別の位置に後で当たります。したがって、凹状サーフェスは自己可視です。
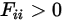
式 2.307
• 重ね合わせ - 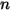 サーフェスシステムの場合、あるサーフェス
サーフェスシステムの場合、あるサーフェス  が
が 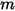 個のサーフェス (
個のサーフェス (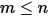 ) に輻射する場合、サーフェス
) に輻射する場合、サーフェス  と
と 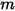 個のサーフェスの間の形態係数は、サーフェス
個のサーフェスの間の形態係数は、サーフェス  と
と 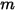 個の各サーフェスとの間の形態係数の合計と等しくなります。
個の各サーフェスとの間の形態係数の合計と等しくなります。
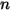 サーフェスシステムの場合、あるサーフェス
サーフェスシステムの場合、あるサーフェス  が
が 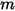 個のサーフェス (
個のサーフェス (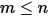 ) に輻射する場合、サーフェス
) に輻射する場合、サーフェス  と
と 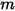 個のサーフェスの間の形態係数は、サーフェス
個のサーフェスの間の形態係数は、サーフェス  と
と 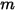 個の各サーフェスとの間の形態係数の合計と等しくなります。
個の各サーフェスとの間の形態係数の合計と等しくなります。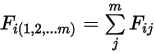
式 2.308
重ね合わせの規則や総和規則は特定のチャートまたはグラフでジオメトリを表すことができない場合に便利です。重ね合わせの規則によって、既知のジオメトリの和または差を使用して調査対象のジオメトリを表すことができます。
• 相反定理 - 式 2.304では、形態係数 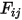 が、サーフェス
が、サーフェス  から放出されてサーフェス
から放出されてサーフェス 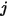 に達する輻射エネルギーの割合として定義されています。同様に、サーフェス
に達する輻射エネルギーの割合として定義されています。同様に、サーフェス 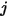 から放出されてサーフェス
から放出されてサーフェス  に達するエネルギーの割合である形態係数
に達するエネルギーの割合である形態係数 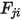 は以下のように表されます。
は以下のように表されます。
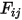 が、サーフェス
が、サーフェス  から放出されてサーフェス
から放出されてサーフェス 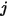 に達する輻射エネルギーの割合として定義されています。同様に、サーフェス
に達する輻射エネルギーの割合として定義されています。同様に、サーフェス 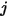 から放出されてサーフェス
から放出されてサーフェス  に達するエネルギーの割合である形態係数
に達するエネルギーの割合である形態係数 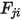 は以下のように表されます。
は以下のように表されます。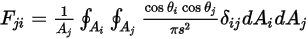
式 2.309
式 2.309を式 2.304と比較した場合、以下の関係が得られます。
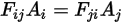
式 2.310
式 2.310は形態係数の相反定理と呼ばれます。この相反定理によって、形態係数のペアのいずれか 1 つだけを直接計算すればよくなります。
クラスタ
輻射サーフェスの数が多い場合、S2S 輻射モデルの計算コストは高くなります。計算時間とストレージ要件を削減するため、一定数の隣接する境界-セル面をグループ化してサーフェスクラスタを作成することによって、輻射サーフェスの数を減らすことができます。これにより、サーフェスクラスタについてラジオシティ ( ) が計算されます。これらの値が各クラスタ内の境界-セル面に分配されて壁温度が計算されます。輻射のソース項は非線形性が非常に高いので (温度の 4 乗に比例)、サーフェスクラスタの平均温度を計算し、クラスタを構成する境界面間に流束およびソース項を適切に分配するようにします。
) が計算されます。これらの値が各クラスタ内の境界-セル面に分配されて壁温度が計算されます。輻射のソース項は非線形性が非常に高いので (温度の 4 乗に比例)、サーフェスクラスタの平均温度を計算し、クラスタを構成する境界面間に流束およびソース項を適切に分配するようにします。
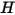 ) が計算されます。これらの値が各クラスタ内の境界-セル面に分配されて壁温度が計算されます。輻射のソース項は非線形性が非常に高いので (温度の 4 乗に比例)、サーフェスクラスタの平均温度を計算し、クラスタを構成する境界面間に流束およびソース項を適切に分配するようにします。
) が計算されます。これらの値が各クラスタ内の境界-セル面に分配されて壁温度が計算されます。輻射のソース項は非線形性が非常に高いので (温度の 4 乗に比例)、サーフェスクラスタの平均温度を計算し、クラスタを構成する境界面間に流束およびソース項を適切に分配するようにします。サーフェスクラスタの温度は、以下の式に示すように境界面温度の面積平均によって得られます。
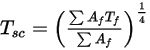
式 2.311
ここで、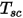 はサーフェスクラスタの温度、
はサーフェスクラスタの温度、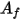 は CFA シミュレーションにおける境界セルの面の面積、
は CFA シミュレーションにおける境界セルの面の面積、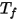 はその温度です。総和はサーフェスクラスタ内のすべての面について行われます。
はその温度です。総和はサーフェスクラスタ内のすべての面について行われます。
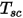 はサーフェスクラスタの温度、
はサーフェスクラスタの温度、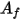 は CFA シミュレーションにおける境界セルの面の面積、
は CFA シミュレーションにおける境界セルの面の面積、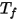 はその温度です。総和はサーフェスクラスタ内のすべての面について行われます。
はその温度です。総和はサーフェスクラスタ内のすべての面について行われます。 ) および光線への放射特性に従って、灰色体として光線に輻射エネルギーを放射します。シュテファン-ボルツマンの法則および放射と吸収との間の相反定理、
) および光線への放射特性に従って、灰色体として光線に輻射エネルギーを放射します。シュテファン-ボルツマンの法則および放射と吸収との間の相反定理、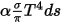
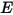 がサーフェス上の単位面積あたりに入射する場合 (放射照度)、反射、吸収、および透過される輻射エネルギーの部分は、それぞれ
がサーフェス上の単位面積あたりに入射する場合 (放射照度)、反射、吸収、および透過される輻射エネルギーの部分は、それぞれ 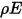 、
、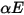 、および
、および 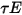 になります。ほとんどの用途では、サーフェスは赤外線スペクトルの熱輻射を通さないので、輻射サーフェスをさらに不透過と見なすことができます。したがって、透過率は無視できます
になります。ほとんどの用途では、サーフェスは赤外線スペクトルの熱輻射を通さないので、輻射サーフェスをさらに不透過と見なすことができます。したがって、透過率は無視できます 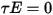 。
。 は以下のように表されます。
は以下のように表されます。