定義
• 共振周波数 - 1 秒あたりに発生する運動サイクル数。ばね定数 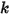 と質量
と質量 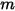 を使用して計算されます。
を使用して計算されます。
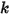 と質量
と質量 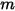 を使用して計算されます。
を使用して計算されます。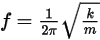
ここで、
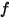 | 共振周波数 (Hz) |
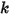 | ばね定数 |
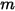 | 質量 (kg) |
• ゼロ変位 - モデルセットアップ中のダイナミック境界の位置。セットアップ位置からのオフセットを含む場合があるため、変位がゼロの場合、ダイナミック境界がセットアップ位置とは一致しなくなります。
• 変位 (m) - 直線移動 (1DOF) の ODE でのゼロ変位位置を基準にしたダイナミック境界の線形直線移動のマグニチュード。指定運動条件では、変位が指定変位に一致します。
• 速度 (m) - 直線移動 (1DOF) の ODE でのダイナミック境界の速度のマグニチュード。正の速度の方向は、運動の方向と同一です。指定運動では、速度が指定変位の時間微分に一致します。
• 加速度 (m/s2) - ダイナミック境界の加速度のマグニチュード。指定運動では、加速度が指定変位に対する速度の時間微分に一致します。
• 減衰力 (N) - 振動するボディの動きを制御する力。たとえば、ばねでは空気が減衰媒体の役割を果たします。正の減衰力の方向は、運動の方向と同一です。
• ばね定数 - フォースバランス方程式でのばねフォースの変数。ばね定数に関連付けられたばねフォースは、変位の増加に逆らいます。
• ばねフォース (N) - 初期荷重フォース、ばね定数、変位に基づきます。正のばねフォースの方向は、運動の方向と同一です。
• ばね初期荷重フォース (N) - 変位がゼロ変位に等しいときのばねの力。ゼロ変位は、初期変位と同一ではありません。このフォースに関連付けられたばねフォースは、変位の増加に逆らいます。
• 流体力 (N) - 圧力とせん断力を含むこの流体力学上の力。正の流体力の方向は、運動の方向と同一です。
• 摩擦フォース (N) - 接触フォースと摩擦係数の法線成分。
• ネットフォース (N) - 流体力、減衰力、ばね初期荷重フォースおよびばね定数 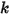 に起因するばねフォース、接触摩擦、その他のボディにかかる力などのフォースの寄与。正のネットフォースの方向は、運動の方向と同一です。
に起因するばねフォース、接触摩擦、その他のボディにかかる力などのフォースの寄与。正のネットフォースの方向は、運動の方向と同一です。
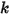 に起因するばねフォース、接触摩擦、その他のボディにかかる力などのフォースの寄与。正のネットフォースの方向は、運動の方向と同一です。
に起因するばねフォース、接触摩擦、その他のボディにかかる力などのフォースの寄与。正のネットフォースの方向は、運動の方向と同一です。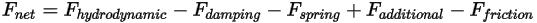
ここで、
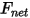 | ネットフォース (N) |
 | 流体力 (N) |
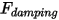 | 減衰力 (N) |
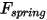 | ばねフォース (N) |
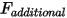 | その他のフォース (N) |
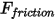 | せん断力 (N) |
• ゼロ角度変位 - モデルセットアップ中のダイナミック境界の位置。セットアップ位置からのオフセットを含む場合があるため、変位がゼロの場合、ダイナミック境界がセットアップ位置とは一致しなくなります。
• 角度変位 (deg) -ゼロ角度変位の位置を基準にしたダイナミック境界の回転のマグニチュード。回転の角度および正方向は回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、角度は反時計回りの方向に増加します。指定運動では、角変位が指定角変位に一致します。
• 角速度 (rad/s) - ダイナミック境界の角速度のマグニチュード。角速度の符号は、回転 (1 DOF) モジュールに対する回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、正の角速度は反時計回りに生じます。指定運動では、角速度が rad/s に変換された指定角の時間微分に一致します。
• 角加速度 (rad/s2) - 回転 (1 自由度) の ODE でのゼロ角変位位置を基準にしたダイナミック境界の回転のマグニチュード。加速度の角度および正方向は回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、角度は反時計回りの方向に増加します。指定運動では、角加速度が指定角変位に基づく角速度の変化に対応します。
• 減衰トルク (N-m) - 角速度と減衰係数に基づきます。減衰トルクの符号は、回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、正の減衰トルクは反時計回りに生じます。
• 流体トルク (N-m) - 流体力学上のトルク。流体トルクの符号は、回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、正の流体トルクは反時計回りに生じます。
• ばねトルク (N-m) - 変位角、ねじれ初期荷重トルク、ねじれ定数に基づきます。ばねトルクの符号は、回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、正のばねトルクは反時計回りに生じます。
• 制動トルク (N-m) - 減衰による制動トルク。回転速度 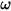 とユーザー定義の減衰係数に依存します。
とユーザー定義の減衰係数に依存します。
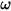 とユーザー定義の減衰係数に依存します。
とユーザー定義の減衰係数に依存します。• ネットトルク (N-m) - 流体トルク、減衰力、ねじれ初期荷重トルクおよびねじれ定数に起因するばねトルク、その他のトルクならびに接触摩擦などのトルクの寄与。ネットトルクの符号は、回転軸ベクトルと右手の法則に基づきます。このため、軸がオブザーバーを指している場合、正のネットトルクは反時計回りに生じます。
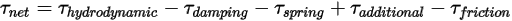
ここで、
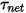 | ネットトルク (N-m) |
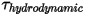 | 流体トルク (N-m) |
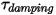 | 減衰トルク (N-m) |
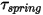 | ばねトルク (N-m) |
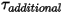 | その他のトルク (N-m) |
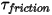 | せん断トルク (N-m) |