Teoria dei modelli di cavitazione
Nell'equazione 2.169 di trasporto vapore, Re e Rc sono i termini di origine di trasferimento di massa collegati allo sviluppo e alla compressione delle bolle di vapore nei flussi di cavitazione. Tali termini indicano lo scambio di massa tra le fasi vapore e liquido durante un processo di cavitazione. Re e Rc sono modellati sull'equazione di Rayleigh-Plesset che descrive lo sviluppo di una singola bolla di vapore in un liquido.
Trasferimento di massa liquido-vapore
Per derivare un'espressione della frequenza di modifica della fase netta nel processo di cavitazione, considerate un flusso bifase liquido-vapore incomprimibile con velocità di slittamento pari a zero in cui il gas non condensabile non viene considerato. Se introducete R per rappresentare la velocità netta del trasferimento di massa da liquido a vapore, avrete le equazioni della frazione di volume di liquido e vapore e l'equazione di continuità della massa totale come riportato di seguito.
• Fase liquida
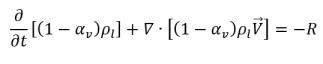
equazione 2.179
• Fase vapore
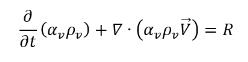
equazione 2.180
• Miscela (continuità di massa totale)
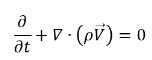
equazione 2.181
Nel sistema bifase liquido-vapore, la densità della miscela ρ viene espressa in funzione della densità della frazione di volume vapore e della densità di fase:
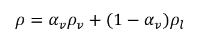
equazione 2.182
Poiché si presume che sia la densità del liquido che quella del vapore sono costanti (incomprimibili), una relazione tra il gradiente di velocità e la frazione di volume vapore viene derivata dall'equazione 2.181 e dall'equazione 2.182:
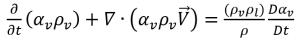
equazione 2.183
Combinando l'equazione 2.179 e l'equazione 2.183 si avrà l'espressione per il termine di origine della massa netta, ovvero:
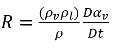
equazione 2.184
Sostituendo l'equazione 2.184 nell'equazione 2.180, l'equazione della frazione di volume vapore può essere riscritta nella forma generale:
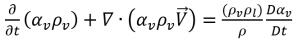
equazione 2.185
Applicando la relazione tra la frazione di massa e la frazione di volume dell'equazione 2.173, avrete l'equazione 2.185 in funzione della frazione di massa vapore:
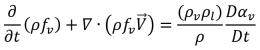
equazione 2.186
Dall'equazione 2.185 ed equazione 2.186, risulta chiaro che, con velocità di slittamento pari a zero tra la fase liquida e la fase vapore, la cavitazione può essere modellata come flusso monofase con una equazione di trasporto della frazione di massa vapore aggiuntiva o come flusso della miscela multifase euleriana con il trasferimento di massa liquido-vapore. Senza considerare l'effetto della diffusione e la differenza di velocità tra le fasi, i due approcci dal punto di vista matematico sono identici. Per modellare i flussi di cavitazione, Creo Flow Analysis utilizza l'approccio monofase.
Considerazione dinamiche sulle bolle
Per la maggior parte degli eventi naturali e dei sistemi di progettazione tecnica per l'inizio del processo di cavitazione, esiste un numero adeguato di nuclei come bolle, gas non condensabili e così via. Per modellare il processo di cavitazione, di conseguenza, è necessario tenere in considerazione lo sviluppo e la compressione delle bolle. Se si assume che in un liquido fluttuante la velocità di slittamento tra le bolle del liquido e le bolle di vapore è uguale a zero, l'equazione dinamica delle bolle deriva dall'equazione di Rayleigh-Plesset generalizzata che descrive lo sviluppo di una bolla di gas in un liquido:
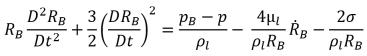
equazione 2.187
dove
RB | raggio della bolla |
pB | pressione nella bolla (presupponendo che sia la pressione del vapore alla temperatura del liquido in assenza di altri gas) |
p | pressione del liquido che circonda la bolla |
σ | coefficiente di tensione superficiale tra il liquido e il vapore |
Questa equazione è derivata dal bilanciamento meccanico (nessuna barriera termica per lo sviluppo della bolla).
Se trascurate la derivata temporale di secondo grado (adatta a frequenze di oscillazione inferiori), il termine di smorzamento viscoso e la forza di tensione superficiale, avrete un'espressione ridotta dell'equazione 2.187 valida per lo stato asintotico:
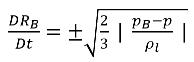
equazione 2.188
Questa equazione di Rayleigh-Plesset ridotta fornisce un approccio fisico per introdurre gli effetti della dinamica delle bolle nei modelli di cavitazione. Il raggio della bolla può aumentare o diminuire in base ai segni di (pB–p): la bolla si sviluppa se p<pB e si comprime se p>pB. Pertanto, l'equazione 2.188 viene riscritta come segue:
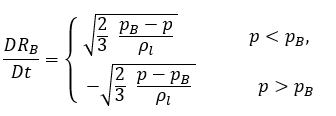
equazione 2.189
Se η è la densità del numero di bolle di vapore in un liquido (il numero di bolle presenti per volume unitario) e tutte le bolle di vapore sono sfere perfette con lo stesso raggio RB, allora la frazione di volume di fase vapore sarà:
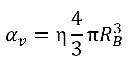
equazione 2.190
Il presupposto è che in un liquido non sia possibile creare o distruggere bolle di vapore, ma le bolle possono svilupparsi (evaporazione) e comprimersi (condensazione) durante il processo di cavitazione. Nell'equazione 2.190, la densità del numero di bolle di vapore (η) rimane costante, ma il raggio della bolla (RB) può aumentare o diminuire. Quindi, la derivata temporale della frazione di volume vapore viene calcolata come:
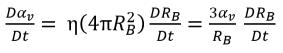
equazione 2.191
Sostituendo l'equazione 2.191 nell'equazione 2.186 l'equazione di trasporto governerà la frazione di massa della fase vapore:
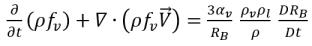
equazione 2.192
Applicando l'equazione 2.189, la velocità netta del trasferimento di massa per volume unitario tra il liquido e il vapore ha la seguente forma:
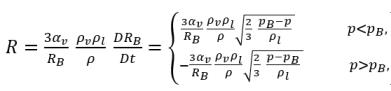
equazione 2.193
dove l'equazione 2.193 indica che nella cavitazione, la velocità di trasferimento della massa del volume unitario (R) è funzione della (proporzionale alla) densità sia della fase vapore che della fase liquida ed è inversamente proporzionale alla densità della miscela. Poiché l'equazione 2.192 è derivata direttamente dalla continuità di fase e dalla continuità di massa della miscela, è esatta e deve rappresentare con precisione il trasferimento di massa tra la fase liquida e la fase vapore nella cavitazione. Con l'introduzione della dinamica delle bolle, l'equazione 2.193 utilizza l'approccio simile per modellare i due processi di trasferimento di massa opposti e fisicamente diversi: da liquido a vapore (sviluppo delle bolle o evaporazione) e da vapore a liquido (compressione delle bolle o condensazione). Per l'equazione 2.192 di trasporto della frazione di massa del vapore, lo sviluppo delle bolle è un termine di origine, mentre la compressione delle bolle viene trattata come termine crescita della bolla è un formato originale, mentre la compressione di bolla viene trattato come termine di risucchio.
Nei modelli pratici di cavitazione, la pressione della zona in condizioni di quiete locale p viene di solito presa in modo che sia uguale alla pressione al centro della cella. La pressione delle bolle pB è uguale alla pressione del vapore di saturazione (psat, una proprietà materiale) in assenza di gas disciolti, trasporto di massa e smorzamento viscoso, pB=psat
Confrontando l'equazione 2.192 e l'equazione 2.193 con l'equazione 2.169 della frazione della massa di vapore, i termini di origine Re e Rc sono i seguenti:
• Se la pressione del flusso locale è inferiore alla pressione del vapore di saturazione, p<psat, si verifica soltanto l'evaporazione:
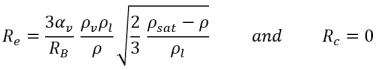
equazione 2.194
• Se la pressione del flusso locale è superiore alla pressione del vapore di saturazione, p>psat, si verifica soltanto la condensazione:
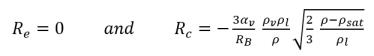
equazione 2.195
L'equazione 2.194 e l'equazione 2.195 sono alla di quasi tutti i modelli di cavitazione bifase meccanici disponibili. Creo Flow Analysis ha utilizzato l'approccio di modellazione di Singhal et al.
Assorbimento/discioglimento ed emissione di gas
I gas non condensabili sono spesso presenti in un fluido di lavoro e possono avere un impatto significativo sulla cavitazione. A volte un gas non condensabile si sposta liberamente con il flusso e si dissolve o viene emesso da un liquido, puntando naturalmente verso un equilibrio dinamico delle concentrazioni di massa tra le fasi liquida e gassosa. L'assorbimento o il discioglimento del gas e l'emissione in un liquido sono un fenomeno di trasferimento di massa liquido-gas che dipende dalle differenze delle concentrazioni delle masse e dai gradienti. Per modellare i flussi di cavitazione è necessario tenere in considerazione anche l'effetto del gas non condensabile e il possibile trasferimento della massa liquido-gas nel flusso della miscela.
Presupponendo che in un flusso bifase liquido-gas, un gas non condensabile come aria oppure ossigeno, esiste sia nella fase liquida (gas disciolto) che nella fase gassosa (gas libero), le equazioni di trasferimento della frazione di massa di gas sono riportate di seguito.
• Gas libero (fase gassosa)
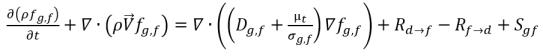
equazione 2.196
• Gas disciolto (fase liquida)
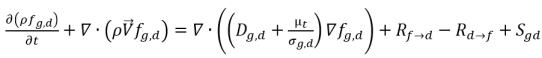
equazione 2.197
dove
fg,f | frazioni di massa del gas libero |
fg,d | frazioni di massa del gas libero e del gas disciolto, |
Sg,f, Sg,d | origini esterne o definite dall'utente |
Dg,f | diffusività del gas libero e del gas disciolto |
Dg,d | diffusività del gas disciolto |
Se la frazione di massa di un gas non condensabile viene predescritta come fg, allora avrete:
fg=fg,f
o il suo trasporto nello spazio e nel tempo può essere ottenuto risolvendo l'equazione di seguito.
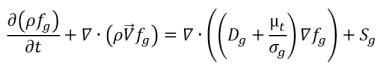
equazione 2.199
Notate che solo due tra l'equazione 2.196, l'equazione 2.197 e l'equazione 2.199 possono essere risolte direttamente.
Nell'equazione 2.196 e nell'equazione 2.197, l'origine Rd→f indica la velocità di emissione del gas disciolto e Rf→d indica la velocità di assorbimento o di discioglimento del gas libero.
Quando le due fasi sono a contatto, vi è una tendenza per il gas libero f e il gas disciolto d trasportati da una fase all'altra a raggiungere un equilibrio dinamico tra le due fasi. I modelli di equilibrio presuppongono che le velocità volumetriche dei trasferimenti di massa dipendono dai gradienti o dalle differenze di concentrazione delle masse:
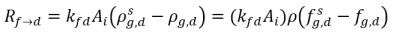
equazione 2.200
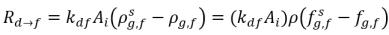
equazione 2.201
dove
AI | area interfacciale liquido-gas |
kf,d(=kd,f) | coefficiente di trasferimento di massa volumetrico in serie |
ρg,d(=ρfg,d) | concentrazioni di massa locali di gas disciolto |
ρg,f(=ρfg,f) | concentrazioni di massa locali di gas libero |
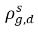 | concentrazioni di massa in equilibrio del gas disciolto nelle fasi di hosting |
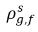 | concentrazioni di massa in equilibrio del gas libero nelle fasi di hosting |
Tenete presente che 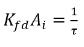 ha l'unità di tempo inverso, 1/s, un indicatore dell'efficienza di trasferimento di massa. L'equazione 2.200 e l'equazione 2.201 hanno anche i seguenti formati:
ha l'unità di tempo inverso, 1/s, un indicatore dell'efficienza di trasferimento di massa. L'equazione 2.200 e l'equazione 2.201 hanno anche i seguenti formati:
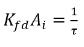 ha l'unità di tempo inverso, 1/s, un indicatore dell'efficienza di trasferimento di massa. L'equazione 2.200 e l'equazione 2.201 hanno anche i seguenti formati:
ha l'unità di tempo inverso, 1/s, un indicatore dell'efficienza di trasferimento di massa. L'equazione 2.200 e l'equazione 2.201 hanno anche i seguenti formati: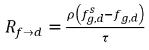
equazione 2.202
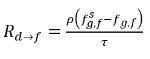
equazione 2.203
Di solito, 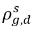 e
e 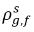 non sono uguali (discontinuità). Esiste una curva di equilibrio ben definita tra le due concentrazioni che dipende dalla temperatura, dalla pressione e dalle composizioni della miscela. La curva di solito è monotona e non lineare ed è spesso espressa come relazione quasi lineare con il coefficiente
non sono uguali (discontinuità). Esiste una curva di equilibrio ben definita tra le due concentrazioni che dipende dalla temperatura, dalla pressione e dalle composizioni della miscela. La curva di solito è monotona e non lineare ed è spesso espressa come relazione quasi lineare con il coefficiente 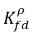
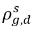 e
e 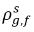 non sono uguali (discontinuità). Esiste una curva di equilibrio ben definita tra le due concentrazioni che dipende dalla temperatura, dalla pressione e dalle composizioni della miscela. La curva di solito è monotona e non lineare ed è spesso espressa come relazione quasi lineare con il coefficiente
non sono uguali (discontinuità). Esiste una curva di equilibrio ben definita tra le due concentrazioni che dipende dalla temperatura, dalla pressione e dalle composizioni della miscela. La curva di solito è monotona e non lineare ed è spesso espressa come relazione quasi lineare con il coefficiente 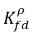
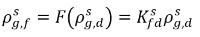
equazione 2.204
dove Kf,d viene deciso utilizzando le leggi fisiche o le correlazioni empiriche. Un approccio comune è seguire la legge di Henry che fornisce una relazione di equilibrio generalizzata. Tale legge definisce che per una miscela liquida a contatto con la fase gassosa, la pressione parziale del gas libero pg,f è uguale al prodotto della frazione molare di equilibrio del gas disciolto nella la fase liquida 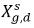 e la costante di Henry, Hx:
e la costante di Henry, Hx:
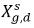 e la costante di Henry, Hx:
e la costante di Henry, Hx: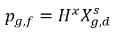
equazione 2.205
Se la fase del gas libero segue la legge del gas ideale, allora la legge di Dalton relativa alla pressione parziale fornisce la seguente equazione:
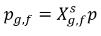
equazione 2.206
Usando equazione 2.204 - equazione 2.206, viene generato il seguente rapporto di equilibrio:
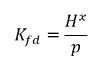
equazione 2.207
Quindi, la costante di Henry ha un'unità di pressione e può essere considerata come pressione di riferimento. Assumendo che, per una miscela liquida ideale a contatto con un gas, la costante di Henry è la pressione del vapore di saturazione psat, l'equazione 2.207 è anche:
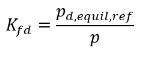
equazione 2.208
dove pd,equil,ref è la pressione di riferimento per la frazione di massa in equilibrio disciolta. Quindi, l'equazione 2.204 può essere riscritta come segue:
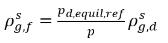
equazione 2.209
Nell'equazione 2.202 e nell'equazione 2.203, 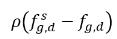 e
e 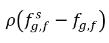 sono le differenze/i gradienti della concentrazione di massa, le forze che consentono l'assorbimento o il discioglimento e l'emissione dei gas non condensabili. Indica che il trasporto del gas non condensabile tra le due fasi richiede una partenza di concentrazione di massa dal suo stato di equilibrio. La direzione del trasferimento di massa sposta il sistema verso equilibrio in base alle concentrazioni di massa locale e in equilibrio in entrambe le fasi. Dal modello di equilibrio si avrà:
sono le differenze/i gradienti della concentrazione di massa, le forze che consentono l'assorbimento o il discioglimento e l'emissione dei gas non condensabili. Indica che il trasporto del gas non condensabile tra le due fasi richiede una partenza di concentrazione di massa dal suo stato di equilibrio. La direzione del trasferimento di massa sposta il sistema verso equilibrio in base alle concentrazioni di massa locale e in equilibrio in entrambe le fasi. Dal modello di equilibrio si avrà:
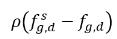 e
e 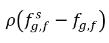 sono le differenze/i gradienti della concentrazione di massa, le forze che consentono l'assorbimento o il discioglimento e l'emissione dei gas non condensabili. Indica che il trasporto del gas non condensabile tra le due fasi richiede una partenza di concentrazione di massa dal suo stato di equilibrio. La direzione del trasferimento di massa sposta il sistema verso equilibrio in base alle concentrazioni di massa locale e in equilibrio in entrambe le fasi. Dal modello di equilibrio si avrà:
sono le differenze/i gradienti della concentrazione di massa, le forze che consentono l'assorbimento o il discioglimento e l'emissione dei gas non condensabili. Indica che il trasporto del gas non condensabile tra le due fasi richiede una partenza di concentrazione di massa dal suo stato di equilibrio. La direzione del trasferimento di massa sposta il sistema verso equilibrio in base alle concentrazioni di massa locale e in equilibrio in entrambe le fasi. Dal modello di equilibrio si avrà:◦ Assorbimento/discioglimento del gas in un liquido - Il trasferimento della massa ha luogo a partire dalla fase gassosa (gas libero) alla fase liquida (gas disciolto). Il modello di equilibrio presuppone che il gas libero nella fase gassosa sia in uno stato di equilibrio: 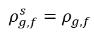 . Utilizzando l'equazione 2.204 e l'equazione 2.209, si avrà:
. Utilizzando l'equazione 2.204 e l'equazione 2.209, si avrà:
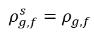 . Utilizzando l'equazione 2.204 e l'equazione 2.209, si avrà:
. Utilizzando l'equazione 2.204 e l'equazione 2.209, si avrà: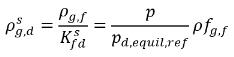
equazione 2.210
Dall'equazione 2.202 e l'equazione 2.203, i termini di origine del trasferimento della massa sono:
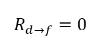
equazione 2.211
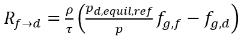
equazione 2.212
◦ Emissione di gas da un liquido - Il trasferimento della massa ha luogo a partire dalla fase liquida (gas disciolto) alla fase gassosa (gas libero). Durante questo processo, il modello di equilibrio assume che il gas disciolto nella fase liquida sia sempre nello stato di equilibrio: 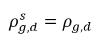 . Dall'equazione 2.202, l'equazione 2.203, l'equazione 2.204 e l'equazione 2.209, le velocità di trasferimento della massa sono:
. Dall'equazione 2.202, l'equazione 2.203, l'equazione 2.204 e l'equazione 2.209, le velocità di trasferimento della massa sono:
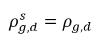 . Dall'equazione 2.202, l'equazione 2.203, l'equazione 2.204 e l'equazione 2.209, le velocità di trasferimento della massa sono:
. Dall'equazione 2.202, l'equazione 2.203, l'equazione 2.204 e l'equazione 2.209, le velocità di trasferimento della massa sono: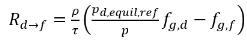
equazione 2.213
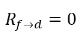
equazione 2.214
Quando una parte del gas non condensabile viene disciolta nel liquido, il gas che si espande liberamente è l'unica parte che rimane nella fase gassosa, il fg,f. Pertanto, la densità della miscela viene calcolata come:
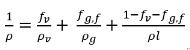
equazione 2.215
e la frazione di volume del gas libero è:
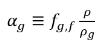
equazione 2.216