Modello di particelle distinte
Nel modello di particelle distinte, il flusso della fase dispersa viene modellato tenendo traccia di un numero specificato di particelle attraverso la fase del fluido continuo. In Creo Flow Analysis, il modello si basa sui presupposti e le restrizioni descritti di seguito.
• Numero definito di particelle sferiche attraverso la fase di flusso del fluido continuo. Le particelle vengono definite come Con massa (Has Mass) o Senza massa (Massless).
• Un raggio specificato in corrispondenza della posizione e dell'ora di rilascio determina la dimensione della particella, che rimane invariata. L'interazione particella-particella è trascurabile.
• Le particelle interagiscono con il flusso del fluido e i limiti della parete. Il volume di una particella non sposta alcun fluido (frazioni di volume basso nella fase della particella) e non interferisce con la geometria (una particella sovramisura si adatta a uno spazio più piccolo).
• Non viene eseguito alcun trasferimento di calore e di massa tra la fase del fluido continuo e le particelle. Si presuppone che la temperatura delle particelle sia uguale alla temperatura locale del flusso del fluido.
Con questi presupposti, il movimento di ogni singola particella viene tracciato utilizzando l'approccio lagrangiano. Il monitoraggio viene eseguito formando un insieme di equazioni differenziali ordinarie nel tempo per ciascuna particella, costituito da equazioni per posizione e velocità. Queste equazioni vengono quindi integrate per calcolare la reazione delle particelle mentre attraversano il dominio di flusso. Di seguito sono riportate le caratteristiche dell'approccio della modellazione delle particelle in Creo Flow Analysis.
• Il modello di particella discreta segue l'approccio di Eulero-Lagrange. La fase del fluido viene gestita come un continuum risolvendo la continuità e le equazioni di Navier-Stokes. La fase dispersa viene risolta tracciando il movimento di ogni singola particella secondo l'approccio lagrangiano. La frazione di volume assunta dalle particelle non viene inclusa nel calcolo della fase continua.
• Le particelle impostate su Senza massa (Massless) si spostano con il flusso del fluido e seguono le linee di flusso del campo di flusso. La dimensione o il raggio delle particelle non influisce sul flusso o sulle particelle ed è utile solo per la visualizzazione.
• Per le particelle impostate su Con massa (Has Mass), la massa è determinata dai valori che si specificano per il raggio o il diametro e la densità specificati delle particelle. Le forze che agiscono su una particella, che ne determinano il movimento, includono il trascinamento del fluido particellare (forza inerziale) e la gravità. Le forze di dispersione di turbolenza sulle particelle non vengono considerate. La dimensione delle particelle influenza le forze di trascinamento del fluido particellare e la postelaborazione.
• Lo scambio di momento tra la fase del fluido e le fasi delle particelle distinte è modellato dai principi descritti di seguito.
◦ Accoppiamento unidirezionale - Solo la fase del fluido influisce sui movimenti delle particelle.
◦ Accoppiamento bidirezionale - Anche le particelle influenzano il flusso del fluido attraverso forze di trascinamento del fluido particellare.
• Le interazioni parete-particella vengono modellate utilizzando modelli particella-parete quali aderenza, rimbalzo perfetto e rimbalzo parziale.
• Sebbene la fase del fluido possa essere costante e instabile, il monitoraggio delle particelle è un processo transitorio che implica l'integrazione di percorsi di particelle attraverso il dominio discretizzato. In questo approccio, singole particelle vengono rilasciate o iniettate da posizioni specificate in momenti diversi. Ogni particella viene tracciata dalla posizione di rilascio alla destinazione, dove sfugge al dominio o soddisfa determinati limiti di integrazione. Infine, viene ottenuta una media di tutte le tracce delle particelle e le interazioni fluido-particella vengono calcolate come termini di origine per le equazioni del momento della fase del fluido.
• Il percorso seguito dalle particelle viene visualizzato utilizzando il metodo di monitoraggio della linea fluida nel modulo Particella (Particle).
Teoria del movimento delle particelle
Nell'approccio di Lagrange, il movimento di una particella è determinato dall'equilibrio delle forze sulla particella e dalle condizioni in cui la particella viene rilasciata (condizioni iniziali). Per modellare la fase di particella distinta, vengono prima di tutto formate le equazioni di movimento per le particelle in base all'equilibrio delle forze. Successivamente si possono specificare le condizioni iniziali e al limite per le particelle. Infine, viene eseguita l'integrazione dell'equazione di movimento delle particelle per tracciare le particelle.
Equazioni di movimento per le particelle
• Equilibrio delle forze delle particelle
Per una particella distinta che viaggia in un mezzo fluido continuo, il movimento è determinato dalla forza netta che agisce su di essa. In base alla seconda legge di Newton, si può esprimere l'equilibrio delle forze sulla particella nell'equazione di Lagrange seguente:
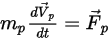
Equazione 2.366
dove
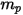 | massa particella in kg |
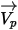 | velocità particella in m/s |
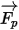 | forza netta esercitata sulla particella (N), che influisce sull'accelerazione della particella |
In un sistema di coordinate cartesiano, se
punto 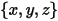 | posizione della particella |
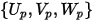 | componenti della velocità della particella |
Con l'approccio lagrangiano la velocità della particella 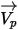 viene definita nel modo seguente:
viene definita nel modo seguente:
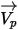 viene definita nel modo seguente:
viene definita nel modo seguente: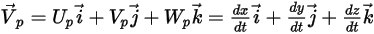
Equazione 2.367
Per una particella sferica che occupa un volume 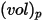 con densità
con densità 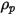 e diametro
e diametro 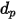 (Creo Flow Analysis accetta il raggio come input), la massa della particella
(Creo Flow Analysis accetta il raggio come input), la massa della particella 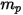 viene calcolata come segue:
viene calcolata come segue:
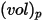 con densità
con densità 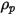 e diametro
e diametro 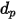 (Creo Flow Analysis accetta il raggio come input), la massa della particella
(Creo Flow Analysis accetta il raggio come input), la massa della particella 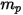 viene calcolata come segue:
viene calcolata come segue: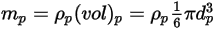
Equazione 2.368
Per quanto riguarda la forza netta 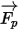 , i fattori contribuenti sono la forza di trascinamento fluido-particella, l'effetto di gravità e le forze dovute alla rotazione del dominio (forze centripeta e di Coriolis). Fattori contribuenti aggiuntivi sono altre forze dovute alla differenza di velocità tra la particella e il fluido e allo spostamento del fluido rispetto alla particella. In Creo Flow Analysis,
, i fattori contribuenti sono la forza di trascinamento fluido-particella, l'effetto di gravità e le forze dovute alla rotazione del dominio (forze centripeta e di Coriolis). Fattori contribuenti aggiuntivi sono altre forze dovute alla differenza di velocità tra la particella e il fluido e allo spostamento del fluido rispetto alla particella. In Creo Flow Analysis, 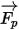 può essere espressa come segue:
può essere espressa come segue:
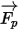 , i fattori contribuenti sono la forza di trascinamento fluido-particella, l'effetto di gravità e le forze dovute alla rotazione del dominio (forze centripeta e di Coriolis). Fattori contribuenti aggiuntivi sono altre forze dovute alla differenza di velocità tra la particella e il fluido e allo spostamento del fluido rispetto alla particella. In Creo Flow Analysis,
, i fattori contribuenti sono la forza di trascinamento fluido-particella, l'effetto di gravità e le forze dovute alla rotazione del dominio (forze centripeta e di Coriolis). Fattori contribuenti aggiuntivi sono altre forze dovute alla differenza di velocità tra la particella e il fluido e allo spostamento del fluido rispetto alla particella. In Creo Flow Analysis, 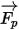 può essere espressa come segue:
può essere espressa come segue: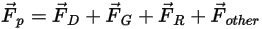
Equazione 2.369
dove
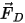 | forza di trascinamento (N) |
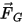 | forza gravitazionale (N) |
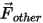 | altre forze come la forza di massa virtuale, la forza del gradiente di pressione, la forza di sollevamento specificata dall'utente (n) |
Per default, viene considerata solo la forza di trascinamento sulla particella.
Se si sostituisce l'equazione 2.369 con l'equazione 2.366 e la si divide per 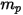 , l'equazione di equilibrio delle forze risolta per una particella si presenta nel seguente modo:
, l'equazione di equilibrio delle forze risolta per una particella si presenta nel seguente modo:
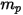 , l'equazione di equilibrio delle forze risolta per una particella si presenta nel seguente modo:
, l'equazione di equilibrio delle forze risolta per una particella si presenta nel seguente modo: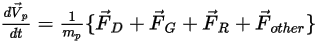
Equazione 2.370
Per chiudere l'equazione 2.370, è necessario calcolare il contributo di ogni singola forza. Di seguito sono indicati i sottomodelli o le formulazioni adottate in Creo Flow Analysis.
◦ Forza di trascinamento sulle particelle
La forza di trascinamento aerodinamica su una particella è proporzionale alla velocità di slittamento di fase, la differenza tra le velocità del fluido e della particella. Supponendo che nello stesso spazio in cui si trova la particella in un determinato momento, la velocità del flusso sia uguale a 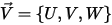 , la forza di trascinamento è espressa come:
, la forza di trascinamento è espressa come:
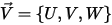 , la forza di trascinamento è espressa come:
, la forza di trascinamento è espressa come: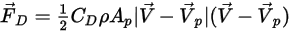
Equazione 2.371
dove
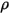 | densità della fase del fluido |
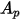 | area della particella proiettata nella direzione del flusso |
Per una particella sferica con diametro 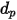 ,
, 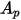 è l'area massima della sezione trasversale:
è l'area massima della sezione trasversale:
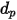 ,
, 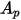 è l'area massima della sezione trasversale:
è l'area massima della sezione trasversale: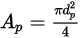
Equazione 2.372
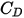 è il coefficiente di trascinamento, che dipende dal numero di Reynolds relativo
è il coefficiente di trascinamento, che dipende dal numero di Reynolds relativo 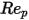 :
: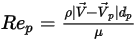
Equazione 2.373
dove 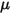 è la viscosità dinamica del fluido (PA-s).
è la viscosità dinamica del fluido (PA-s).
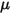 è la viscosità dinamica del fluido (PA-s).
è la viscosità dinamica del fluido (PA-s).Il coefficiente di trascinamento 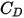 viene introdotto per tenere conto dei risultati sperimentali sul trascinamento viscoso di una sfera solida. Sono stati sviluppati vari modelli o correlazioni empiriche per determinare la funzione di trascinamento
viene introdotto per tenere conto dei risultati sperimentali sul trascinamento viscoso di una sfera solida. Sono stati sviluppati vari modelli o correlazioni empiriche per determinare la funzione di trascinamento 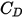 (
(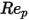 ) per stimare lo scambio fluido-particella. Per le particelle sferiche levigate, tra i molti modelli, la funzione
) per stimare lo scambio fluido-particella. Per le particelle sferiche levigate, tra i molti modelli, la funzione 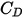 più completa è rappresentata dalle correzioni di Morsi e Alexander,
più completa è rappresentata dalle correzioni di Morsi e Alexander,
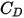 viene introdotto per tenere conto dei risultati sperimentali sul trascinamento viscoso di una sfera solida. Sono stati sviluppati vari modelli o correlazioni empiriche per determinare la funzione di trascinamento
viene introdotto per tenere conto dei risultati sperimentali sul trascinamento viscoso di una sfera solida. Sono stati sviluppati vari modelli o correlazioni empiriche per determinare la funzione di trascinamento 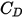 (
(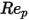 ) per stimare lo scambio fluido-particella. Per le particelle sferiche levigate, tra i molti modelli, la funzione
) per stimare lo scambio fluido-particella. Per le particelle sferiche levigate, tra i molti modelli, la funzione 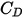 più completa è rappresentata dalle correzioni di Morsi e Alexander,
più completa è rappresentata dalle correzioni di Morsi e Alexander,Riferimenti: S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193-208, 26 settembre 1972.
che si esprime in generale come:
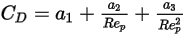
Equazione 2.374
dove 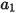 ,
, 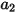 e
e 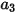 sono costanti di modello, i cui valori dipendono dal numero relativo di Reynolds, come mostrato nella tabella riportata di seguito.
sono costanti di modello, i cui valori dipendono dal numero relativo di Reynolds, come mostrato nella tabella riportata di seguito.
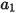 ,
, 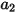 e
e 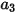 sono costanti di modello, i cui valori dipendono dal numero relativo di Reynolds, come mostrato nella tabella riportata di seguito.
sono costanti di modello, i cui valori dipendono dal numero relativo di Reynolds, come mostrato nella tabella riportata di seguito.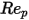 | 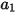 | 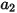 | 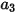 |
0 < 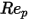 <=0.1 <=0.1 | 0 | 24 | 0 |
0.1 < 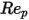 <=1 <=1 | 3.690 | 22.73 | 0.0903 |
1< 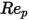 <=10 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 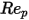 <=100 <=100 | 0.6167 | 46.50 | -116.67 |
100 < 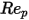 <=1000 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 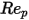 <=5000 <=5000 | 0.357 | 148.62 | -47500 |
5000 < 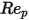 <=10000 <=10000 | 0.46 | -490.546 | 578700 |
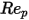 >10000 >10000 | 0.5191 | -1662.5 | 5416700 |
La tabella mostra che in presenza di numeri di Reynolds di particelle molto bassi (regime viscoso), 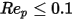 , il coefficiente di trascinamento per le particelle sferiche passate al fluido torna alla legge di Stokes:
, il coefficiente di trascinamento per le particelle sferiche passate al fluido torna alla legge di Stokes:
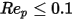 , il coefficiente di trascinamento per le particelle sferiche passate al fluido torna alla legge di Stokes:
, il coefficiente di trascinamento per le particelle sferiche passate al fluido torna alla legge di Stokes:
Equazione 2.375
Al contrario, quando 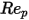 è sufficientemente grande da consentire agli effetti inerziali di dominare gli effetti viscosi, il flusso di fluido-particella si trova nel regime di Newton o inerziale. Dalla tabella si osserva che il coefficiente di trascinamento diventa meno dipendente dal numero di Reynolds relativo. Inoltre, viene spesso utilizzata una costante di valore
è sufficientemente grande da consentire agli effetti inerziali di dominare gli effetti viscosi, il flusso di fluido-particella si trova nel regime di Newton o inerziale. Dalla tabella si osserva che il coefficiente di trascinamento diventa meno dipendente dal numero di Reynolds relativo. Inoltre, viene spesso utilizzata una costante di valore 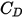 al posto del modello di Morsi e Alexander completo:
al posto del modello di Morsi e Alexander completo:
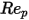 è sufficientemente grande da consentire agli effetti inerziali di dominare gli effetti viscosi, il flusso di fluido-particella si trova nel regime di Newton o inerziale. Dalla tabella si osserva che il coefficiente di trascinamento diventa meno dipendente dal numero di Reynolds relativo. Inoltre, viene spesso utilizzata una costante di valore
è sufficientemente grande da consentire agli effetti inerziali di dominare gli effetti viscosi, il flusso di fluido-particella si trova nel regime di Newton o inerziale. Dalla tabella si osserva che il coefficiente di trascinamento diventa meno dipendente dal numero di Reynolds relativo. Inoltre, viene spesso utilizzata una costante di valore 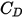 al posto del modello di Morsi e Alexander completo:
al posto del modello di Morsi e Alexander completo: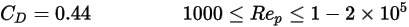
Equazione 2.376
Nella regione di transizione tra i regimi viscoso e inerziale, 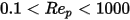 , per le particelle sferiche, sia gli effetti viscosi che quelli inerziali sono importanti. Di conseguenza, il coefficiente di trascinamento è una funzione complessa del numero di Reynolds relativo, che può essere stimato dal modello di Morsi e Alexander o da altre correlazioni. Ad esempio, secondo il modello di Schiller e Naumann:
, per le particelle sferiche, sia gli effetti viscosi che quelli inerziali sono importanti. Di conseguenza, il coefficiente di trascinamento è una funzione complessa del numero di Reynolds relativo, che può essere stimato dal modello di Morsi e Alexander o da altre correlazioni. Ad esempio, secondo il modello di Schiller e Naumann:
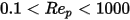 , per le particelle sferiche, sia gli effetti viscosi che quelli inerziali sono importanti. Di conseguenza, il coefficiente di trascinamento è una funzione complessa del numero di Reynolds relativo, che può essere stimato dal modello di Morsi e Alexander o da altre correlazioni. Ad esempio, secondo il modello di Schiller e Naumann:
, per le particelle sferiche, sia gli effetti viscosi che quelli inerziali sono importanti. Di conseguenza, il coefficiente di trascinamento è una funzione complessa del numero di Reynolds relativo, che può essere stimato dal modello di Morsi e Alexander o da altre correlazioni. Ad esempio, secondo il modello di Schiller e Naumann:Riferimenti: L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
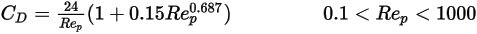
Equazione 2.377
Per semplificare l'espressione del termine di forza di trascinamento nell'equazione 2.370, viene introdotto il tempo di rilassamento del particolato 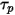 :
:
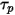 :
: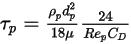
Equazione 2.378
Se si combinano l'equazione 2.368, l'equazione 2.371, l'equazione 2.372, l'equazione 2.373 e l'equazione 2.378, la forza di trascinamento per unità di massa di particelle presenta la formulazione seguente:
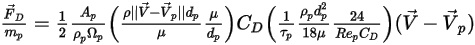
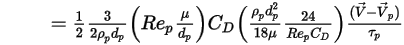
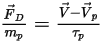
Equazione 2.379
Di conseguenza, l'equazione per l'equilibrio delle forze delle particelle di default (viene considerata solo la forza di trascinamento) si esprime come:
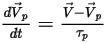
Equazione 2.380
• Aggiunta del termine di gravità
Per default, il termine di gravità non è incluso nell'equazione di equilibrio delle forze delle particelle, ma è possibile attivarlo in Creo Flow Analysis. Per una particella immersa nel flusso del fluido, l'effetto della gravità determina una forza di galleggiamento che è uguale al peso del fluido spostato dalla particella. Supponendo che 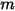 sia la massa di fluido spostata dalla particella e
sia la massa di fluido spostata dalla particella e 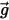 sia il vettore di gravità, la forza risultante viene formulata come:
sia il vettore di gravità, la forza risultante viene formulata come:
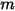 sia la massa di fluido spostata dalla particella e
sia la massa di fluido spostata dalla particella e 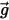 sia il vettore di gravità, la forza risultante viene formulata come:
sia il vettore di gravità, la forza risultante viene formulata come: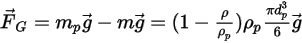
Equazione 2.381
In alternativa, la forza per unità di massa di particelle viene formulata come:
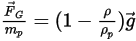
Equazione 2.382
E l'equazione di equilibrio delle forze viene espressa come:
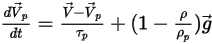
Equazione 2.383
• Forza di rotazione sulle particelle
Per i flussi di fluido modello in un frame di riferimento in rotazione, il termine di forza supplementare indotto dalla rotazione 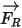 è una parte intrinseca dell'accelerazione della particella. È costituito dall'effetto delle forze centripeta e di Coriolis:
è una parte intrinseca dell'accelerazione della particella. È costituito dall'effetto delle forze centripeta e di Coriolis:
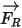 è una parte intrinseca dell'accelerazione della particella. È costituito dall'effetto delle forze centripeta e di Coriolis:
è una parte intrinseca dell'accelerazione della particella. È costituito dall'effetto delle forze centripeta e di Coriolis: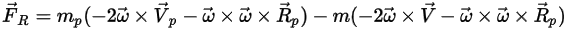
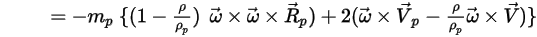
Equazione 2.384
In alternativa, la forza di rotazione per unità di massa di particelle viene espressa come:
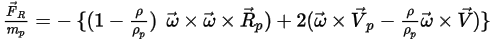
Equazione 2.385
dove
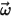 | velocità angolare del frame di riferimento in rotazione |
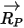 | vettore che collega il centro dell'asse e la posizione della particella |
Con l'aggiunta di questo termine di forza, l'equazione di equilibrio delle particelle è:
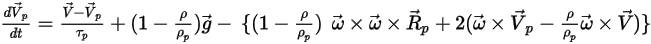
Equazione 2.386
L'equazione 2.386 governa il movimento di una particella in un sistema di Lagrange quando il flusso viene risolto in un frame di riferimento in rotazione.
Condizioni iniziali e al limite per le particelle
Nell'approccio di Lagrange, il monitoraggio delle particelle è una procedura transitoria. Pertanto, sono necessarie le condizioni iniziali e al limite per calcolare le traiettorie delle particelle. Le condizioni al limite definiscono la reazione delle particelle ai limiti del dominio di calcolo, in particolare delle interazioni particella-parete. Le condizioni iniziali determinano il rilascio di particelle da limiti, tra cui la posizione di rilascio, la frequenza, la velocità, il tipo e la dimensione (raggio) della particella e il numero di particelle.
Condizioni al limite
Creo Flow Analysis fornisce una condizione al limite di fase distinta per determinare la reazione delle particelle in corrispondenza di un limite. Quando una particella raggiunge un limite del dominio di flusso (compreso il limite fisico e l'interfaccia solido-fluido), ad esempio una parete o un limite di ingresso, si verifica una delle situazioni descritte di seguito.
• La particella si riflette attraverso una collisione elastica o anelastica.
• La particella fuoriesce dal limite e viene persa dal calcolo in corrispondenza del punto di impatto con il limite.
• La particella viene intrappolata nella parete e viene persa dal calcolo in corrispondenza del punto di impatto con il limite.
• La particella attraversa una zona limite interna, ad esempio una ventola o un salto poroso.
• L'interazione particella-limite è determinata da metodi definiti dall'utente per modellare la reazione della particella quando colpisce il limite.
In base alla reazione della particella ai limiti, le condizioni al limite e le interfacce del flusso vengono raggruppate in tre tipi di condizioni al limite di particella distinta: aperta, simmetria e parete.
• Limite aperto della particella distinta
Le particelle o le linee di flusso possono uscire dal dominio di calcolo. Un limite aperto è un limite di entrata o di uscita della fase di flusso del fluido nel sistema di Eulero. Può inoltre essere applicato a limiti di flusso quali il limite di parete e di simmetria. A un limite di particella aperto, la particella esce o entra nel dominio a seconda della direzione della velocità della particella.
Si consideri 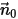 come l'unità di vettore normale al limite aperto che punta nella direzione opposta al dominio di calcolo, con la velocità al limite della particella
come l'unità di vettore normale al limite aperto che punta nella direzione opposta al dominio di calcolo, con la velocità al limite della particella 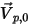 . Se
. Se 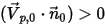 , il vettore di velocità
, il vettore di velocità 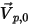 punta lontano dal dominio di calcolo. Ciò indica che la particella fuoriesce dal limite e viene persa dal calcolo in corrispondenza del punto di impatto con il limite.
punta lontano dal dominio di calcolo. Ciò indica che la particella fuoriesce dal limite e viene persa dal calcolo in corrispondenza del punto di impatto con il limite.
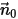 come l'unità di vettore normale al limite aperto che punta nella direzione opposta al dominio di calcolo, con la velocità al limite della particella
come l'unità di vettore normale al limite aperto che punta nella direzione opposta al dominio di calcolo, con la velocità al limite della particella 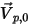 . Se
. Se 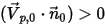 , il vettore di velocità
, il vettore di velocità 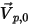 punta lontano dal dominio di calcolo. Ciò indica che la particella fuoriesce dal limite e viene persa dal calcolo in corrispondenza del punto di impatto con il limite.
punta lontano dal dominio di calcolo. Ciò indica che la particella fuoriesce dal limite e viene persa dal calcolo in corrispondenza del punto di impatto con il limite.• Limite di simmetria della particella
Quando una particella o una linea fluida nel dominio di calcolo colpisce un limite di simmetria distinto, la condizione al limite la riflette nuovamente nel dominio. Per la fase di particella distinta, un limite di particella di simmetria corrisponde in genere a una simmetria di flusso nel sistema di Eulero. Può anche essere una posizione per il rilascio di particelle.
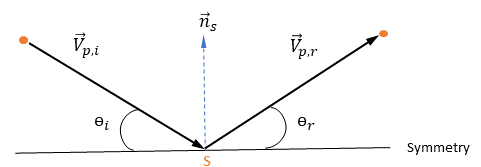
Si consideri 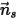 come l'unità di vettore normale a simmetria al punto
come l'unità di vettore normale a simmetria al punto 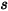 della simmetria, con la direzione che punta lontano dalla simmetria al dominio di calcolo. Vengono introdotti
della simmetria, con la direzione che punta lontano dalla simmetria al dominio di calcolo. Vengono introdotti 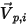 e
e 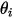 per indicare l'angolo di velocità di impatto della particella in corrispondenza del limite di simmetria della particella, come mostrato nell'illustrazione riportata di seguito. Quando la particella si riflette lontano dalla simmetria, ne viene conservata l'energia cinetica totale: la velocità tangenziale rimane invariata, mentre la componente velocità normale cambia solo il segno. La condizione al limite della simmetria della particella viene espressa come:
per indicare l'angolo di velocità di impatto della particella in corrispondenza del limite di simmetria della particella, come mostrato nell'illustrazione riportata di seguito. Quando la particella si riflette lontano dalla simmetria, ne viene conservata l'energia cinetica totale: la velocità tangenziale rimane invariata, mentre la componente velocità normale cambia solo il segno. La condizione al limite della simmetria della particella viene espressa come:
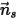 come l'unità di vettore normale a simmetria al punto
come l'unità di vettore normale a simmetria al punto 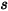 della simmetria, con la direzione che punta lontano dalla simmetria al dominio di calcolo. Vengono introdotti
della simmetria, con la direzione che punta lontano dalla simmetria al dominio di calcolo. Vengono introdotti 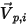 e
e 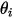 per indicare l'angolo di velocità di impatto della particella in corrispondenza del limite di simmetria della particella, come mostrato nell'illustrazione riportata di seguito. Quando la particella si riflette lontano dalla simmetria, ne viene conservata l'energia cinetica totale: la velocità tangenziale rimane invariata, mentre la componente velocità normale cambia solo il segno. La condizione al limite della simmetria della particella viene espressa come:
per indicare l'angolo di velocità di impatto della particella in corrispondenza del limite di simmetria della particella, come mostrato nell'illustrazione riportata di seguito. Quando la particella si riflette lontano dalla simmetria, ne viene conservata l'energia cinetica totale: la velocità tangenziale rimane invariata, mentre la componente velocità normale cambia solo il segno. La condizione al limite della simmetria della particella viene espressa come: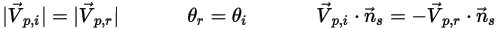
Equazione 2.387
dove
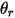 | angolo in corrispondenza del punto 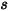 : della simmetria (grado) : della simmetria (grado) |
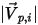 | ampiezza della velocità incidente della particella (m/s) |
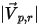 | ampiezza della velocità riflessa della particella (m/s) |
• Limite di parete della particella
Per le gocce liquide, l'interazione goccia-parete dipende dalla temperatura della parete, dal materiale della parete e dalla rugosità, dall'angolo di impatto e dalla velocità di impatto, dall'esistenza di una pellicola sulla parete e da vari altri parametri. Di conseguenza, viene utilizzato un intervallo di sottomodelli per riprodurre i diversi regimi di interazioni parete-particella e per tenere conto degli impatti dei parametri di flusso e delle condizioni al limite di parete.
Nel modello di particella distinta corrente si presuppone che la forma, la dimensione e la massa delle particelle rimangano invariate. Inoltre, si considera che il fluido e le particelle siano in equilibrio termico. Pertanto, un approccio semplice descrive il processo di particelle (con massa) che collidono con le pareti: durante il processo di collisione, le particelle scambiano il momento solo con la parete e interagiscono con la parete in uno dei tre modi possibili. I tre modi sono il rimbalzo perfetto, l'aderenza e il rimbalzo parziale.
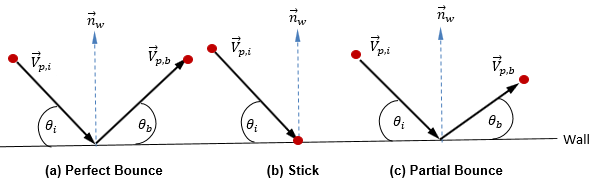
◦ Rimbalzo perfetto - Una particella o una linea fluida si riflette quando colpisce una parete. Il momento e l'energia cinetica della particella sono perfettamente conservati. L'angolo di incidenza è uguale all'angolo di riflessione, mentre il segno della componente velocità normale della parete cambia:
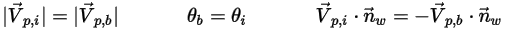
Equazione 2.388
dove
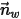 | unità di vettore normale di parete |
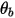 | angolo al limite della parete (grado) |
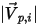 | ampiezza della velocità incidente della particella (m/s) |
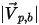 | ampiezza della velocità di rimbalzo della particella (m/s) |
◦ Aderenza - Una particella collide con la parete, perde tutto il momento e l'energia e si attacca alla parete:
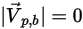
Senza considerare l'accumulo di particelle lungo la parete, la particella viene completamente persa dal calcolo in corrispondenza del punto di impatto con il limite.
◦ Rimbalzo parziale - Condizione di particella alla parete tra il rimbalzo perfetto e l'aderenza. Una particella o una linea fluida rimbalza da una parete ma perde parte dell'energia in una direzione normale, tangenziale o sia normale che tangenziale. Il momento e l'energia cinetica della particella non vengono conservati e l'angolo di incidenza è in genere maggiore dell'angolo di riflessione:
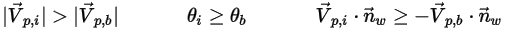
La perdita di energia attraverso l'interazione particella-parete viene specificata dagli input utente.
▪ Perdita di energia normale - Specifica la perdita della componente normale dell'energia cinetica di una particella all'impatto con la parete.
▪ Perdita di energia tangenziale - Specifica la perdita della componente tangenziale di energia cinetica di una particella all'impatto con la parete.
In Creo Flow Analysis, il verificarsi del rimbalzo o dell'aderenza della particella è determinato dai valori specificati delle velocità normali massima e minima. Supponendo che 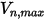 sia la velocità normale massima specificata della particella e che
sia la velocità normale massima specificata della particella e che 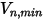 sia la velocità normale minima specificata, si verificano le condizioni descritte di seguito.
sia la velocità normale minima specificata, si verificano le condizioni descritte di seguito.
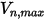 sia la velocità normale massima specificata della particella e che
sia la velocità normale massima specificata della particella e che 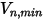 sia la velocità normale minima specificata, si verificano le condizioni descritte di seguito.
sia la velocità normale minima specificata, si verificano le condizioni descritte di seguito.▪ Se 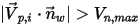 o
o 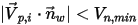 , la particella rimbalza dalla parete.
, la particella rimbalza dalla parete.
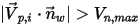 o
o 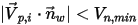 , la particella rimbalza dalla parete.
, la particella rimbalza dalla parete.▪ Se 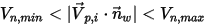 , la particella si attacca alla parete.
, la particella si attacca alla parete.
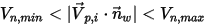 , la particella si attacca alla parete.
, la particella si attacca alla parete.I modelli di interazione particella-parete si applicano solo alle particelle con impostazione Con massa (Has Mass). Una particella senza massa segue la linea di flusso lungo le pareti.
I limiti di parete della particella possono essere pareti esterne e interfacce fluido-solido. Come nei limiti di particella aperto e di simmetria, le particelle possono essere rilasciate da un limite di parete.
Condizioni iniziali (rilascio di particelle)
Le condizioni iniziali forniscono i valori iniziali per tutte le variabili della fase distinta dipendenti che descrivono le condizioni istantanee di una singola particella. Per il monitoraggio delle particelle nel sistema di Lagrange, la procedura per determinare le condizioni iniziali implica rilasci di particelle (frequenza e distribuzioni) dai limiti (aperto, di simmetria, di parete e interfaccia) e l'assegnazione di proprietà per ciascuna particella.
Quando si attiva l'opzione Rilascia particella (Release Particle), i parametri o le variabili indicate di seguito sono le condizioni iniziali per i movimenti delle particelle.
Integrazione dell'equazione di movimento della particella
Per monitorare il movimento delle particelle, le equazioni di traiettoria di ciascuna particella vengono risolte (integrate) in modo analitico o numerico in un sistema di Lagrange. Partendo dall'equazione 2.367 e l'equazione 2.386, le equazioni di movimento si riscrivono come:
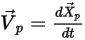
Equazione 2.391
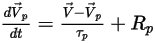
Equazione 2.392
dove
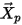 | vettore di posizione della particella |
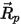 | include le accelerazioni dovute a tutte le altre forze come la gravità, gli effetti di rotazione e così via, eccetto la forza di trascinamento. |
L'equazione 2.391 e l'equazione 2.392 sono un set di equazioni differenziali ordinarie accoppiate. Con le condizioni iniziali e al limite specificate, lo spostamento della particella, equazione 2.391, viene calcolato utilizzando l'integrazione di incremento di Eulero della velocità della particella nel passo temporale, 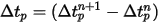 :
:
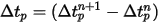 :
: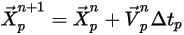
Equazione 2.393
dove
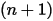 | nuovi valori |
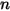 | valori correnti |
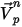 | velocità della particella al passo temporale corrente |
Al primo passo,
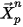 | posizione di rilascio |
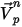 | velocità iniziale |
dove

Equazione 2.394
In questo metodo di integrazione di incremento, si presuppone che la velocità della particella calcolata all'inizio del passo temporale prevalga nell'intero passo. Alla fine del passo temporale, la nuova velocità della particella viene calcolata risolvendo l'equazione 2.392 del momento della particella. Supponendo che, 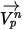
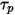 e
e 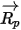 siano costanti nel periodo di tempo
siano costanti nel periodo di tempo 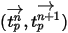 e che le proprietà del fluido siano ricavate dall'inizio del passo temporale al momento
e che le proprietà del fluido siano ricavate dall'inizio del passo temporale al momento 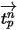 , si ha la soluzione analitica dell'equazione 2.392:
, si ha la soluzione analitica dell'equazione 2.392:
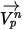
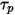 e
e 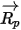 siano costanti nel periodo di tempo
siano costanti nel periodo di tempo 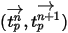 e che le proprietà del fluido siano ricavate dall'inizio del passo temporale al momento
e che le proprietà del fluido siano ricavate dall'inizio del passo temporale al momento 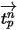 , si ha la soluzione analitica dell'equazione 2.392:
, si ha la soluzione analitica dell'equazione 2.392: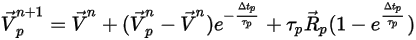
Equazione 2.395
Per valutare 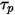 e
e 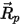 , sono necessarie variabili di fluido quali densità, viscosità e velocità in corrispondenza della posizione della particella. Queste variabili sono considerate valori di cella della fase del flusso del fluido in cui si trova attualmente la particella. Sebbene questo schema analitico sia efficiente, può diventare impreciso in caso di passi temporali ampi e in situazioni in cui le particelle non sono in equilibrio idrodinamico con il flusso del fluido continuo. In tale caso, gli schemi numerici integrano l' equazione 2.392.
, sono necessarie variabili di fluido quali densità, viscosità e velocità in corrispondenza della posizione della particella. Queste variabili sono considerate valori di cella della fase del flusso del fluido in cui si trova attualmente la particella. Sebbene questo schema analitico sia efficiente, può diventare impreciso in caso di passi temporali ampi e in situazioni in cui le particelle non sono in equilibrio idrodinamico con il flusso del fluido continuo. In tale caso, gli schemi numerici integrano l' equazione 2.392.
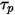 e
e 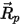 , sono necessarie variabili di fluido quali densità, viscosità e velocità in corrispondenza della posizione della particella. Queste variabili sono considerate valori di cella della fase del flusso del fluido in cui si trova attualmente la particella. Sebbene questo schema analitico sia efficiente, può diventare impreciso in caso di passi temporali ampi e in situazioni in cui le particelle non sono in equilibrio idrodinamico con il flusso del fluido continuo. In tale caso, gli schemi numerici integrano l' equazione 2.392.
, sono necessarie variabili di fluido quali densità, viscosità e velocità in corrispondenza della posizione della particella. Queste variabili sono considerate valori di cella della fase del flusso del fluido in cui si trova attualmente la particella. Sebbene questo schema analitico sia efficiente, può diventare impreciso in caso di passi temporali ampi e in situazioni in cui le particelle non sono in equilibrio idrodinamico con il flusso del fluido continuo. In tale caso, gli schemi numerici integrano l' equazione 2.392.Accoppiamento particella-fluido
Nell'approccio di Eulero-Lagrange si presuppone che il flusso del fluido continuo influisca sulla reazione delle particelle attraverso forze, calore e trasferimento di massa. Ad esempio, il termine di forza 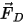 nell'equazione 2.370 dell'equilibrio delle forze della particella concerne la forza di trascinamento aerodinamica del flusso sulla particella. Sebbene la fase delle particelle sia considerata distinta e non sposti il fluido in termini di volume, le particelle possono esercitare un'influenza di contrasto sul flusso del fluido attraverso gli scambi di momento e possibilmente di massa e calore. L'effetto delle particelle sul flusso viene definito accoppiamento particella-fluido. Questo effetto si divide nelle due categorie descritte di seguito.
nell'equazione 2.370 dell'equilibrio delle forze della particella concerne la forza di trascinamento aerodinamica del flusso sulla particella. Sebbene la fase delle particelle sia considerata distinta e non sposti il fluido in termini di volume, le particelle possono esercitare un'influenza di contrasto sul flusso del fluido attraverso gli scambi di momento e possibilmente di massa e calore. L'effetto delle particelle sul flusso viene definito accoppiamento particella-fluido. Questo effetto si divide nelle due categorie descritte di seguito.
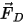 nell'equazione 2.370 dell'equilibrio delle forze della particella concerne la forza di trascinamento aerodinamica del flusso sulla particella. Sebbene la fase delle particelle sia considerata distinta e non sposti il fluido in termini di volume, le particelle possono esercitare un'influenza di contrasto sul flusso del fluido attraverso gli scambi di momento e possibilmente di massa e calore. L'effetto delle particelle sul flusso viene definito accoppiamento particella-fluido. Questo effetto si divide nelle due categorie descritte di seguito.
nell'equazione 2.370 dell'equilibrio delle forze della particella concerne la forza di trascinamento aerodinamica del flusso sulla particella. Sebbene la fase delle particelle sia considerata distinta e non sposti il fluido in termini di volume, le particelle possono esercitare un'influenza di contrasto sul flusso del fluido attraverso gli scambi di momento e possibilmente di massa e calore. L'effetto delle particelle sul flusso viene definito accoppiamento particella-fluido. Questo effetto si divide nelle due categorie descritte di seguito.• Accoppiamento unidirezionale
L'accoppiamento unidirezionale consente al fluido di influenzare le traiettorie delle particelle, ma le particelle non hanno alcun effetto sul fluido. Per le particelle senza massa, l'interazione particella-fluido è un accoppiamento unidirezionale, in quanto le particelle si spostano insieme al flusso del fluido. Per le particelle con massa, l'accoppiamento unidirezionale può essere un'approssimazione accettabile in flussi con carichi di fase dispersa bassi in cui le particelle hanno un'influenza trascurabile sul flusso del fluido.
Per la fase del fluido continuo, il campo di flusso viene calcolato come flusso di fluido monofase senza l'esistenza di una fase di particelle disperse. Il movimento delle particelle viene quindi tracciato in base al campo di flusso calcolato e alle condizioni iniziali. Per un flusso con stato stazionario, il tracciamento delle particelle si verifica dopo che la soluzione del flusso convergente della fase continua è stata ottenuta risolvendo la continuità e le equazioni di Navier-Stokes. Per una simulazione di flusso transitorio, i movimenti delle particelle vengono tracciati alla fine di ogni passo temporale della simulazione di flusso.
• Accoppiamento bidirezionale
Per le particelle con massa, l'accoppiamento bidirezionale consente al fluido di influenzare le traiettorie delle particelle. Inoltre, tiene in considerazione l'effetto delle particelle sulla fase del fluido continuo. Senza l'aggiunta del trasferimento di massa e di calore, l'interazione a doppio senso tra il fluido e le particelle riguarda solo lo scambio di momento. Per il momento trasferito dalla fase continua alla fase distinta, viene calcolato tracciando il momento acquisito o perso da ogni singola particella mentre passa attraverso un volume di controllo. Nell'accoppiamento bidirezionale, gli scambi di momento di particella-fluido devono essere inclusi nelle equazioni del momento fluido per tenere conto dell'effetto delle traiettorie della fase distinta sul continuum. Partendo dall'equazione 2.386, solo la forza di trascinamento tiene conto dello scambio di momento particella-fluido e viene aggiunta nelle equazioni del momento. Per le particelle senza massa, non viene calcolato alcun termine di interscambio con il flusso del fluido, pertanto le traiettorie della fase distinta non hanno alcun impatto sul continuum.
Per includere gli effetti di trascinamento particella-fluido nelle equazioni del momento della fase continua, la forza di trascinamento per ciascuna particella che si sposta attraverso il flusso viene applicata nel volume di controllo in cui si trova la particella durante il passo temporale. Per la particella 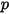 , si calcola l'origine del momento dovuta al trascinamento
, si calcola l'origine del momento dovuta al trascinamento 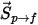 dalla seguente equazione differenziale:
dalla seguente equazione differenziale:
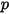 , si calcola l'origine del momento dovuta al trascinamento
, si calcola l'origine del momento dovuta al trascinamento 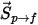 dalla seguente equazione differenziale:
dalla seguente equazione differenziale: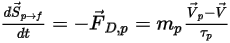
Equazione 2.396
Inoltre, l'origine della particella alla fase continua è il termine di origine 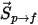 che si moltiplica per la velocità di flusso numerica per la particella (la portata nell'unità di tempo diviso la massa della particella):
che si moltiplica per la velocità di flusso numerica per la particella (la portata nell'unità di tempo diviso la massa della particella):
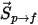 che si moltiplica per la velocità di flusso numerica per la particella (la portata nell'unità di tempo diviso la massa della particella):
che si moltiplica per la velocità di flusso numerica per la particella (la portata nell'unità di tempo diviso la massa della particella):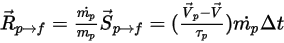
Equazione 2.397
dove
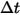 | passo temporale |
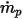 | portata nell'unità di tempo della particella |
Supponendo che 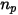 sia il numero di particelle che passano attraverso un volume di controllo durante il passo temporale
sia il numero di particelle che passano attraverso un volume di controllo durante il passo temporale 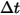 , si ha il termine di origine da particella a fluido totale:
, si ha il termine di origine da particella a fluido totale:
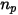 sia il numero di particelle che passano attraverso un volume di controllo durante il passo temporale
sia il numero di particelle che passano attraverso un volume di controllo durante il passo temporale 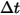 , si ha il termine di origine da particella a fluido totale:
, si ha il termine di origine da particella a fluido totale: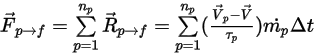
Equazione 2.398
Con l'aggiunta della forza di trascinamento particella-fluido, le equazioni di governo risolte per la fase continua sono espresse come:
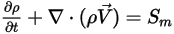
Equazione 2.399
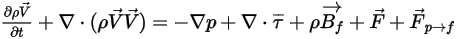
Equazione 2.400
Con un accoppiamento unidirezionale, 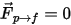 la fase del fluido continuo è regolata dalle equazioni esatte del momento e di continuità monofase. Per l'accoppiamento bidirezionale, è presente il termine di origine della forza di trascinamento da particella a fluido. L'equazione 2.399 e l'equazione 2.400 vengono risolte in modo identico al flusso monofase.
la fase del fluido continuo è regolata dalle equazioni esatte del momento e di continuità monofase. Per l'accoppiamento bidirezionale, è presente il termine di origine della forza di trascinamento da particella a fluido. L'equazione 2.399 e l'equazione 2.400 vengono risolte in modo identico al flusso monofase.
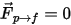 la fase del fluido continuo è regolata dalle equazioni esatte del momento e di continuità monofase. Per l'accoppiamento bidirezionale, è presente il termine di origine della forza di trascinamento da particella a fluido. L'equazione 2.399 e l'equazione 2.400 vengono risolte in modo identico al flusso monofase.
la fase del fluido continuo è regolata dalle equazioni esatte del momento e di continuità monofase. Per l'accoppiamento bidirezionale, è presente il termine di origine della forza di trascinamento da particella a fluido. L'equazione 2.399 e l'equazione 2.400 vengono risolte in modo identico al flusso monofase.