Caratteristiche di radiazione termica
Le caratteristiche di radiazione termica dipendono dalle proprietà dell'oggetto o del corpo emittente indicate di seguito:
• Temperatura della superficie
• Levigatezza o rugosità della superficie
• Coefficiente di assorbimento spettrale
• Potere emissivo spettrale
Come le onde elettromagnetiche, la radiazione termica è costituita da una dispersione continua di energie fotoniche con uno spettro di frequenze o lunghezze d'onda. Per un corpo emittente, la distribuzione dello spettro, il valore di picco della lunghezza d'onda e la quantità irradiata totale di tutte le lunghezze d'onda variano con la temperatura della superficie del corpo emittente. A loro volta, a una determinata temperatura della superficie, il coefficiente di assorbimento, la riflettività e l'emissività del corpo emittente sono tutti dipendenti dalla lunghezza d'onda della radiazione.
Interscambio di energia radiativa
Tutti i corpi irradiano energia sotto forma di fotoni che si muovono in una direzione casuale, con fase e frequenza casuali. Quando i fotoni irradiati dalla superficie di un corpo raggiungono la superficie di un altro corpo, come mostrato nell'illustrazione 2.35, possono essere assorbiti, riflessi e/o trasmessi. Il comportamento di una superficie con incidente di radiazione può essere descritto dalle quantità riportate di seguito.
Riferimenti: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
• Coefficiente di assorbimento α - Frazione di una radiazione incidente assorbita da una determinata lunghezza d'onda.
• Riflettività ρ - Frazione di una radiazione incidente riflessa a una determinata lunghezza d'onda.
• Trasmittanza τ - Frazione di una radiazione incidente trasmessa a una determinata lunghezza d'onda.
I tre coefficienti sono funzioni della lunghezza d'onda delle onde elettromagnetiche nella radiazione λ. Dal punto di vista dell'energia, devono essere sommati all'unità:
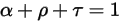
equazione 2.273
Secondo la legge di Kirchhoff sulla radiazione termica, l'emissività di un corpo emittente è uguale al coefficiente di assorbimento spettrale per qualsiasi lunghezza d'onda specificata, a causa della reciprocità:
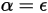
equazione 2.274
dove ε è l'emissività, il rapporto tra l'energia irradiata da un corpo emittente e quella di un emettitore perfetto (corpo nero) a pari temperatura e lunghezza d'onda.
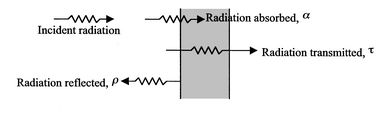
Illustrazione 2.35
L'equazione 2.273 indica che il modo in cui un corpo reagisce alla radiazione termica è caratterizzato dai relativi assorbimento α, riflessione ρ e trasmissione τ. A seconda dei valori di α, ρ e τ vengono definiti i tipi idealizzati del corpo di emissione descritti di seguito.
R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• Corpo opaco - Non trasmette alcuna radiazione che lo raggiunge, ma può riflettere una frazione di radiazione. τ=0 e α+ρ=1
• Corpo trasparente - Trasmette tutta la radiazione che lo raggiunge. τ=1 e α=ρ=0
• Corpo nero - Modello teorico proposto da Planck. Il corpo nero è un oggetto che assorbe tutta la radiazione elettromagnetica incidente a tutte le lunghezze d'onda, indipendentemente dalla frequenza o dall'angolo di incidenza. Se un oggetto emittente radiazioni conserva le caratteristiche fisiche di un corpo nero in equilibrio termodinamico, la radiazione viene chiamata radiazione di corpo nero. Per un corpo nero, α=ε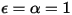 e
e 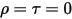
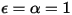 e
e 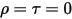
• Corpo bianco - Si presume che rifletta tutti i raggi incidenti in modo completo e uniforme in tutte le direzioni. 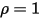 e
e 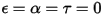
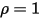 e
e 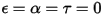
• Corpo grigio - Un corpo per cui 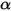 e
e 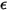 sono indipendenti dalla temperatura e dalla lunghezza d'onda.
sono indipendenti dalla temperatura e dalla lunghezza d'onda.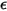 è uniforme per tutte le lunghezze d'onda. La radiazione da un corpo grigio o una superficie grigia è detta radiazione di corpo grigio. A differenza della radiazione di corpo grigio, la radiazione termica con uno spettro di lunghezze d'onda viene definita radiazione di corpo non grigio.
è uniforme per tutte le lunghezze d'onda. La radiazione da un corpo grigio o una superficie grigia è detta radiazione di corpo grigio. A differenza della radiazione di corpo grigio, la radiazione termica con uno spettro di lunghezze d'onda viene definita radiazione di corpo non grigio.
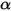 e
e 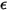 sono indipendenti dalla temperatura e dalla lunghezza d'onda.
sono indipendenti dalla temperatura e dalla lunghezza d'onda.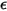 è uniforme per tutte le lunghezze d'onda. La radiazione da un corpo grigio o una superficie grigia è detta radiazione di corpo grigio. A differenza della radiazione di corpo grigio, la radiazione termica con uno spettro di lunghezze d'onda viene definita radiazione di corpo non grigio.
è uniforme per tutte le lunghezze d'onda. La radiazione da un corpo grigio o una superficie grigia è detta radiazione di corpo grigio. A differenza della radiazione di corpo grigio, la radiazione termica con uno spettro di lunghezze d'onda viene definita radiazione di corpo non grigio.Potenza radiativa
• Potenza 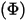 - Energia radiativa totale o netta emessa, riflessa, trasmessa o ricevuta per unità di tempo per una data origine.
- Energia radiativa totale o netta emessa, riflessa, trasmessa o ricevuta per unità di tempo per una data origine.
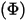 - Energia radiativa totale o netta emessa, riflessa, trasmessa o ricevuta per unità di tempo per una data origine.
- Energia radiativa totale o netta emessa, riflessa, trasmessa o ricevuta per unità di tempo per una data origine.• Irradiamento (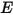 ) - Potenza di radiazione ricevuta da una superficie
) - Potenza di radiazione ricevuta da una superficie  per unità di area.
per unità di area. 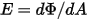
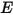 ) - Potenza di radiazione ricevuta da una superficie
) - Potenza di radiazione ricevuta da una superficie  per unità di area.
per unità di area. 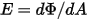
• Emittanza (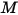 ) - Potenza di radiazione emessa
) - Potenza di radiazione emessa 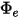 da una superficie per unità di area.
da una superficie per unità di area. 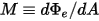
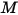 ) - Potenza di radiazione emessa
) - Potenza di radiazione emessa 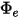 da una superficie per unità di area.
da una superficie per unità di area. 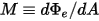
• Intensità (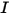 ) - Potenza irradiata in una determinata direzione (angolo solido
) - Potenza irradiata in una determinata direzione (angolo solido 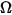 ), per una data origine.
), per una data origine. 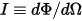
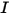 ) - Potenza irradiata in una determinata direzione (angolo solido
) - Potenza irradiata in una determinata direzione (angolo solido 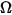 ), per una data origine.
), per una data origine. 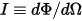
• Radiosità (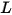 ) - Potenza radiante emessa, riflessa, trasmessa o ricevuta da una determinata superficie, per unità di angolo solido e per unità di area proiettata.
) - Potenza radiante emessa, riflessa, trasmessa o ricevuta da una determinata superficie, per unità di angolo solido e per unità di area proiettata. 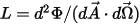
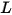 ) - Potenza radiante emessa, riflessa, trasmessa o ricevuta da una determinata superficie, per unità di angolo solido e per unità di area proiettata.
) - Potenza radiante emessa, riflessa, trasmessa o ricevuta da una determinata superficie, per unità di angolo solido e per unità di area proiettata. 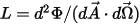
• Legge di Planck
La radiazione termica emessa da un corpo a qualsiasi temperatura è costituita da un'ampia gamma di frequenze. Per un corpo nero, la legge di Planck descrive la distribuzione delle frequenze della radiazione del corpo nero come solo la funzione della temperatura dell'oggetto. Planck ha dimostrato che la formulazione della radiosità spettrale di un corpo nero, 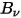 , definita come la potenza emessa per unità di area del corpo, per unità di angolo solido su cui viene misurata la radiazione e per unità di frequenza,
, definita come la potenza emessa per unità di area del corpo, per unità di angolo solido su cui viene misurata la radiazione e per unità di frequenza, 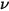 , è relativa alla temperatura del corpo:
, è relativa alla temperatura del corpo:
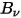 , definita come la potenza emessa per unità di area del corpo, per unità di angolo solido su cui viene misurata la radiazione e per unità di frequenza,
, definita come la potenza emessa per unità di area del corpo, per unità di angolo solido su cui viene misurata la radiazione e per unità di frequenza, 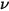 , è relativa alla temperatura del corpo:
, è relativa alla temperatura del corpo: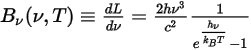
Equazione 2.275
dove
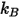 | Costante di Boltzmann |
h | Costante di Planck |
c | Velocità della luce nel vuoto o nel mezzo materiale |
La radiosità spettrale viene espressa anche per unità di lunghezza d'onda, λ:
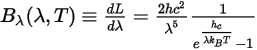
Equazione 2.276
• Legge di Stefan-Boltzmann:
Attraverso l'integrazione della legge di Planck sulla frequenza, v, l'output di potenza dato dalla legge di Stefan-Boltzmann è la potenza emessa da un corpo nero in termini di temperatura del corpo stesso. La legge di Stefan-Boltzmann è anche nota come emittanza radiante di un corpo nero. La legge di Stefan-Boltzmann enuncia che l'energia totale irradiata per unità di area di superficie di un corpo nero in tutte le lunghezze d'onda per unità di tempo è direttamente proporzionale alla quarta potenza della temperatura termodinamica del corpo nero. 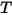 :
:
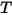 :
: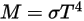
2.277
dove
σ | Costante di Stefan-Boltzmann |
M | Emittanza radiante |
Un corpo grigio, che non assorbe tutta la radiazione incidente, emette meno energia totale rispetto a un corpo nero. Con l'introduzione dell'emissività,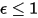 (corpo nero:
(corpo nero: 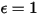 ), l' equazione 2.277 viene estesa a un corpo grigio:
), l' equazione 2.277 viene estesa a un corpo grigio:
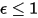 (corpo nero:
(corpo nero: 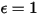 ), l' equazione 2.277 viene estesa a un corpo grigio:
), l' equazione 2.277 viene estesa a un corpo grigio: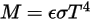
2.278
In base alla legge di Stefan-Boltzmann, la radiosità e la potenza emesse da un corpo vengono calcolate come segue:
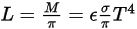
equazione 2.279
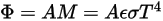
Equazione 2.280
• Legge di spostamento di Wien
La legge di Wien enuncia che la lunghezza d'onda λ, per cui la radiosità spettrale della radiazione di un corpo nero per unità di lunghezza d'onda raggiunge il suo valore di picco, è inversamente proporzionale alla temperatura:
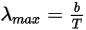
Equazione 2.281
dove b è la costante di spostamento di Wien.
Costanti di modello
Le costanti di modello utilizzate nei modelli teorici precedenti sono indicate nella tabella riportata di seguito.
h | Costante di Planck | 6.626 069 3(11) ×10-34J-s = 4.135 667 43(35) ×10-15eV-s |
b | Costante di spostamento di Wien | 2.897 768 5(51) ×10-3m-K |
kB | Costante di Boltzmann | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | Costante di Stefan-Boltzmann | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | Velocità della luce | 299.792.458 m/s |